题意简述:
输入 \(n\) 个棍子,输出最上面的棍子的编号。
向量叉积:

\(\bold{a}×\bold{b}=|\bold{a}|*|\bold{b}|*\sin\theta=S_{ABCO}=x1*y2-x2*y1\)
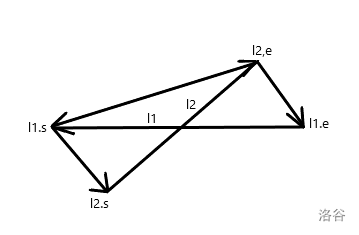
对于本题,首先我们要判断线段 \(l1\) 和 \(l2\) 所在的直线是否有交点。
代码如下(不懂的话可以自己手画一下):
max(l1.s.x,l1.e.x)>=min(l2.s.x,l2.e.x)&&max(l1.s.y,l1.e.y)>=min(l2.s.y,l2.e.y)//l1的端点在l2的两侧。
max(l2.s.x,l2.e.x)>=min(l1.s.x,l1.e.x)&&max(l2.s.y,l2.e.y)>=min(l1.s.y,l1.e.y)//l2的端点在l1的两侧。
然后,我们只需要用右手定则(右手定则:如果 \(\bold{a}\) 在 \(\bold{b}\) 的顺时针方向,那么 \(\bold{a}×\bold{b}=1\),否则 \(=0\)。)来判断的线段 \(l1\) 和 \(l2\) 的两个端点是否在另一条线段的两侧,这样就可以保证线段 \(l1\) 和 \(l2\) 有交点了。
如图,我们可以判断 \(sgn((l1.s,l2.s)×(l1.s,l1.e))*sgn((l1.s,l2.e)×(l1.s,l1.e))≤0\&\&sgn((12.e,l1.s)×(l2.e,l2.s))*sgn((l2.e,l1.e)×(l2.e,l2.s))≤0\)。
\((l1.s,l2.s)\) 表示向量 \(l1.s\) 到 \(l2.s\)。
我们可以重载 "\(-\)",使 \(l2.s-l1.s\) 表示 \((l1.s,l2.s)\)。
\(sgn(x)\) 返回 \(x\) 的正负性。
\(sgn(x)= \begin{cases} 1& \text{x>0}\0& \text{x=0}\-1& \text{x<0} \end{cases}\)
最后,我们发现答案不超过 \(1000\),所以直接暴力判断每个棍子即可。
#include<iostream>
#include<cstdio>
#include<cmath>
#define N 100010
#define eps 1e-8
#define pi acos(-1.0)
using namespace std;
int sgn(double x)
{
if(fabs(x)<eps) return 0;
if(x>0) return 1;
else return -1;
}
struct point
{
double x,y;
point(){}
point(double _x,double _y)
{
x=_x,y=_y;
}
point operator - (const point &b) const //向量(b.x,b.y)->(x,y)
{
return point(x-b.x,y-b.y);
}
double operator ^ (const point &b) const//(x,y)×(b.x,b.y)
{
return x*b.y-y*b.x;
}
double operator * (const point &b) const//(x,y)*(b.x,b.y)
{
return x*b.x+y*b.y;
}
};
struct Line
{
point s,e;//两个端点
Line(){}
Line(point _s,point _e)
{
s=_s,e=_e;
}
};
bool inter(Line l1,Line l2) //判断l1,l2是否有交点
{
return max(l1.s.x,l1.e.x)>=min(l2.s.x,l2.e.x)&&max(l1.s.y,l1.e.y)>=min(l2.s.y,l2.e.y)&&
max(l2.s.x,l2.e.x)>=min(l1.s.x,l1.e.x)&&max(l2.s.y,l2.e.y)>=min(l1.s.y,l1.e.y)&&
sgn((l2.e-l1.s)^(l1.e-l1.s))*sgn((l2.s-l1.s)^(l1.e-l1.s))<=0&&
sgn((l1.s-l2.e)^(l2.s-l2.e))*sgn((l1.e-l2.e)^(l2.s-l2.e))<=0;
}
Line line[N];
int flag[N];
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
if(!n) break;
double x1,y1,x2,y2;
for(int i=1; i<=n; i++)
{
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
line[i]=Line(point(x1,y1),point(x2,y2));
flag[i]=true;
}
for(int i=1; i<=n; i++)
for(int j=i+1; j<=n; j++)
if(inter(line[i],line[j]))
{
flag[i]=false;
break;
}
printf("Top sticks: ");
bool first=true;
for(int i=1; i<=n; i++)
{
if(flag[i])
{
if(first) first=false;
else printf(", ");
printf("%d",i);
}
}
printf(".\n");
}
return 0;
}
------------恢复内容开始------------
vjudge题目
题意简述:
输入 \(n\) 个棍子,输出最上面的棍子的编号。
向量叉积:

\(\bold{a}×\bold{b}=|\bold{a}|*|\bold{b}|*\sin\theta=S_{ABCO}=x1*y2-x2*y1\)

对于本题,首先我们要判断线段 \(l1\) 和 \(l2\) 所在的直线是否有交点。
代码如下(不懂的话可以自己手画一下):
max(l1.s.x,l1.e.x)>=min(l2.s.x,l2.e.x)&&max(l1.s.y,l1.e.y)>=min(l2.s.y,l2.e.y)//l1的端点在l2的两侧。
max(l2.s.x,l2.e.x)>=min(l1.s.x,l1.e.x)&&max(l2.s.y,l2.e.y)>=min(l1.s.y,l1.e.y)//l2的端点在l1的两侧。
然后,我们只需要用右手定则(右手定则:如果 \(\bold{a}\) 在 \(\bold{b}\) 的顺时针方向,那么 \(\bold{a}×\bold{b}=1\),否则 \(=0\)。)来判断的线段 \(l1\) 和 \(l2\) 的两个端点是否在另一条线段的两侧,这样就可以保证线段 \(l1\) 和 \(l2\) 有交点了。
如图,我们可以判断 \(sgn((l1.s,l2.s)×(l1.s,l1.e))*sgn((l1.s,l2.e)×(l1.s,l1.e))≤0\&\&sgn((12.e,l1.s)×(l2.e,l2.s))*sgn((l2.e,l1.e)×(l2.e,l2.s))≤0\)。
\((l1.s,l2.s)\) 表示向量 \(l1.s\) 到 \(l2.s\)。
我们可以重载 "\(-\)",使 \(l2.s-l1.s\) 表示 \((l1.s,l2.s)\)。
\(sgn(x)\) 返回 \(x\) 的正负性。
\(sgn(x)= \begin{cases} 1& \text{x>0}\0& \text{x=0}\-1& \text{x<0} \end{cases}\)
最后,我们发现答案不超过 \(1000\),所以直接暴力判断每个棍子即可。
#include<iostream>
#include<cstdio>
#include<cmath>
#define N 100010
#define eps 1e-8
#define pi acos(-1.0)
using namespace std;
int sgn(double x)
{
if(fabs(x)<eps) return 0;
if(x>0) return 1;
else return -1;
}
struct point
{
double x,y;
point(){}
point(double _x,double _y)
{
x=_x,y=_y;
}
point operator - (const point &b) const //向量(b.x,b.y)->(x,y)
{
return point(x-b.x,y-b.y);
}
double operator ^ (const point &b) const//(x,y)×(b.x,b.y)
{
return x*b.y-y*b.x;
}
double operator * (const point &b) const//(x,y)*(b.x,b.y)
{
return x*b.x+y*b.y;
}
};
struct Line
{
point s,e;//两个端点
Line(){}
Line(point _s,point _e)
{
s=_s,e=_e;
}
};
bool inter(Line l1,Line l2) //判断l1,l2是否有交点
{
return max(l1.s.x,l1.e.x)>=min(l2.s.x,l2.e.x)&&max(l1.s.y,l1.e.y)>=min(l2.s.y,l2.e.y)&&
max(l2.s.x,l2.e.x)>=min(l1.s.x,l1.e.x)&&max(l2.s.y,l2.e.y)>=min(l1.s.y,l1.e.y)&&
sgn((l2.e-l1.s)^(l1.e-l1.s))*sgn((l2.s-l1.s)^(l1.e-l1.s))<=0&&
sgn((l1.s-l2.e)^(l2.s-l2.e))*sgn((l1.e-l2.e)^(l2.s-l2.e))<=0;
}
Line line[N];
int flag[N];
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
if(!n) break;
double x1,y1,x2,y2;
for(int i=1; i<=n; i++)
{
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
line[i]=Line(point(x1,y1),point(x2,y2));
flag[i]=true;
}
for(int i=1; i<=n; i++)
for(int j=i+1; j<=n; j++)
if(inter(line[i],line[j]))
{
flag[i]=false;
break;
}
printf("Top sticks: ");
bool first=true;
for(int i=1; i<=n; i++)
{
if(flag[i])
{
if(first) first=false;
else printf(", ");
printf("%d",i);
}
}
printf(".\n");
}
return 0;
}
------------恢复内容结束------------
原文:https://www.cnblogs.com/Acestar/p/12961388.html