1035. Uncrossed Lines

We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw connecting lines: a straight line connecting two numbers A[i] and B[j] such that:

• A[i] == B[j];
• The line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.

Return the maximum number of connecting lines we can draw in this way.

Example 1:

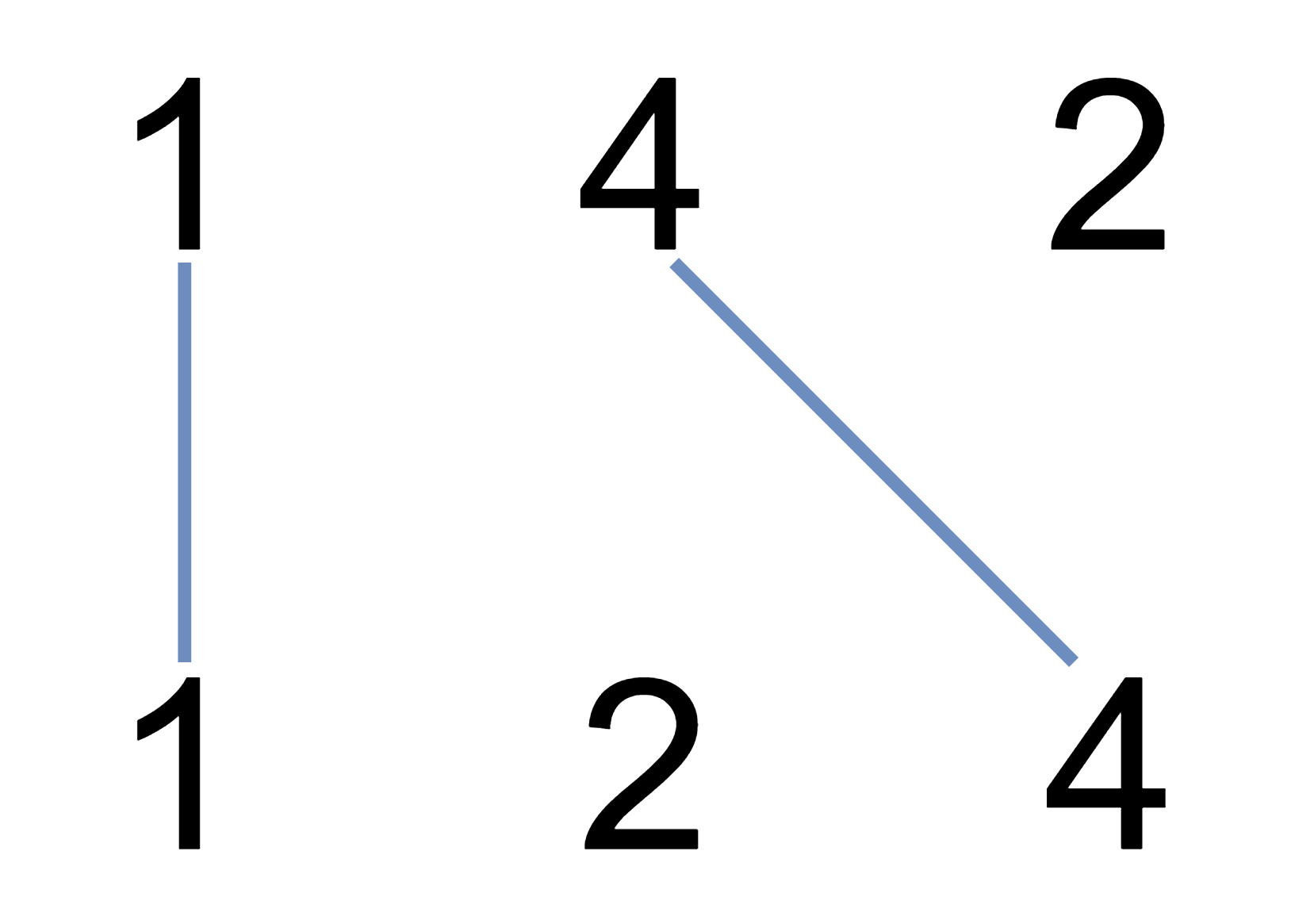
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

Note:

1. 1 <= A.length <= 500
2. 1 <= B.length <= 500
3. 1 <= A[i], B[i] <= 2000

class Solution {
  public int maxUncrossedLines(int[] A, int[] B) {
        int m = A.length, n = B.length, dp[][] = new int[m + 1][n + 1];
        for (int i = 1; i <= m; ++i)
            for (int j = 1; j <= n; ++j)
                if (A[i - 1] == B[j - 1])
                    dp[i][j] = 1 + dp[i - 1][j - 1];
                else
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
        return dp[m][n];
    }
}

Longest subsequence

1035. Uncrossed Lines

原文：https://www.cnblogs.com/wentiliangkaihua/p/12963054.html