题面

time limit per test: 2 seconds

memory limit per test: 256 megabytes

Description

There are two infinite sources of water:

• hot water of temperature h;
• cold water of temperature c (c<h).

You perform the following procedure of alternating moves:

1. take one cup of the hot water and pour it into an infinitely deep barrel;
2. take one cup of the cold water and pour it into an infinitely deep barrel;
3. take one cup of the hot water ……
4. and so on ……

Note that you always start with the cup of hot water.

The barrel is initially empty. You have to pour at least one cup into the barrel. The water temperature in the barrel is an average of the temperatures of the poured cups.

You want to achieve a temperature as close as possible to t. So if the temperature in the barrel is tb, then the absolute difference of tb and t (|tb?t|) should be as small as possible.

How many cups should you pour into the barrel, so that the temperature in it is as close as possible to t? If there are multiple answers with the minimum absolute difference, then print the smallest of them.

Input

The first line contains a single integer T (1≤T≤3?10⁴) — the number of testcases.

Each of the next T lines contains three integers h, c and t (1≤c<h≤10⁶; c≤t≤h) — the temperature of the hot water, the temperature of the cold water and the desired temperature in the barrel.

Output

For each testcase print a single positive integer — the minimum number of cups required to be poured into the barrel to achieve the closest temperature to t.

Examples

input

3
30 10 20
41 15 30
18 13 18

output

2
7
1

Note

In the first testcase the temperature after 2 poured cups: 1 hot and 1 cold is exactly 20. So that is the closest we can achieve.

In the second testcase the temperature after 7 poured cups: 4 hot and 3 cold is about 29.857. Pouring more water won‘t get us closer to t than that.

In the third testcase the temperature after 1 poured cup: 1 hot is 18. That‘s exactly equal to t.

题意

拥有无数杯冷水无数杯热水，热水温度为 h ，冷水温度为 c

从热水开始，每次交替 热水-冷水 倒入另一个盆中

盆中水的温度为倒入的水温平均值

问最少倒几次能使得盆中水的温度最接近于 t

解题思路

从热水开始，每次交替倒入盆中

可以发现如果倒的次数为偶数次，那么盆中水温一定为冷热水的平均值 (h+c)/2 ，令这个平均值为 mid

而如果倒的次数为奇数次，那么盆中水温将随着倒的次数的增多，从 h 开始往 mid 靠拢

得到如下图示

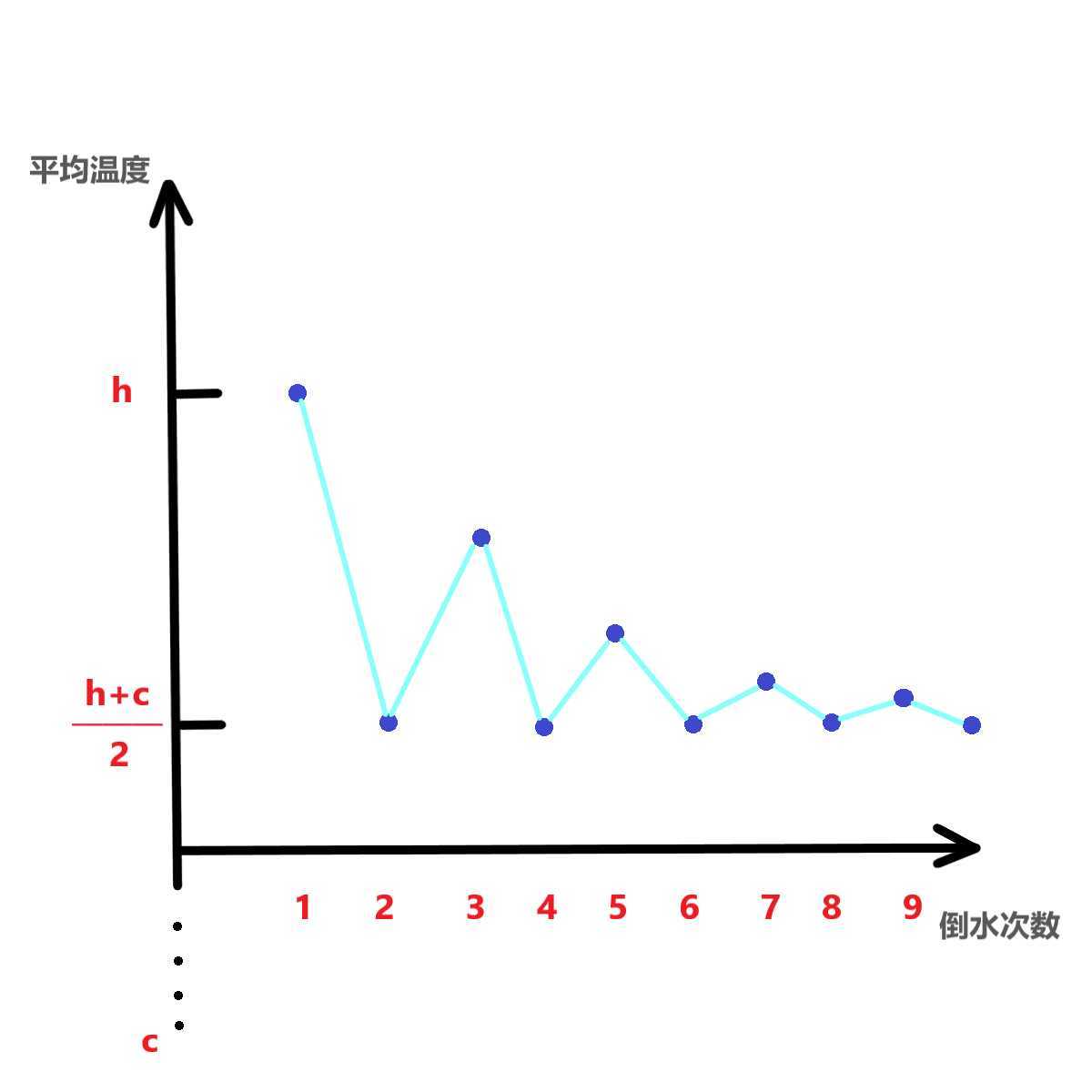
所以首先得出两个特判

如果 t>=h 输出 1

如果 t<=mid 输出 2

剩余的，即 mid<t<h 的部分，首先可以得到他们需要的倒水次数一定是奇数

且如果倒水次数从 1 开始，按照 1 3 5 7 ... 的顺序计算水温

则肯定会有某一次操作 x 使得水温 >= t ，且第 x+2 次操作使得水温 < t

但是从 1 开始每次 +2 枚举，配合上数据组数会导致超时

所以还是要从公式入手

可以得到，如果操作次数为偶数次，则平均水温一定为 mid

但此时答案操作次数为奇数次，令答案为 ans

则操作 ans-1 次时，得到水温总和为 (ans-1)*mid

第 ans 次加入的是热水 h

所以可以得到如下公式

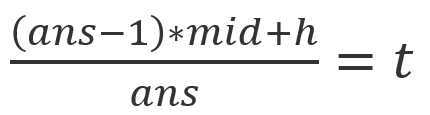
移项得

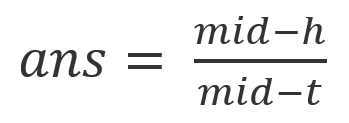
所以可以得到答案的近似操作次数

由于操作次数一定是个整数，所以可以在求出此时的 ans 后，在 ans 周围枚举判断下哪一次操作才是真正的答案

计算误差不会太大，所以在 ±3 范围内查找即可

完整程序

#include<bits/stdc++.h>
using namespace std;

void solve()
{
    double h,c,t,mid;
    cin>>h>>c>>t;
    mid=(h+c)/2.0;
    
    if(h<=t)
    {
        cout<<1<<‘\n‘;
        return;
    }
    if(mid>=t)
    {
        cout<<2<<‘\n‘;
        return;
    }
    
    int d=(mid-h)/(mid-t),ans,i;
    double delta=1e8,tmp;
    
    i=max(1,d-3); //最小值不能小于 1
    if(i%2==0)
        i--; //必须是奇数
    for(;i<=d+3;i+=2)
    {
        tmp=fabs(1.0*((i-1)*mid+h)/i-t); //计算操作i次的水温差值
        if(tmp<delta)
        {
            delta=tmp;
            ans=i;
        }
    }
    
    cout<<ans<<‘\n‘;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int T;cin>>T;
    while(T--)
        solve();
    return 0;
}

Codeforces 1359C - Mixing Water （数学）

原文：https://www.cnblogs.com/stelayuri/p/12985058.html