李宏毅深度学习笔记 https://datawhalechina.github.io/leeml-notes
李宏毅深度学习视频 https://www.bilibili.com/video/BV1JE411g7XF
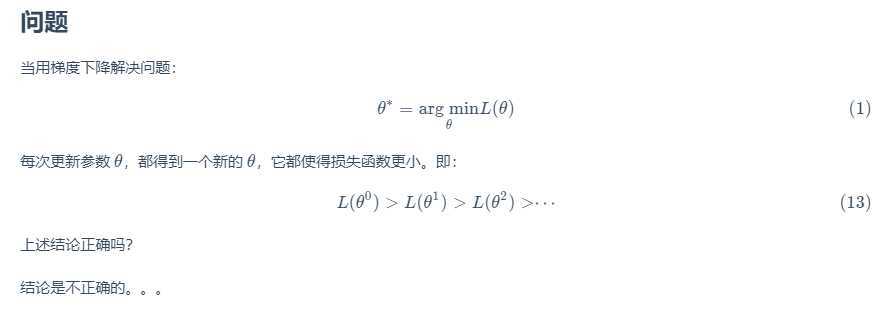
\(\theta_0\)时,在一个小范围圆圈内找到一个损失极小时的\(\theta_1\),再在\(\theta_1\)一个小范围圆圈内找一个\(\theta_2\),不断地去找
如何快速找到圆圈内的极小值?
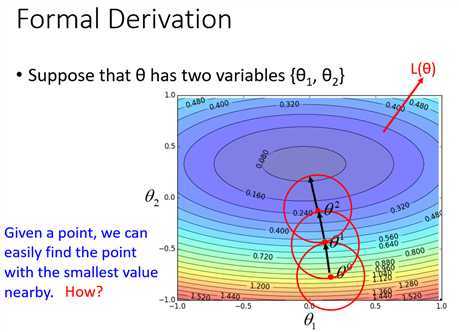
泰勒展开式

\(x\)趋向于\(x_0\)时,2阶和之后的项可以看成\(\Delta x\)的高阶无穷小
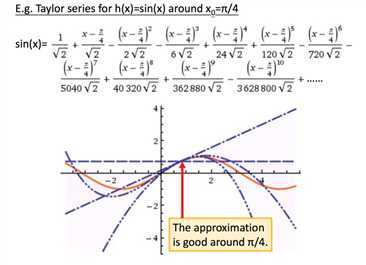
泰勒展开有个条件是\((x-x_0)\)趋向于0,意思是在\(x_0\)的无穷小范围内,曲线无限近似于真实的曲线

多个变量时,则要考虑所有变量的偏微分
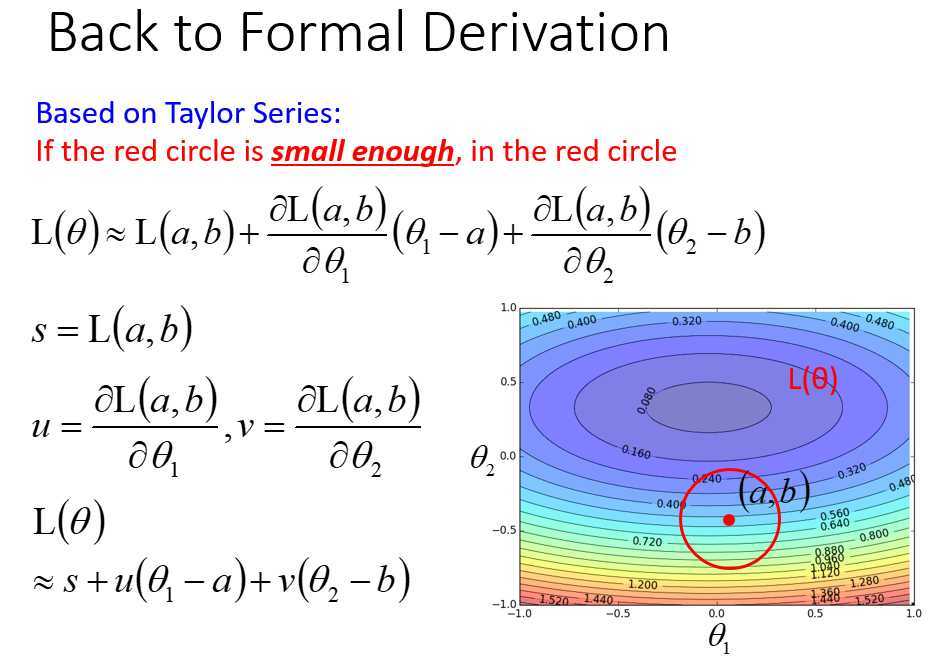
利用泰勒展开式,在点(a,b)泰勒展开,在红色圆圈内找\(L(\theta)\)最小时的\(\theta_1,\theta_2\)
注意\((u,v)\)看成一个向量
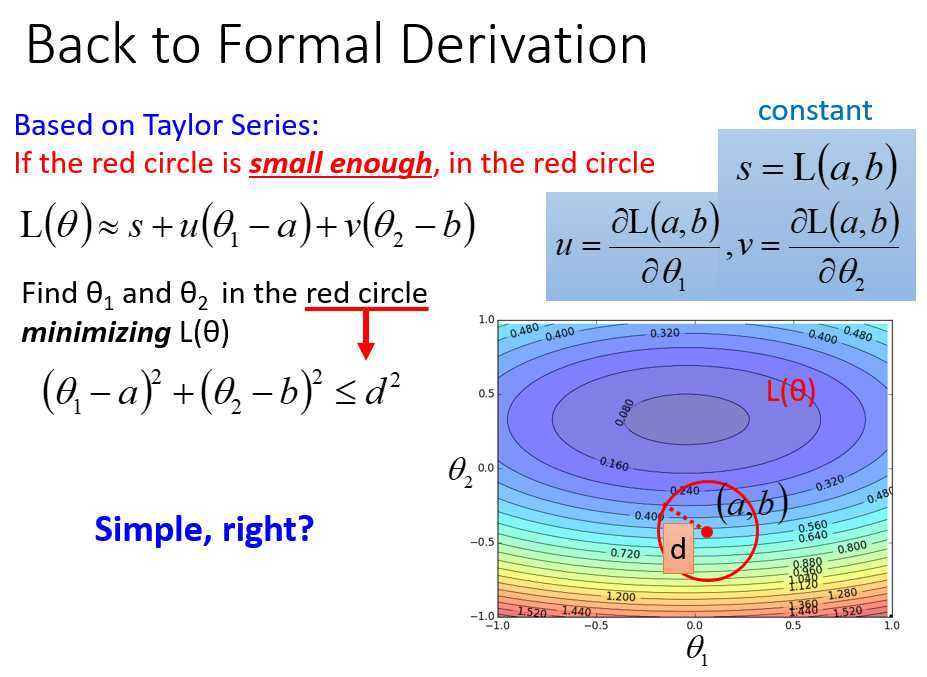
极小化\(L(\theta)\),忽略\(s\),相当于极小化\((\Delta \theta_1,\Delta \theta_2)\)和\((u,v)\)的点积,明显反向时点积最小
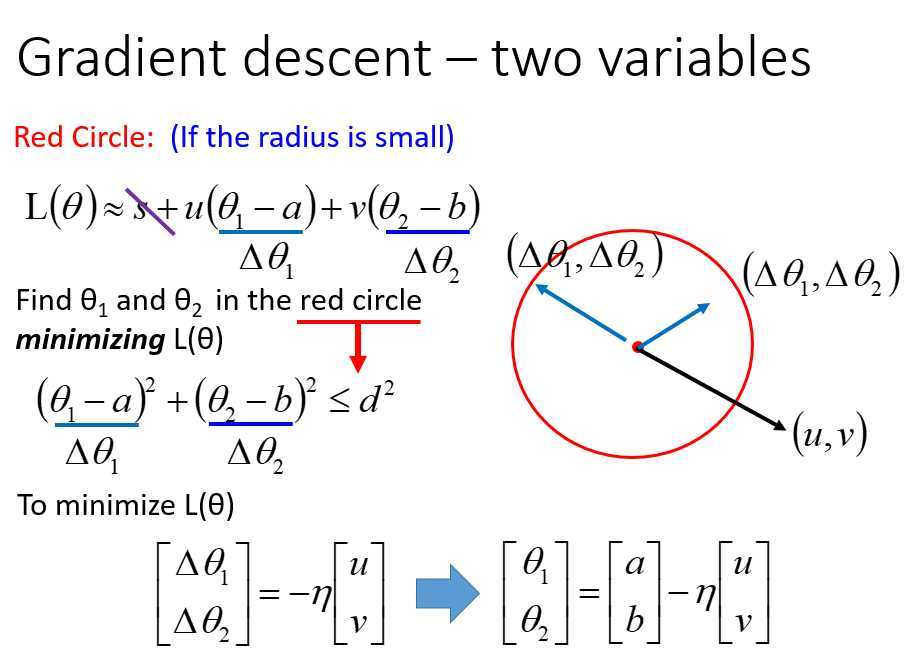
因为有圆圈约束,即\((\Delta \theta_1^2+\Delta \theta_2 ^2) \leq d^2\),要乘以一个\(\eta\)
这里乘以\(\eta\) 的原因是因为,两个向量共线,\(\theta_1,\theta_2\)共用一个\(\eta\)

泰勒展开找极小值迭代参数的公式和梯度下降的迭代公式是一样的
应用泰勒展开最重要的就是,\(x-x_0\)必须足够的小,不然会有较大的误差,即红色圆圈必须足够小
那么\(\eta\) (学习率) 就不能太大,因为红色圆圈的半径和\(\eta\) 成正比
梯度下降就考虑了一次微分,像牛顿法会涉及到二次微分,精度会好,但是运算消耗会变大
梯度下降的限制
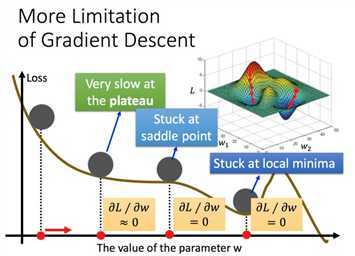
下降过程中,可能会进入局部极小点,鞍点,这些地方微分值都等于0
也可能停在微分小于某个阈值的地方
原文:https://www.cnblogs.com/wry789/p/12989805.html