题目描述

题解

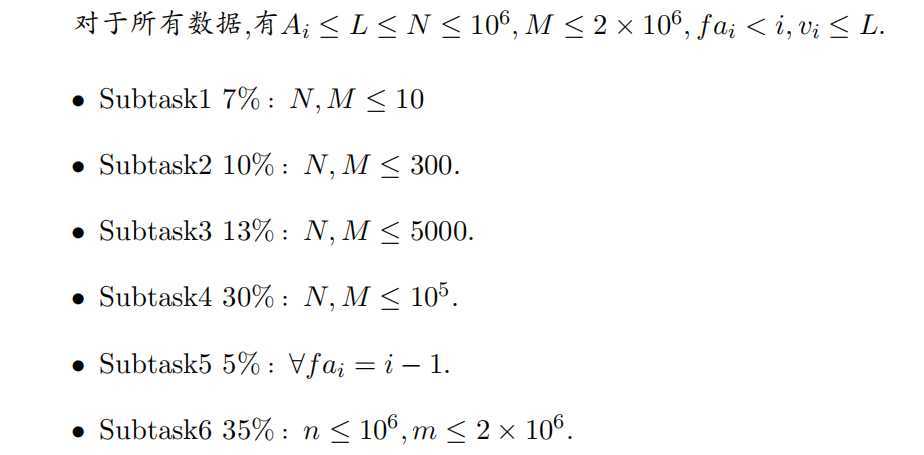
由于修改的标号单调且fa[i]<i，那么一定是从上往下搞♂

对于一次修改求出加/减的序列数，根据当前的x和到根的前缀上x+1~L的和子树内1~x-1的可以算出

到根的dfs算，子树内的可以启发式合并/线段树合并

想想发现可以直接维护dfs序中前缀的答案，子树内的答案减一下即可得到

时间复杂度O(n)

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 1000000007
#define ll long long
#define file
using namespace std;

int a[1000002][2],ls[1000002],A[1000002],v[3000002],fa[1000002],n,m,M,L,I,i,j,k,l,len,tot,ntt;
ll f[1000002],F[1000002],s1[1000002],s2[1000002],g[1000002],G[1000002],ans,Ans;

void Read(int &x) {x=0;char ch=getchar(); while (ch<‘0‘ || ch>‘9‘) ch=getchar(); while (ch>=‘0‘ && ch<=‘9‘) x=x*10+(ch-‘0‘),ch=getchar();}
void swap(int &x,int &y) {int z=x;x=y;y=z;}
void New(int x,int y) {++len;a[len][0]=y;a[len][1]=ls[x];ls[x]=len;}
void dfs(int t)
{
	int i;
	ll s;
	
	s1[t]=G[A[t]-1],s2[t]=G[v[ntt+t]-1];
	f[t]=(t==1)?1:g[A[t]+1];F[t]=(t==1)?1:g[v[ntt+t]+1];
	if (A[t]==1) Ans+=f[t];
	
	s=g[A[t]];
	g[A[t]]=(g[A[t]]+f[t])%mod;
	for (i=ls[t]; i; i=a[i][1]) dfs(a[i][0]);
	g[A[t]]=s;
	
	s1[t]=(A[t]==1)?1:(G[A[t]-1]-s1[t])%mod,s2[t]=(v[ntt+t]==1)?1:(G[v[ntt+t]-1]-s2[t])%mod;
	G[v[ntt+t]]=(G[v[ntt+t]]+s2[t])%mod;
}

int main()
{
	freopen("scholar.in","r",stdin);
	#ifdef file
	freopen("scholar.out","w",stdout);
	#endif
	
	Read(n);Read(m);Read(L);
	fo(i,2,n) Read(fa[i]),New(fa[i],i);
	fo(i,1,n) Read(A[i]);
	fo(i,1,m) Read(v[i]),swap(v[i],A[(i-1)%n+1]);
	M=m;
	while (m%n) ++m,v[m]=A[(m-1)%n+1];
	
	fd(i,m,1)
	{
		if (!(i%n) && i+n<=m) memset(G,0,sizeof(G));
		if (!(i%n)) Ans=0,tot=i/n-1,ntt=n*tot,dfs(1),Ans%=mod;
		if (i<=M) ans=(ans+Ans*i)%mod;
		
		I=(i-1)%n+1;
		if (i<=M)
		Ans=(Ans-s1[I]*f[I]+s2[I]*F[I])%mod;
		A[I]=v[i];
	}
	printf("%lld\n",(ans+mod)%mod);
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}

6655. 【2020.05.27省选模拟】三国学者

原文：https://www.cnblogs.com/gmh77/p/12989665.html