在数学的分支图论中,图(Graph)用于表示物件与物件之间的关系,是图论的基本研究对象。一张图由一些小圆点(称为顶点或结点)和连结这些圆点的直线或曲线(称为边)组成

有向图&无向图:图中的边是否有方向。
入度与出度(有向图的顶点),入度:以当前顶点为终点的边的数量;出度:以当前顶点为起点的边的数量
路径:从u到v的一条路径是指一个序列v0,e1,v1,e2,v2,...ek,vk,其中ei的顶点为vi及vi - 1,k称作路径的长度。如果它的起止顶点相同,该路径是“闭”的,反之,则称为“开”的。一条路径称为一简单路径(simple path),如果路径中除起始与终止顶点可以重合外,所有顶点两两不等。边的序列
环:起点与终点重合的路径;自环:一条边的两顶点相同
DAG:有向无环图
图的存储
邻接矩阵:使用一个二维数组g(i,j)表示图中各个顶点的联系。若边存在权值,则g(i,j)记录i -> j的相应权值;否则赋值为1,表示i - > j,存在边。
邻接表:链式前向星(速度较vector实现更快)
const int kN = 1010;
struct node{
int e,ne,w;//终点,与当前边同起点的下一条边的索引,权值
}g[kN];
int idx,n,h[kN];//idx 边的索引 h数组,存储各个头结点中 -- 索引最大的边(数组模拟链表,头插法)
void add(int a,int b,int c){//a - b,权值w
g[idx].e = b;
g[idx].ne = h[a];
g[idx].w = c;
h[a] = idx++;//更新当前起始节点中边的最大索引
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(0);
int a,b,w;
memset(h, -1, sizeof h);
cin >> n;
for(int i = 0; i < n; i++){
cin >> a >> b >> w;
add(a,b,w);//有向图
//add(b,a,w);
}
for(int i = 0; i < n; i++){//遍历图
for(int j = h[i]; j != -1; j = g[j].ne){//遍历以i为起点所有边
cout << i << "->" << g[j].e << ‘ ‘ << g[j].w << endl;
}
}
return 0;
}
十字链表
DFS&BFS
//dfs求最短路,遍历所有路径,维护min
int g[kN][kN],ans = 0x3f3f3f3f;
bool vis[kN][kN];
void dfs(int s,int dist){//当前节点编号,所走过的路径
if(dist > ans) return;
if(s == n){
if(ans > dist) ans = dist;
return;
}
for(int i = 1; i <= n; i++){
if(g[s][i] != -1 && !vis[s][i]){//s,i间未到达的边
vis[s][i] = true;
dfs(i, dist + g[s][i]);
vis[s][i] = false;
}
}
}
//bfs,起始节点入队,按层搜索相邻节点 -- end
#define first x//节点编号
#define second dist//到此节点的最短路
void vfs(){
pair<int,int> cur,top;
queue<pair<int,int> > q;
q.push(make_pair(sx,sy));
vis[sx] = true;
while(!q.empty()){
top = q.front();
q.pop();
if(top.x == end){
cout << top.dist << endl;
return;
}
cur.dist = top.dist + 1;
for(int i = 1; i <= n; i++){
if(g[top.x][i] != -1 && !vis[i]){
cur.x = i;
q.push(cur);
vis[i] = true;
}
}
}
}
最短路:
a->b节点的最短路:1. 直接到达(相邻);2.借助其他顶点中转到达;
边权为正的图,任意两顶点的最短路,不会经过重复的节点 or 边,路径中的节点数不会超过n,边不会超过n -1条。
松弛:通过方法2,使路径变短的操作
单源最短路:定点到其它顶点的最短路
Dijkstra算法(不能处理负权边 -- 有负环,贪心不成立 ):先选择一个距起始点最近的顶点加标记,通过这两点的最短路径去更新起点到达其它顶点的最短路(dist数组)。之后不断的选择当前未标记的距起点路径最短的点去松弛其他的点.--贪心:每次使用当前最短路径的点去松弛与它相邻的点。
const int inf = 0x3f3f3f3f;
int n,g[kN][kN],dist[kN];//dist数组存储定点到其它各点的最短路
bool vis[kN];
void dijkstra(int s,int e){
memset(dist,0,sizeof dist);
memset(vis,0,sizeof vis);
dist[s] = 1;//s -> s 安全系数为1
vis[s] = true;
int t;
for(int i=1;i<n;i++){
t = -1;
for(遍历以i为起始节点的所有边,另一个结点j){
//找到当前未访问过的距定点路径最短的点
//在未到达的点上 若有更小的dist 修改t
if(!vis[j] && (t == -1 || dist[t] > dist[j])) t = j;
}
vis[t] = true;
//通过t点松弛它的相邻顶点
for(int j=1;j<=n;j++){
if(dist[j] < (dist[t]+g[t][j])) dist[j] = dist[t]+g[t][j];
}
}
}
void floyd(){
for(int k=0;k<n;k++){//借助所有点中转
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
g[i][j] = min(g[i][j],g[i][k] + g[k][j]);
}
}
}
}
int u[kN],v[kN],W[kN],dist[kN];//U -> v 权值为w
for(int k = 1; k <= n - 1; k++){
for(int i = 1; i <= m; i++){//遍历m条边,可否通过u->v这条边缩短dist[v[i]] -- 松弛
if(dist[v[i]] > dist[u[i]] + w[i]) dist[v[i]] = dist[u[i]] + w[i];
}
}
struct node{
int e,ne,w;
}edge[kN];
int head[kN],idx,n,m,t;
//bfs判负环,入队次数大于n,复杂度有点高...
bool spfa(){
queue<int> q;
q.push(s);
vis[s] = true;//入队加标记,出队取消标记
while(!q.empty()){
int top = q.front();
q.pop();
vis(top) = false;
for(int v = head[top]; v != -1; v= edge[v].ne){//遍历以top为起点的所有边
if(relax(u,v) && !vis[v]){
q.push(v);
vis[v] = true;
}
}
}
}
//SLF优化:优先队列优化的SPFA,权值高的元素排在队首 -- 有负权边:复杂度会卡到2的指数级
//dfs版 判断(多次入队)及之后的退出上更快
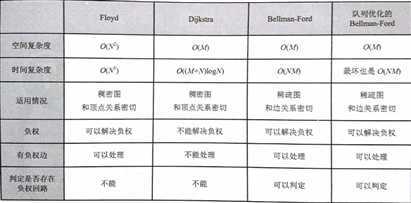
各算法对比 -- 《啊哈 !算法》
最小生成树: 边权和最小的生成树O(mlogm)
int x,f[kN];
struct edge{
int form,to,value;
}
int kruskal(edge *edges,int m){//边集 大小
sort(edges,edges + m,cmp);//按边权升序排列
int r = 0;//权
for(int i = 0; i < m; i++){
if(find(deges[i].from) == find(edges[i].to)) continue;//成环,在同一连通块中
r += edges[i].value;//边权加入权值和
unionn(edges[i].from,edges[i].to);//合并连通块
}
return r;
}
prim
int edges[N][N],dist[N];
bool vis[N];
int prim(int n){
vis[1] = true;//任一节点开始
for(int i = 2; i <= n; i++) dist[i] = edges[1][i];
int ret = 0;
for(int i = 2; i <= n; i++){
int x = 1;
for(int j = 1; j <= n; j++){//寻找最小权值
if(!vis[j] && dist[j] > dist[x]) x = j;
}
ret += dist[x];
vis[x] = true;
for(int j = 1; j <= n; j++){//更新dist x -> 其他节点
if(!vis[j]) dist[j] = max(dist[j],edges[x][j]);
}
}
return ret;
}
原文:https://www.cnblogs.com/honey-cat/p/12990057.html