给定一个长度为N的数列A,以及M条指令,每条指令可能是以下两种之一:
1、“C l r d”,表示把 A[l],A[l+1],…,A[r] 都加上 d。
2、“Q l r”,表示询问 数列中第 l~r 个数的和。
对于每个询问,输出一个整数表示答案。
第一行两个整数N,M。
第二行N个整数A[i]。
接下来M行表示M条指令,每条指令的格式如题目描述所示。
对于每个询问,输出一个整数表示答案。
每个答案占一行。
1≤N,M≤1051≤N,M≤105,
|d|≤10000|d|≤10000,
|A[i]|≤1000000000
差分后我们可以做到logn的进行对一个值的询问,但是这里问的是个范围,如果m次询问l-r的范围的话,复杂度是m*n*logn,显然是不可的先看一下l-r的值是什么:
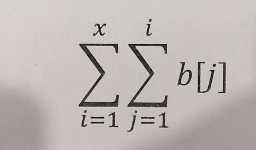
等价于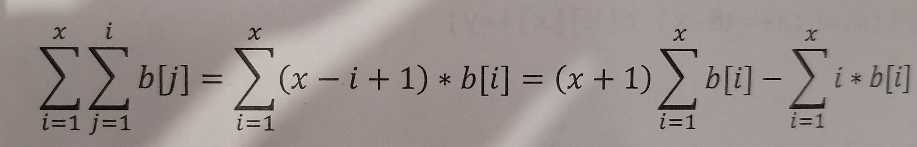
拆成这样的形式后我们只需要见两个数组,一个是a[i]差分,另一个是i*a[i]的差分
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int SIZE=100010; int a[SIZE],n,m; long long c[2][SIZE],sum[SIZE]; long long ask(int k,int x) { long long ans=0; for(;x;x-=x&-x) ans+=c[k][x]; return ans; } void add(int k,int x,int y) { for(;x<=n;x+=x&-x) c[k][x]+=y; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); sum[i]=sum[i-1]+a[i]; } while(m--) { char op[2]; int l,r,d; scanf("%s%d%d",op,&l,&r); if(op[0]==‘C‘) { scanf("%d",&d); add(0,l,d); add(0,r+1,-d); add(1,l,l*d); add(1,r+1,-(r+1)*d); } else{ long long ans=sum[r]+(r+1)*ask(0,r)-ask(1,r); ans-=sum[l-1]+l*ask(0,l-1)-ask(1,l-1); printf("%lld\n",ans); } } }
其实这题线段树显然更容易理解,今天会更出线段树
原文:https://www.cnblogs.com/ilikeeatfish/p/12990642.html