思维导图
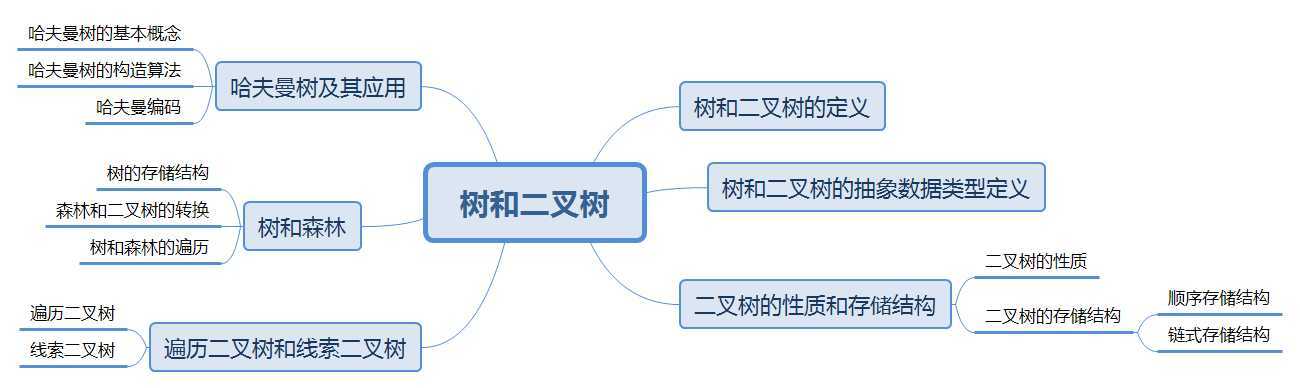
重要知识点总结
术语:
二叉树具有下列重要特性:
二叉树的二叉链表存储表示:
typedf struct BiTNode { int data; //结点数据域 struct BiTNode *lchild ,*rchild; //左右孩子指针 }BiTNode,*BiTree;
中序遍历的递归算法:
void InOrder(BiTree T) { if(T == NULL) return; else { InOrder(T->lchild); //中序遍历左子树 cout<<T->data;//访问根节点 InOrder(T->rchild); } }
先序遍历的顺序建立二叉链表:
void creat(BiTree &T) {//根据读入的先序字符序列建立二叉树 char ch; cin>>ch; if(ch == ‘#‘) T = NULL;//递归结束,建空树 else { T = new BiTNode; T->data = ch;//生成子树根结点 creat(T->lchild);//递归创建左子树 creat(T->rchild); } }
统计二叉树中结点个数:
int CountLeaves(BiTree T)//统计T指向的二叉树的叶子结点的个数 { if(T == NULL) return 0; else if(T->lchild == NULL && T->rchild == NULL) return 1; return CountLeaves(T->lchild)+CountLeaves(T->rchild)+1;//注意加一 }
哈夫曼树:给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。
构造过程
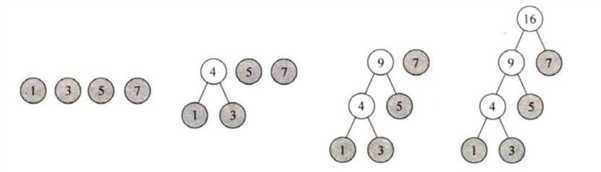
void CreateHuffmanTree(HuffmanTree &T ,int n) { if(n<=1)return ; m = 2*n-1; HT = new HTNode[m+1];//动态分配 //初始化 for(i = 1;i<=m;i++) { HT[i].parent = 0 ; HT[i].lchild = 0 ; HT[i].rchild = 0 ; } for(i=l;i<=n;++i}//输人前n个单元中叶子结点的权值 cin>>HT[i] .weight; for (i=n+l; i<=m; ++i) {//通过n-1次的选择、删除、合并来创建哈夫曼树 Select (HT, i-1, s1, s2); HT[i] .lchild=s1; HT [i]. rchild=s2; / /sl, s2分别作为i的左右孩子 HT[i] .weight = HT[s1] .weight+HT[s2] .weight; }
}
树的存储结构:双亲表示法、孩子表示法和孩子兄弟表示法,孩子兄弟表示法是常用的表示法,任意一棵树都能通过孩子兄弟表示法转换为二叉树进行存储。
错题分析
1.
typedef struct { int child; CNode *next; }CNode;
"*next"处出错,因为CNode尚未声明。应在typedef struct后面加上CNode!
2.

合法,属于堆空间申请(分配与回收人工操作)。
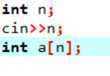
C中ok,但在C++中不安全,属于栈空间申请。
总结
第五章又开始了一个新的篇章,但是由于前段时间没有对之前的知识进行深层的理解,导致刚开始这部分的时候变得力不从心。从来不应该"捡芝麻丢西瓜",接下来的时间将进行全面的一个查漏补缺(重点在实现方法)。
原文:https://www.cnblogs.com/wftblog/p/13021142.html