一、树
|
线性结构 |
树形结构 |
|
第一个数据元素(无前驱) |
根结点(无前驱) |
|
最后一个数据元素(无后继) |
多个叶子结点(无后继) |
|
其他数据元素(一个前驱+一个后继) |
其他数据元素(一个前驱+多个后继) |
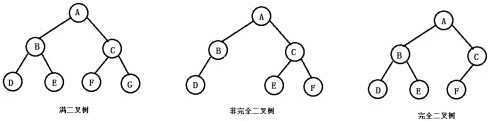
二、二叉树
|
类别 |
辨析 |
|
满二叉树 |
每一层都充满了结点,达到最大结点数 |
|
完全二叉树 |
除最后一层外,每一层都是满的,且最后一层结点从左向右出现 |
|
非完全二叉树 |
除最后一层外,每一层都是满的,最后一层结点不按从左向右出现 |
(一) 二叉树的性质
性质1:第i层的结点个数至多2^(i-1) 【若m叉树,则为m^(i-1)】
性质2:设深度为k,结点个数至多(2^k)-1
性质3:若叶子数为n0,度为2的结点数为n2,则n0=n2+1
n=n0+n1+n2 ……①
n=B(分支总数)+1 = n1+2n2+1 ……② // B = n0*0+n1*1+n2*2+……+nk*k
n0=n2+1 ……③
性质4:n个结点的完全二叉树深度:(int)log2(n) + 1
性质5:完全二叉树从上至下,从左至右编号,对于编号为i的结点,左孩子编号必为2i,右孩子编号必为2i+1,双亲编号必为i/2(向下取整)
|
|
结点 |
叶子 |
分支 |
层数 |
深度 |
|
性质1 |
? |
|
|
? |
|
|
性质2 |
? |
|
|
|
? |
|
性质3 |
? |
? |
|
|
|
|
性质3 推导公式 |
? |
? |
? |
|
|
|
性质4 |
? |
|
|
|
? |
|
性质5 |
? |
|
|
|
|
(二) 二叉树/树的存储
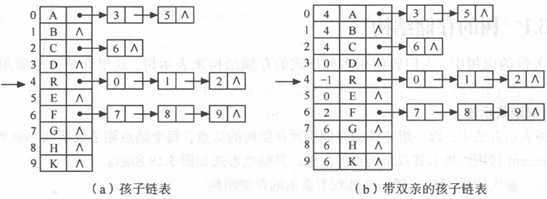
1、 链式存储

1 #define Maxsize 100 2 typedef struct CNode 3 {//孩子结点 4 int child;//孩子结点下标 5 struct CNode *nextchild; 6 }CNode; 7 8 typedef struct 9 {//每个结点 10 int parent;//父结点下标 11 char data; 12 CNode *firstchild;//孩子结点链表CNode头指针 13 }PNode; 14 15 typedef struct 16 {//树 17 PNode nodes[Maxsize]; 18 int root;//根结点下标 19 int n;//树的结点数 20 }Tree; 21 22 /* 23 typedef struct 24 {//树 25 PNode *nodes;//在初始化时使用new来申请空间 26 int root; 27 }Tree; 28 Tree t; 29 t.nodes = new PNode[Maxsize]; 30 */
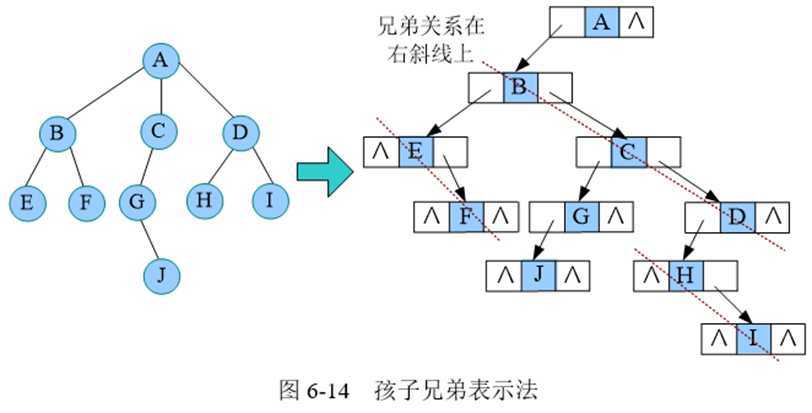

1 typedef struct CSNode 2 { 3 char data; //ElemType data; 4 struct CSNode *firstchild, *nextchild, *nextsibling; 5 }CSNode, *CSTree;
2、 顺序存储

1 #define Maxsize 100 2 typedef struct 3 { 4 char data; 5 int lch; 6 int rch; 7 }Node; 8 9 typedef struct 10 { 11 Node data[Maxsize]; 12 int root;//根结点编号 13 }Tree;
|
存储方式 |
结点下标 |
Data |
Child下标 |
Child指针 |
Parent下标 |
|
|
链式存储 |
孩子链表 |
? |
? |
? (此时以结构体形式存在,非下标值) |
? |
|
|
带双亲的孩子链表 |
? |
|||||
|
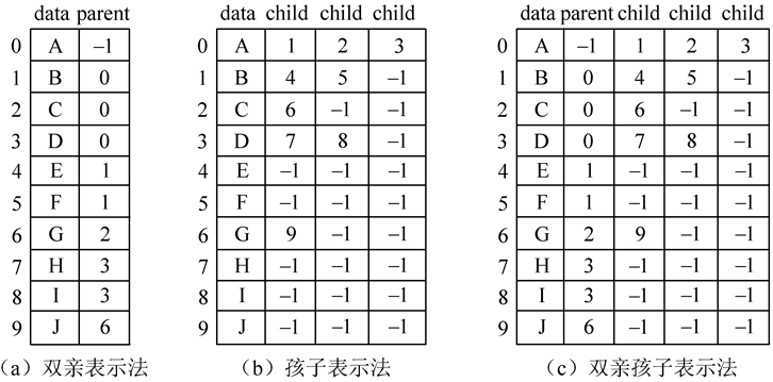
顺序存储 |
双亲表示法 |
? |
? |
? |
||
|
孩子表示法 |
? |
|||||
|
双亲孩子表示法 |
? |
|||||
(三) 二叉树的遍历
1、 先序遍历(根、左子树、右子树)注:递归思想,一定要等左子树遍历完,才能遍历右子树

1 void preorder(Btree T) 2 { 3 if(T)//if(T!=NULL) 4 { 5 cout<<T->data; 6 preorder(T->lchild); 7 preorder(T->rchild); 8 } 9 }
2、 中序遍历(左子树、根、右子树)

1 void inorder(Btree T) 2 { 3 if(T) 4 { 5 inorder(T->lchild); 6 cout<<T->data; 7 inorder(T->rchild); 8 } 9 }
3、 后序遍历(左子树、右子树、根)

1 void posorder(Btree T) 2 { 3 if(T) 4 { 5 posorder(T->lchild); 6 posorder(T->rchild); 7 cout<<T->data; 8 } 9 }
4、 层次遍历(从上到下,从左到右)

1 bool Leveltraverse(Btree T) 2 { 3 Btree p; 4 if(!T) 5 return false; 6 queue<Btree>Q; //创建一个普通队列(先进先出),里面存放指针类型 7 Q.push(T); //根指针入队 8 while(!Q.empty()) //如果队列不空 9 { 10 p=Q.front();//取出队头元素作为当前扩展结点livenode 11 Q.pop(); //队头元素出队 12 cout<<p->data<<" "; 13 if(p->lchild) 14 Q.push(p->lchild); //左孩子指针入队 15 if(p->rchild) 16 Q.push(p->rchild); //右孩子指针入队 17 } 18 return true; 19 }
三、哈夫曼树
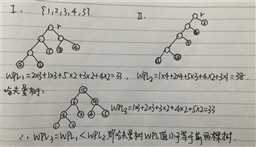
思想:自底向上,让权值大的叶子离根近
方法:每次从树中选取没有双亲且权值最小的两棵树作为左、右子树,构造一棵新树,并将其插入原树,新树的根结点的权值为其左右孩子结点权值之和。
结论:1、哈夫曼树WPL值一定小于等于其他树
2、哈夫曼树一定是最优二叉树,最优二叉树不一定是哈夫曼树
原文:https://www.cnblogs.com/originaldoll/p/12976612.html