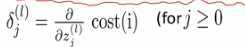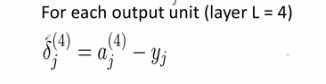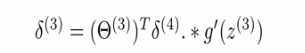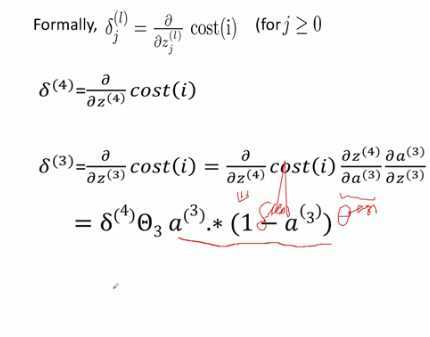神经网络概述与发展
概述
- 最初:算法企图模仿人脑
- 在上世纪80s和90s被广泛的应用;但在90s后期不再受关注,因为svm的兴起,人们觉得研究神经网络没前途
- 最近的复兴,随着深度学习兴起,提高了许多应用的最高水平,再度兴起
应用案例:
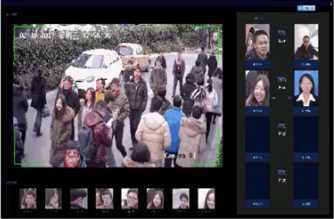
1.人脸识别
2.智能翻译
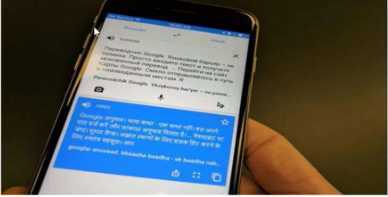
这些技术的背后都是基于神经网络,暗示着神经网络的复兴。
发展
1.生物学上发现人脑是由大量神经元构成的。

2.每个神经元都是和其他神经元连接,神经元与神经元之间有信号传输
3.生物学上的神经元认识
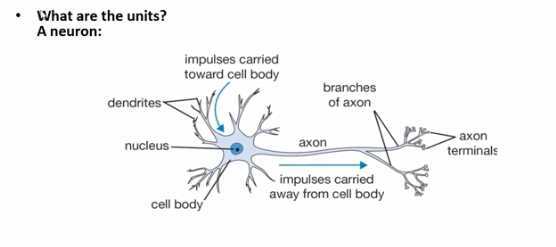
- 每个神经元和其他神经元连接,并相互传播信号
- 信号通过树突传入神经元
- 信号通过轴突传出神经元
- 神经网络创始人

1943年,心理学家McCulloch和逻辑学家Pitts参考了生物神经元的结构,发表了抽象的神经元模型.MP
神经网络基本概念
神经元模型
神经元模型是一个包含输入、输出与计算功能的模型。
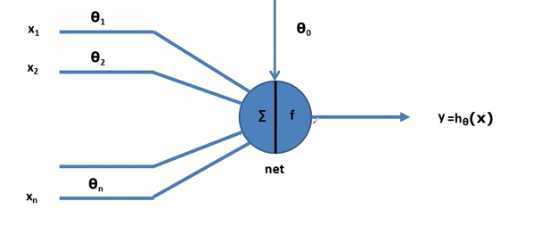
- x1,x2,x3,...,xn输入信号
- θ1,θ2,,....θn是权值,代表神经元与神经元之间连接的强弱
- 神经元会对输入信号做处理,做的处理是加和处理,其实就是线性变换
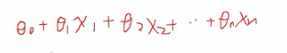
- 对做了线性变换的值,再经过一个函数,变换一下,类似逻辑回归:
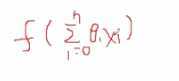
激活函数
输入可以类比为神经元的树突,而输出可以类比为神经的轴突。计算则可以类比为细胞核。f称为**激活函数**(activation function)
- 对于一个神经元来说其具有两个状态,激活状态和非激活状态。一个神经元是否激活激活函数有关,因为是两个状态,所以类似于分类,激活函数有许多种
:
阈值激活函数
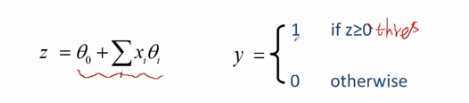
- z是经过了线性变换的结果
- 如果z>=0,那么神经元输出1,该神经元处于激活状态,如果z<0,那么神经元输出0,该神经元处与非激活状态
符号激活函数
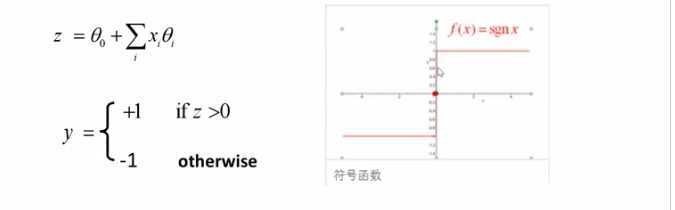
sigmoid激活函数
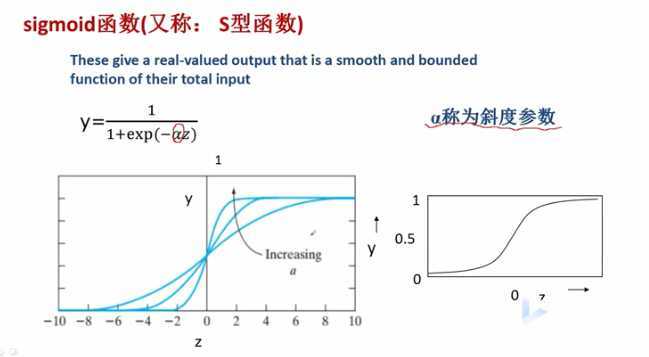
sigmoid函数是一个连续的,而且s型的函数,α值称为斜度参数,α值越大,曲线越陡峭,α越小越平
sigmoid函数作为激活函数的优点:
- 非线性
- 单调性
- 无限次可微(最大优点)
- 当a很大时近似阈值函数
- 当a很小时近似线性函数
- 它能够将输入的连续实值压缩到[0,1]之间;特别的,如果是非常大的负数,那么输出就接近0;如果是非常大的正数,输出就接近1.
- 一度是被广泛使用的激活函数,能被解释为-一个神经元的"激活率"
sigmoid函数的缺点:
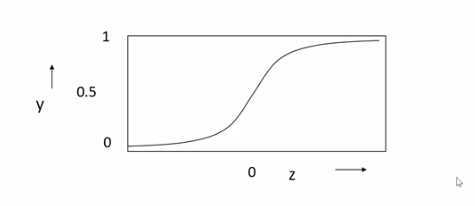
- sigmoid函数在一些位置非常平,进而导数接近于0,梯度下降训练时候我们更新网络参数的时候,参数得不到更新
- sigmoid是非零均值的,它的中心不是0,而是0.5,梯度更新时候会造成震荡
tanh双曲正切函数
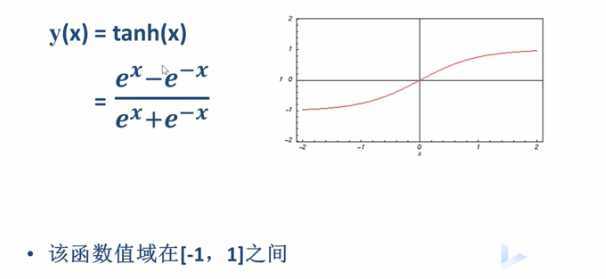
其以0为中心的函数
双曲正切与sigmoid函数的关系:

其一部分梯度为0,的问题依旧存在
校验线性神经元,ReLU

- 准绝对值函数,当值大于0时候,保持本身,否则则为0
- log(1+e^z)函数是一种软的Relu函数
输入层、输出层
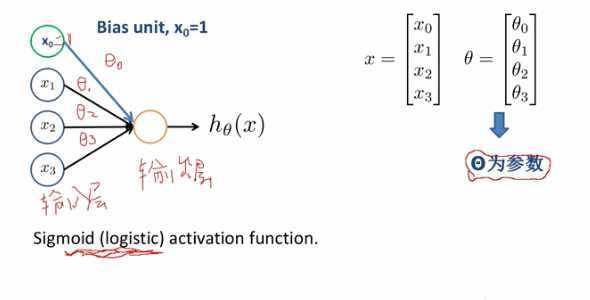
- x0,x1,...,xn叫做输入层
- θ0,θ1,...,θn叫做连接权值,是网络通过学习确定的参数
- 对输入层处理得到输出叫做输出层
简单的神经元就包括输入层和输出层两层
使用神经元来实现简单的运算
神经元实现逻辑与运算
假设我们要用单个神经元,学习到与运算,这里给出权值(实际要学习):
1.与运算就是只有输入两者都是1时候,才输出1,其他情况都输出0
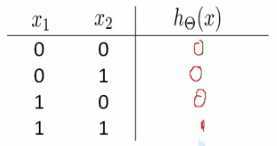
- 假设给定权值,情况下,神经元所进行的运算是:
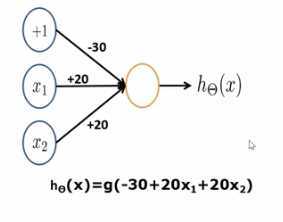
- 参数的表示方法是
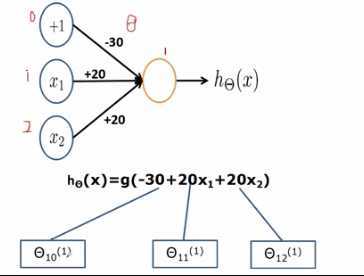
- sigmoid函数
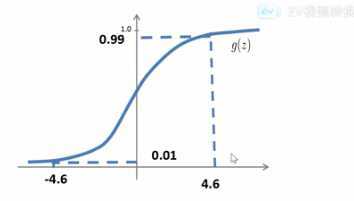
- x=+-4.6时候,y对应0.1和0.99
- 依次代入得到结果,符合与运算
神经元实现逻辑或运算
在给定权值的情况下,观察是否符合或运算:
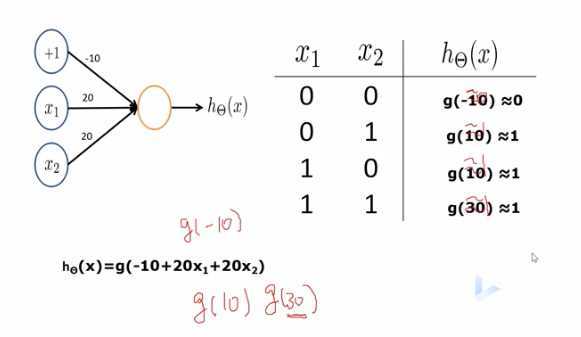
神经元实现逻辑非运算
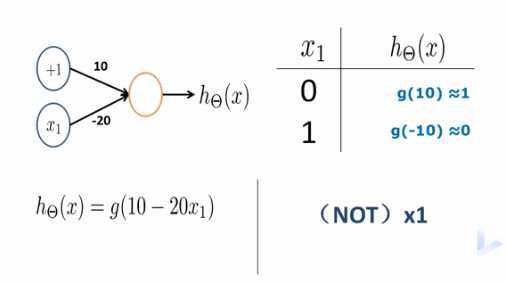
神经元实现异或运算或者异或非运算
- 什么是异或运算,a和b不一样的情况下结果为1,否则为0
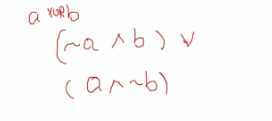
- 什么是异或非运算?,a和b结果一样时候为1,否则为0
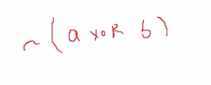
- 这两类点画在平面上
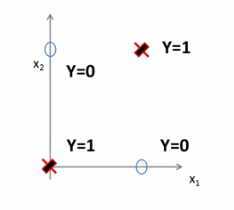
-
要划分这两类点,我们没法找到这样的超平面,将两类点划分开,要解决这两类点划分,没法通过一个神经元划分开,所以没法用一个神经元完成异或或者异或非问题
-
多个神经元完成异或或者异或非运算
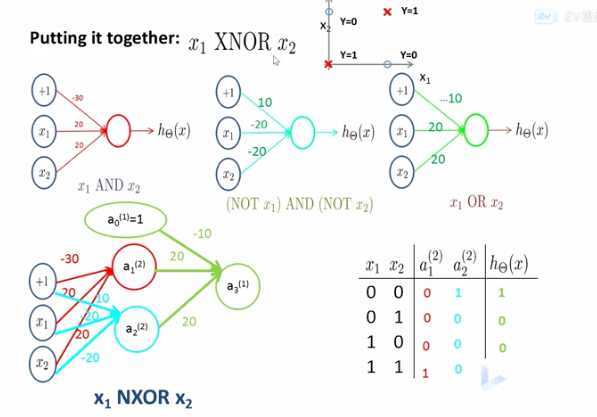
神经网络的表示
之前看到用单个神经元可以组成一个相对复杂的神经网络,来解决复杂的问题,比如异或或者异或非问题。可以学到非线性的决策边界,这样的网络叫做
多层感知积。
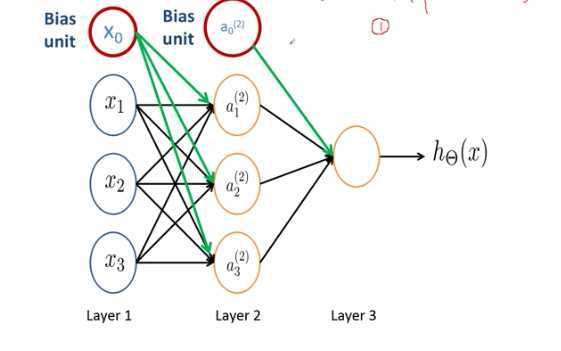
- 每个神经元都和它上一层的所有神经元有连接
- 这样的网络成为全连接的网络
- 同一层的神经元之间没有连接
- 信号从输入层开始逐层的从前往后进行传播,后一层的神经元没有往会的反馈连接
- 这样的网络叫做前馈网络
- 对于单个神经元时候,神经元在接受输入的时候是有偏差项的,也就是比如x0,这样的偏差项的值是恒等于1的

- 对于每个神经元ai(j)表示第j层第i个单元的激励值,也就是激励函数的输出值
- 每一层的神经元和它下一层的神经元都是有连接的,连接权值代表着连接的强度,这么多的权值,可以用权值矩阵来记录权值θ(j),代表从第j层到第j+1层的权值矩阵
- 激励值的计算,代入线性变化后再经过激励函数得到最终的输出
- 关于θ值的意义


同理可以计算其他的激励值;
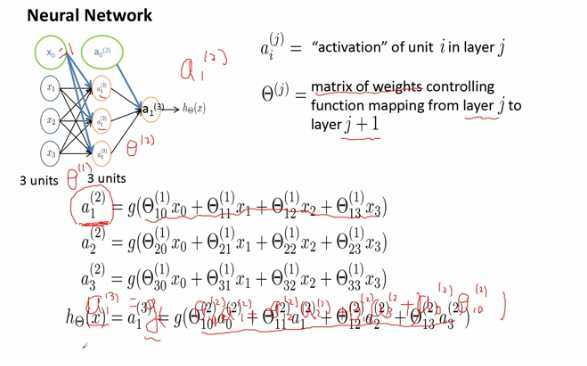
如果将参数放到矩阵θ中去,如果j层有Sj个神经元(不包含偏差项),j+1层有Sj+1个神经元。权值矩阵维度为
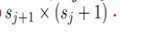
为了简洁可以用矩阵或者向量的形式来表示以上的公式
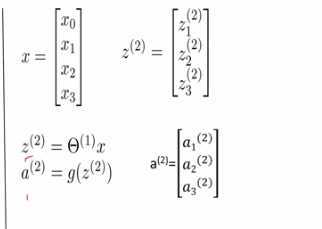
- z都是对输入进行线性变换的结果
- a是由激活函数变换之后得到的结果
- 增加偏差项,计算下一层的值
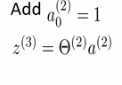
4.再次对输出值做变换
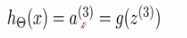
- 隐层在这个过程中学到了什么?
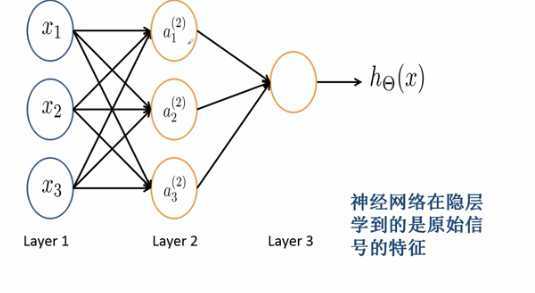
如果将输入层去掉仅仅保留隐层部分,我们将之前网络算出来的输入传递给隐层,作为输入,来计算得到输出。
网络整体得到的输出和之前是一样的,所以说隐层学到来原始信号的特征,隐层取到了特征提取的的作用。对于多层感知机网络
隐藏层最多一到两个隐层,多了会训练不出来。
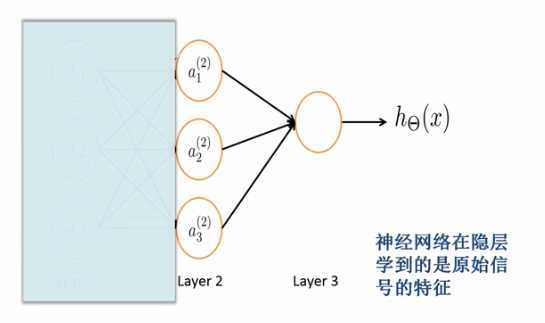
节点的功能
- 在输入层的节点
- 在隐层的节点
- 计算加权和
- 根据激活函数对加权和做变换
- 将和传递给下一层
- 在输出层的节点
1.训练多层神经网络就意味着学习层之间的连接权值
2.理论上包含一个隐层的前馈神经网络,可以建模任意有界的连续函数
感知机的表示能力
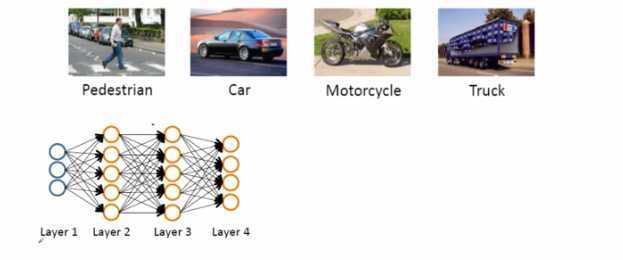
- 神经网络可以做多分类的问题
- 输入层接受输入信号
- 比如将输入信号图片划分成四位,输入应该是图片(300*400),共需要120000个神经元来作为输入层
- 这样的话需要好多个神经元,为了使得不需要这么多神经元,一般输入的都是提取的特征
- 将提取200个特征,作为输入,输入给输入层
- 隐层神经元根据经验确定
- 输出层按照类数,第一个神经元代表是不是汽车,第n个神经元是不是行人....
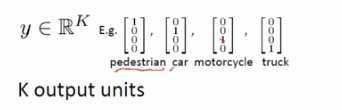
k个输出单元代表分成k类
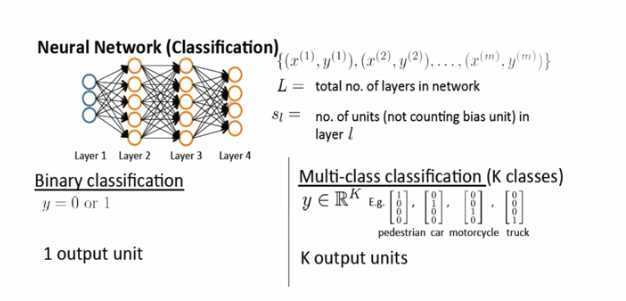
神经网络的数学基础
神经网络算法的流程
同一般的机器学习算法:
- 先定义loss function,衡量模型输出和期望输出之间的差异
- 采用梯度下降算法找到使得loss function取得极小值的参数θ*
- 梯度下降算法需要计算偏导数
- 误差反向传播(BP)算法就是计算偏导数用的
- BP算法的核心是求导链式法则
神经网络的损失函数
一个神经元其实就是一个逻辑回归,那么我们对逻辑回归的损失函数与神经网络的损失函数进行对比:

- 一个神经网络有k个输出,我们用hθ(i)代表第i个输出
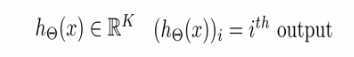
- 神经网络的损失函数,类似于logistics回归的损失函数,对于神经网络来说要将每一个神经元的交叉熵损失都计算出来

- 关于正则化项

梯度概念
- 对于该目标函数:
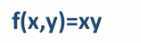
- 分别对x和y求偏导数
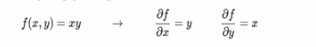
- 得到梯度
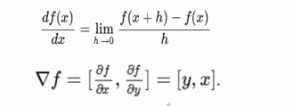
- 意义代入x=-4,y=-3
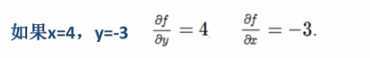
如果我们对x增加一-个小的量,对完整表达式的影响效果是?。
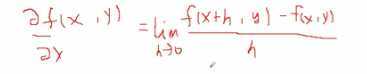
由偏导数定义,对于x增加了一个很小的量,由于得到是-3,所以对f影响是使其减少了,减少量是增加量的三倍。减少它,并且减少量是增加量的3倍。
基于每个变量的导数告诉你完整表达式在该值上的敏感度
复合函数求导数
一个函数对一个变量的导数=一个函数对中间变量的求导*中间变量对该变量的求导

例如:如果函数u=φ(t),v=ψ(t)在t可微, z=f(u,v)
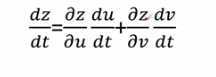
计算图
例如y=(x+y)*z可以表示成如下计算图
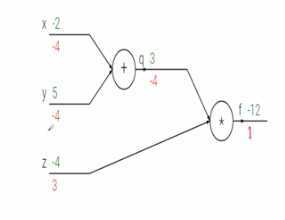
用一个计算图来表示信息的传递和导数的计算给定输入信号,我们可以立即计算出:
(1)当前节点的输出值,比如直接计算当x=-2,y=5,z=-4时候f的输出值
(2)局部梯度:当前节点的输出相对于当前节点输入的局部梯度值
- f对q求偏导数因为f=-4q,所以求偏导数是-4
- f对z丢偏导数因为f=3z ,求偏导数3
- q=(x+y),q对x和对y求偏导数为1
- 因为要求f对x求偏导数,就是df/dq乘dq/dx得到-4,f对y同理
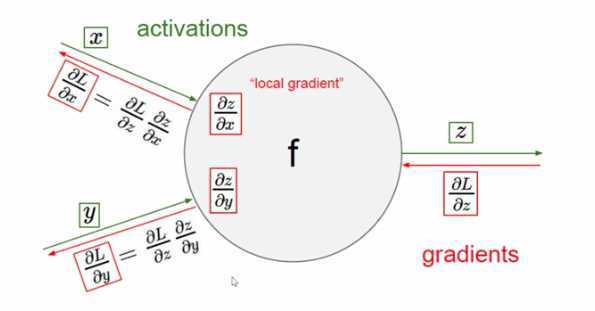
- 先计算函数相对与中间变量的梯度
- 再计算中间相对于局部变量的梯度
- 将两者一乘就得到了函数相对于局部变量的梯度
复杂例子
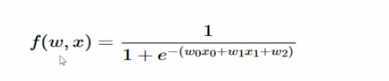
- 求导公式
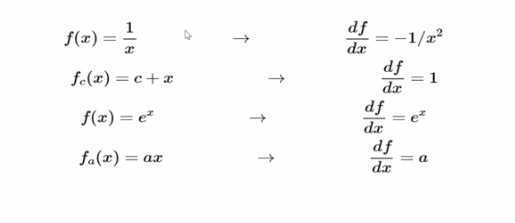
- 计算图绘制
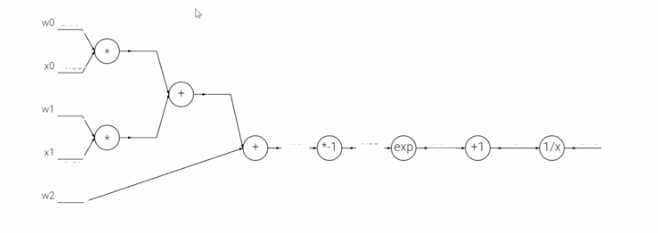
- 计算每一个节点的输出值和整体的输出值
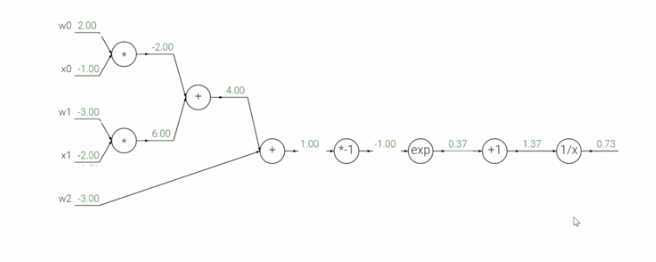
- 求导计算对每一个变量的梯度
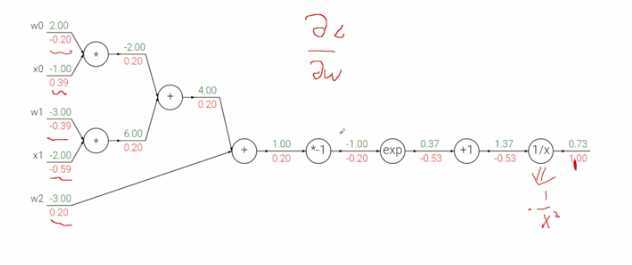
从右到左
- f相对与自身梯度一开始是1
- 1/x梯度是-1/x^2,将1.37代入 -1/(1.37)^2,再乘以1,得到-0.53
- x+1求导梯度为1,与前面相乘不变还是-0.53
- ex求导还是ex,e^-1乘以-0.53=-0.20
- -x求导得-1,乘以-0.20=0.20
- 两个变量相加,对两个变量分别求导都是1,1乘以0.20不变还是0.20
- 对于剩下两个加的节点来说,求导还是得到1,1乘以0.20不变哈市0.
- y=w0x0对w0求偏导是x0也就是-1,-1*0.20=-0.20
- y=w0x0对x0求偏导是w0也就是2, 2*0.20=0.39(近似)
- y=w1x1对w1求偏导是x1也就是-2,-2*0.20=-0.40
- y=w1x1对x1求偏导是w1也就是-3,-3*0.20=-0.60
BP算法(误差反向传播算法)
BP算法又称误差反向传播算法
主要思想:从后向前逐层传播输出层的误差,以间接算出隐层误差。.
算法分两阶段:
- (正向过程) 输入信息从输入层经隐层逐层计算各单元的输出值
- (反向传播过程)输出误差逐层向后算出隐层各单元的误差,并用此误差修正前层的权值。
通常采用梯度法修正权值,因此要求激励函数可微,一般采用logistic激励函数
前向传播

- 输入层有三个神经元、隐藏层有三个神经元、输出层有一个神经元
- 注意每层的神经元个数不包括人为添加的偏差项
- ai(j),j层第i个神经元的激活值
- θ(j),代表第j层到第j+1层网络的权值
逐层传播的过程:
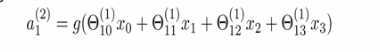
比如第二层第一个神经元的激活值=激活函数函数对之前线性变换得到的值
同理:
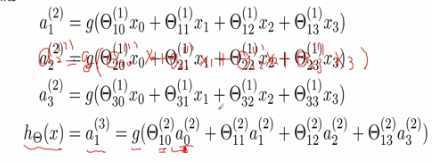
如果神经网络在第j层有Sj个神经元,j+1层有Sj+1个神经元,那么权值矩阵维度维Sj+1*(Sj+1),加一是因为偏差项
用矩阵形式来表示该过程:
- x是输入的数据

- z是线性变换得到结果
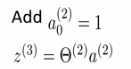
- a是对线性变换结果再经过激活函数得到的结果
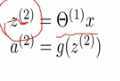
- 得到最终结果
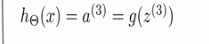
例子:包含四层神经元的神经网络:
前向传播过程:
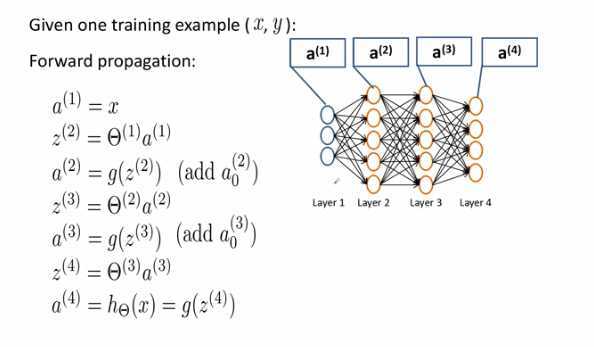
误差反向传播
我们希望计算的是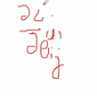 ,但是其不是很好算,有了
,但是其不是很好算,有了
这样一个偏导数,我们可以在梯度下降的过程中,更新权值
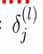 代表的是第l层第j个节点的误差
代表的是第l层第j个节点的误差
它正式的定义是误差函数cost相对于当前l层z的偏导数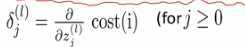
第四层的误差是,aj(4)假设输出,yj是期望输出,两者相减
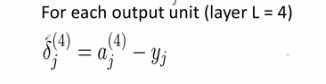
第三层的误差是:
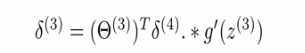
推导:
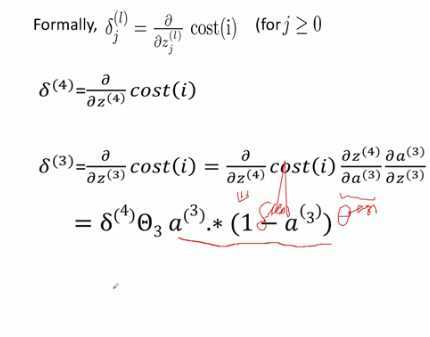
同理:
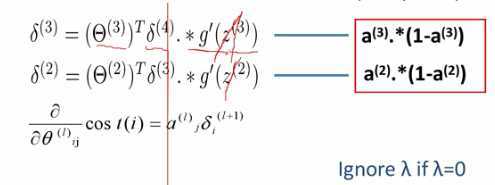
误差反向传播算法

- 对所有样本做如下计算
- 正向计算计算出每一层的输出值a
- 再通过反向传播求每一层的δ
- 对δ求平均值,还要考虑正则化项
误差前向传播与反向传播计算过程
前向传播
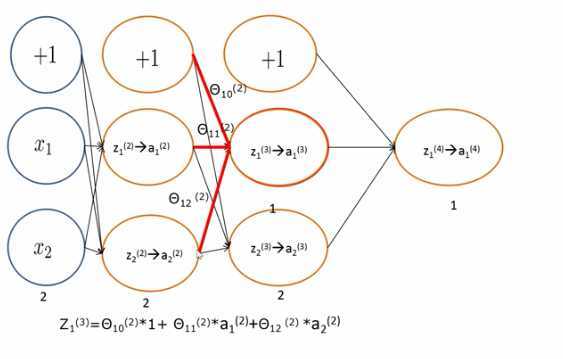
- 输入层向前传播信号,这些信号会传播给后一层的每一个神经元,线性变换得到z
- 在经过非线性变换a
- 第二层的输出值又作为下一层的输入值
- 对第二层的输入信号进行线性变换后,又进行非线性变换得到第三层的输出
- 对第三层输出值作为输入信号,输入给第四层,线性变换之后经过非线性变换得到输出
反向传播
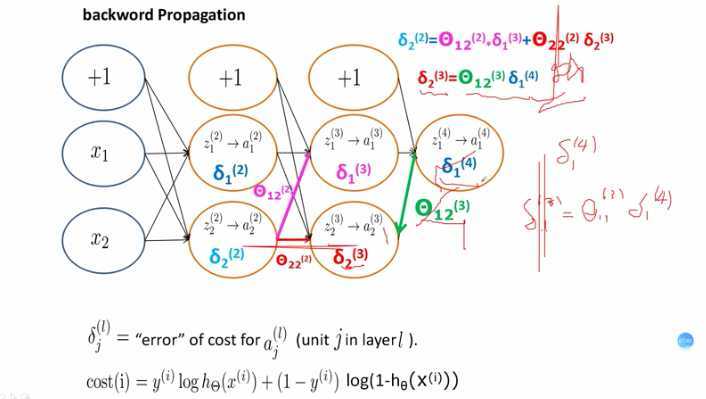
- 先计算出第四层的δ1(4)
- δ1(3)和δ2(3)可以通过公式计算

- δ2(2)可以通过公式计算得到:
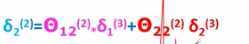
- 我们可以看到误差是如何从后向前传播的
神经网络重要性质回顾
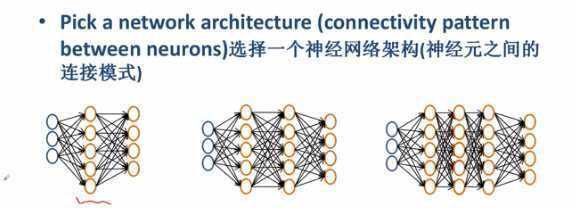
- 输入层的神经元个数对应特征的维度
- 要分多少个类输出层就对应多少个神经元
- 一个隐层用的最多,可以拟合出任何形状决策边界(有界函数)
- 多个隐层,每个隐层神经元个数都一样
- 训练网络时候,我们一开始不知道权值,会初始化权值,随机初始化权值
- 实施前向传播,计算结果
- 反向传播计算误差,更新权值
- 计算梯度容易错,所以要梯度检查
- 检查计算出梯度值与以下算式值是否接近,进行梯度检测
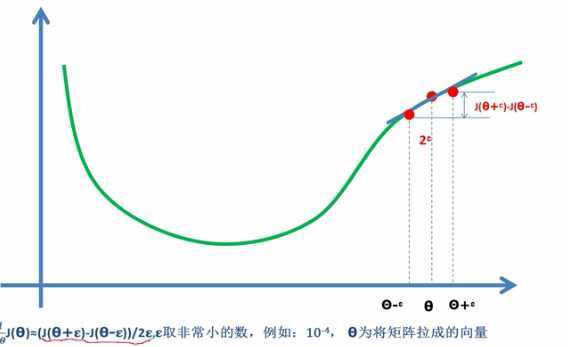

- 梯度下降更新权值,使得误差函数取得极小值
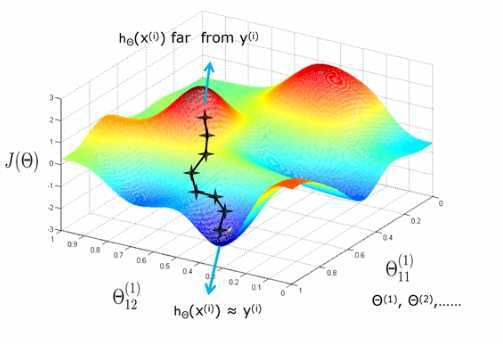
-
多层感知机是是--些全连接层的堆叠
-
利用梯度下降算法来训练(误差反向传播)
机器学习与数据分析课程笔记-分类-神经网络
原文:https://www.cnblogs.com/mengxiaoleng/p/13019575.html







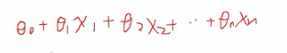
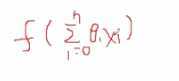
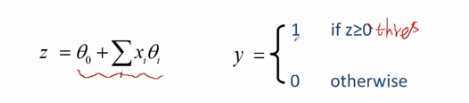












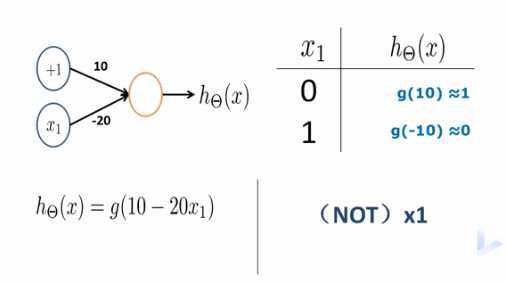
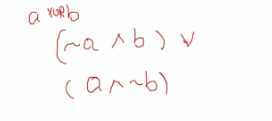
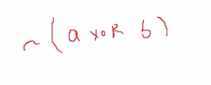







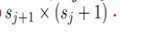
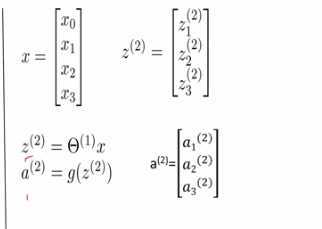
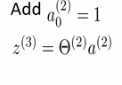
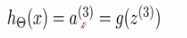






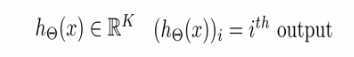


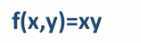
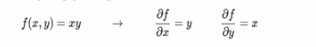
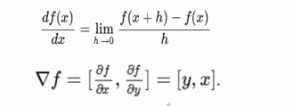
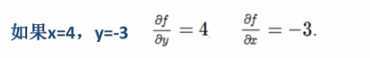
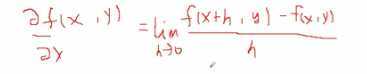

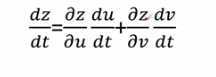


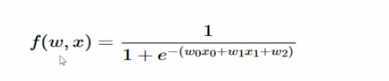
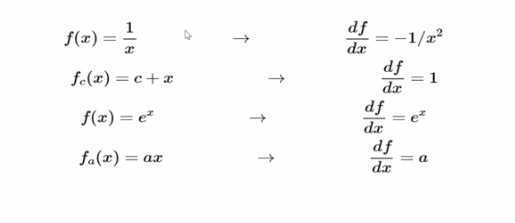




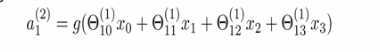
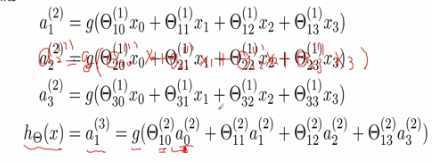

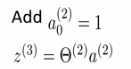
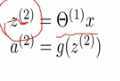
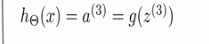

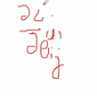 ,但是其不是很好算,有了
,但是其不是很好算,有了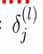 代表的是第l层第j个节点的误差
代表的是第l层第j个节点的误差