二分查找（二）

##二分查找的变形

???????二分查找虽然原理极其简单，但是想要写出没有 Bug 的二分查找并不容易。之前接触的是最简单的二分查找，即在不存在重复元素的有序数组中，查找值等于给定值的元素。

###变形1：查找第一个值等于给定值的元素

???????比如下面这样一个有序数组，其中，a[5]，a[6]，a[7]的值都等于 8，是重复的数据。我们希望查找第一个等于 8 的数据，也就是下标是 5 的元素。

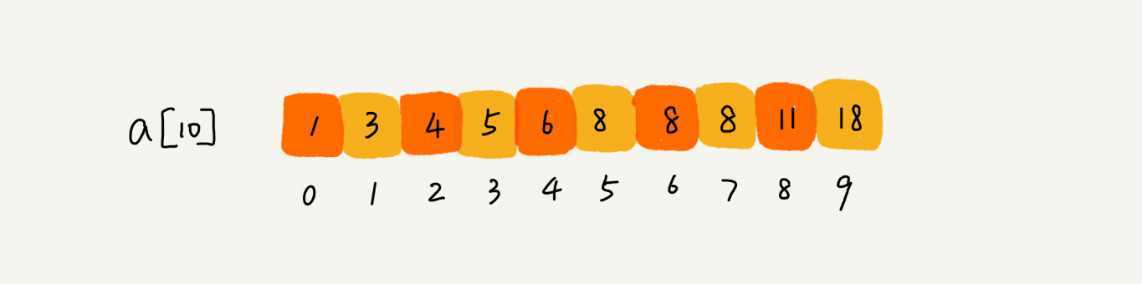
???????如果用之前的代码，那么最后返回的是最后一个8，与要求不符。

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;

  while (low <= high) {
    int mid =  low + ((high - low) >> 1);

    if (a[mid] > value) {
      high = mid - 1;
    } 
    else if (a[mid] < value) {
      low = mid + 1;
    } 
    else {
      //如果mid=0，那这个元素已经是数组的第一个元素；如果a[mid]前一个不是，那么a[mid]就是要找的
      if ((mid == 0) || (a[mid - 1] != value)) return mid;
      else high = mid - 1;
    }
  }
  return -1;
}

###变形2：查找最后一个值等于给定值的元素

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;

  while (low <= high) {
    int mid =  low + ((high - low) >> 1);

    if (a[mid] > value) {
      high = mid - 1;
    } 
    else if (a[mid] < value) {
      low = mid + 1;
    } 
    else {
      if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

###变形3：查找第一个大于等于给定值的元素

???????现在我们再来看另外一类变形问题。在有序数组中，查找第一个大于等于给定值的元素。比如，数组中存储的这样一个序列：3，4，6，7，10。如果查找第一个大于等于 5 的元素，那就是 6。

???????实际上，实现的思路跟前面的那两种变形问题的实现思路类似，代码写起来甚至更简洁。

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;

  while (low <= high) {
    int mid =  low + ((high - low) >> 1);

    if (a[mid] >= value) {
      if ((mid == 0) || (a[mid - 1] < value)) return mid;
      else high = mid - 1;
    } else {
      low = mid + 1;
    }
  }
  return -1;
}

###变形4：查找最后一个小于等于给定值的元素

public int bsearch7(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

##小结

???????凡是用二分查找能解决的，绝大部分我们更倾向于用散列表或者二叉查找树。即便是二分查找在内存使用上更节省，但是毕竟内存如此紧缺的情况并不多。

???????二分查找更适合用在“近似”查找问题，在这类问题上，二分查找的优势更加明显。

???????变体的二分查找算法写起来非常烧脑，很容易因为细节处理不好而产生 Bug，这些容易出错的细节有：终止条件、区间上下界更新方法、返回值选择。

二分查找（二）

原文：https://www.cnblogs.com/vmbn465/p/13026447.html