阅读目录

• 问题引入
• 字典树概述
• 字典树实现
• 字典树应用
• 参考资料

 一、问题引入

　　先看一道题，English Game。

　　因为之前不知道字典树是什么，所以阅读完题目后，第一时刻想到的不是用字典树存储单词，而是用数组。感觉这个题目应该要用用动态规划，但是发现因为自己考虑的是用数组存储单词，dp数组的下标意义不好确定，很难用dp，于是写了个递归算法尝试提交了一下。然后果然没过，显示内存超限，于是百度了一下题目解法后，发现这道题的正确解法是字典树+DP。

　　我：字典树？？？

二、字典树概述

1.基本概念

　　又称单词查找树，Trie树，是一中树形结构，是一种哈希树的变种。简单地说，就是用树的边表示一个字母，用根结点到其一子结点的路径表示一个单词，但由于树的存储时并没有存储边，所以字母实际上是存在子结点里的。

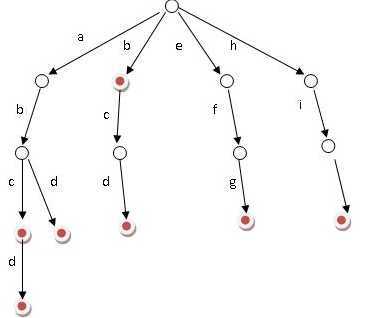
上图中带红色的节点表示该结点可以作为某一单词的结束结点，用上图我们可以很容易知道该字典树存储了7个单词（红色结点个数），分别是 abc  abcd  abd  b  bcd  efg  hij 。

2.基本性质

1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符
2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串
3. 每个节点的所有子节点包含的字符都不相同。

3.基本操作

构建树，查询单词，增加单词，删除单词。

三、字典树实现

1.结点定义

2.字典树操作

TrieNode Memory[1000000];
int allocp=0;
 
/*初始化*/
void InitTrieRoot(TrieNode* *pRoot)
{
    *pRoot=NULL;
}
 
/*创建新结点*/
TrieNode* CreateTrieNode()
{
    int i;
    TrieNode *p;
    p=&Memory[allocp++];
    p->nCount=1;
    for(i=0;i<MAX;i++)
    {
        p->next[i]=NULL;
    }
    return p;
}
 
/*插入*/
void InsertTrie(TrieNode* *pRoot,char *s)
{
    int i,k;
    TrieNode*p;
    if(!(p=*pRoot))
    {
        p=*pRoot=CreateTrieNode();
    }
    i=0;
    while(s[i])
    {
        k=s[i++]-‘a‘;//确定branch
        if(!p->next[k])
            p->next[k]=CreateTrieNode();
                else
            p->next[k]->nCount++;
        p=p->next[k];
    }
}
 
//查找
int SearchTrie(TrieNode* *pRoot,char *s)
{
    TrieNode *p;
    int i,k;
    if(!(p=*pRoot))
    {
        return0;
    }
    i=0;
    while(s[i])
    {
        k=s[i++]-‘a‘;
        if(p->next[k]==NULL) return 0;
        p=p->next[k];
    }
    return p->nCount;
}

四、字典树应用

1. 字符串检索

事先将已知的一些字符串（字典）的有关信息保存到trie树里，查找另外一些未知字符串是否出现过或者出现频率。
举例：
1，给出N 个单词组成的熟词表，以及一篇全用小写英文书写的文章，请你按最早出现的顺序写出所有不在熟词表中的生词。
2，给出一个词典，其中的单词为不良单词。单词均为小写字母。再给出一段文本，文本的每一行也由小写字母构成。判断文本中是否含有任何不良单词。例如，若rob是不良单词，那么文本problem含有不良单词。

3，1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。

2.文本预测、自动完成，see also，拼写检查

3.词频统计

1，有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。

2，一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析。

3，寻找热门查询：搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录，这些查询串的重复度比较高，虽然总数是1千万，但是如果去除重复，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就越热门。请你统计最热门的10个查询串，要求使用的内存不能超过1G。
(1) 请描述你解决这个问题的思路；
(2) 请给出主要的处理流程，算法，以及算法的复杂度。

==》若无内存限制：Trie + “k-大/小根堆”（k为要找到的数目）。

否则，先hash分段再对每一个段用hash（另一个hash函数）统计词频，再要么利用归并排序的某些特性（如partial_sort），要么利用某使用外存的方法。参考

　　“海量数据处理之归并、堆排、前K方法的应用：一道面试题” http://www.dataguru.cn/thread-485388-1-1.html。

　　“算法面试题之统计词频前k大” http://blog.csdn.net/u011077606/article/details/42640867

　　 算法导论笔记——第九章 中位数和顺序统计量 

4.排序

Trie树是一棵多叉树，只要先序遍历整棵树，输出相应的字符串便是按字典序排序的结果。
比如给你N 个互不相同的仅由一个单词构成的英文名，让你将它们按字典序从小到大排序输出。

Trie树利用多个字符串的公共前缀来节省存储空间，当我们把大量字符串存储到一棵trie树上时，我们可以快速得到某些字符串的公共前缀。

举例：
给出N 个小写英文字母串，以及Q 个询问，即询问某两个串的最长公共前缀的长度是多少？
解决方案：首先对所有的串建立其对应的字母树。此时发现，对于两个串的最长公共前缀的长度即它们所在结点的公共祖先个数，于是，问题就转化为了离线（Offline）的最近公共祖先（Least Common Ancestor，简称LCA）问题。
而最近公共祖先问题同样是一个经典问题，可以用下面几种方法：
1. 利用并查集（Disjoint Set），可以采用采用经典的Tarjan 算法；
2. 求出字母树的欧拉序列（Euler Sequence ）后，就可以转为经典的最小值查询（Range Minimum Query，简称RMQ）问题了；

6.字符串搜索的前缀匹配

trie树常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。
Trie树检索的时间复杂度可以做到n，n是要检索单词的长度，
如果使用暴力检索，需要指数级O(n²)的时间复杂度。

7.作为其他数据结构和算法的辅助结构

如后缀树，AC自动机等

后缀树可以用于全文搜索

 五、参考资料

[1] 百度百科 https://baike.baidu.com/item/Trie/140945?fr=aladdin

[2] 字典树(Trie树)实现与应用  https://www.cnblogs.com/xujian2014/p/5614724.html#_label3

[3] Trie（前缀树/字典树）及其应用  http://www.cnblogs.com/justinh/p/7716421.html

浅谈字典树（trie)

原文：https://www.cnblogs.com/x10000zhang/p/10718512.html