线性回归算法

什么是回归

1:分析 银行贷款例子

如图

2: 参数表达式

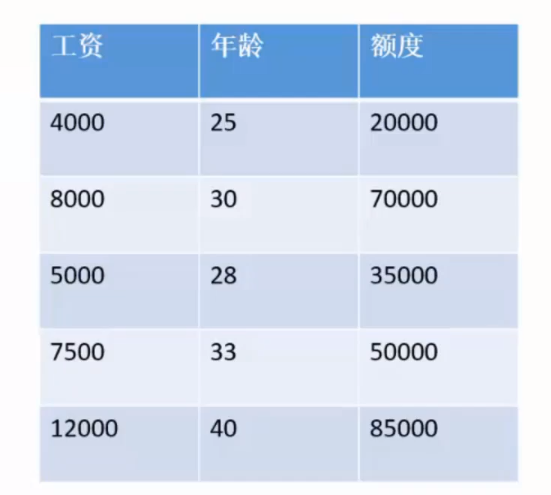
由需求可知,满足基本 基本线性设定

3:通俗解释

4:通过数学解释

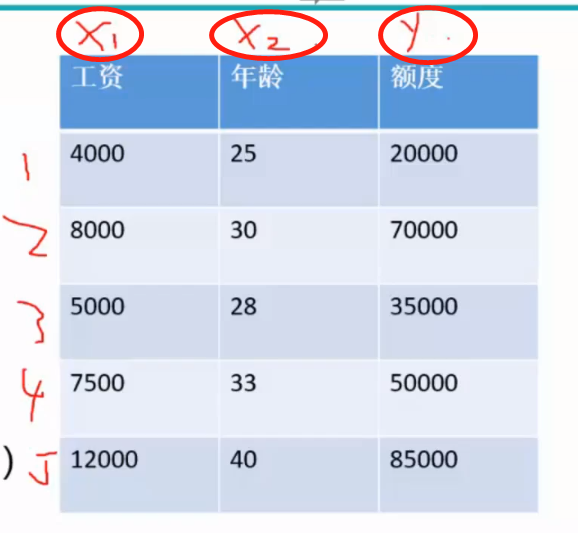
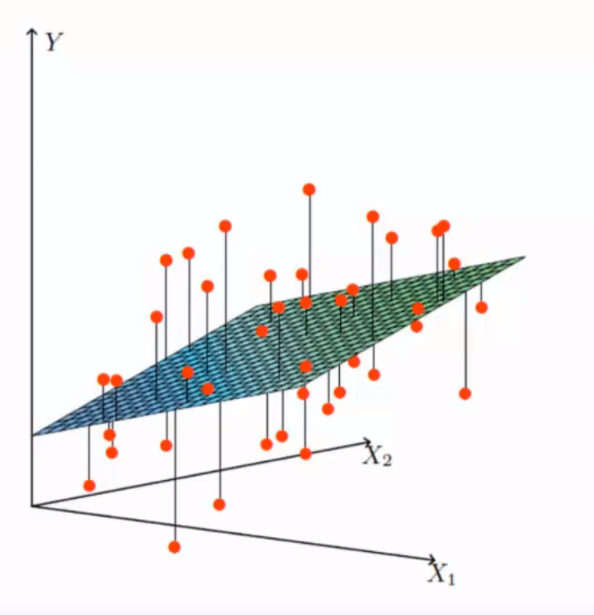
由需求可知 如果两个参数可以写成    

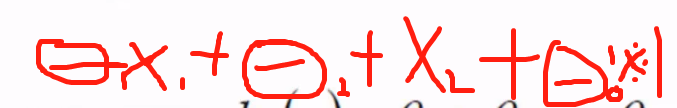
整合成数学公式为

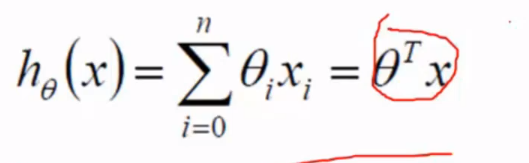
再转化成矩阵方式

5:分析误差

5.1公式假设

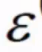为差异 , 因为理论数据与真实值 存在差异,该差异理论上可以为负数,可以为正数

5.2 误差值详解

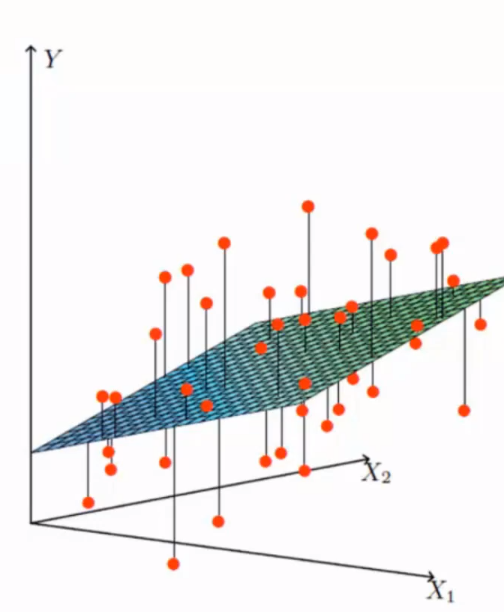
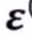 误差包括

5.3高斯分布图

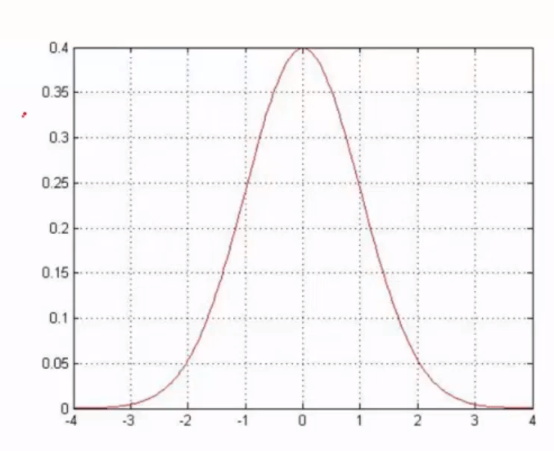
从理论上将,银行贷款的金额 普遍数据存在中间阶段 ,  数据过小,或者数据过大的概率都相对较低

5.4 讲高斯分布的误差值带入假设式

假设高斯分布的均值为0 ,即数据集满足正态分布

我们通过 y的真实值,和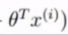的预测值, 货物误差分布的值

5.5 似然关系

假设奖品数量无线个

如:10个人抽奖,前9个人抽到1等奖 ,第10个人抽到了2等奖,那么我就可以估计 该奖品抽到的概率为90%

1: 似然函数

解释:似然函数就是 以测试样品去估计参数值 ,参数估计

即我们希望 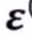为0 最好 ,

使 预测值等于真实值

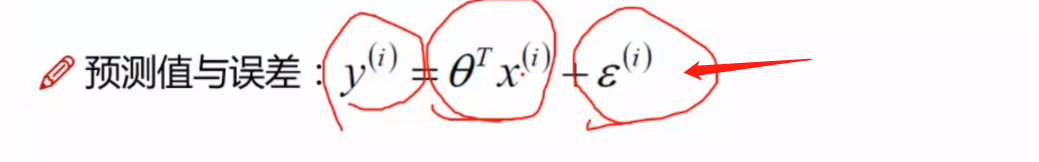
** 设定目标

我们使 测定值为真实值得概率越高越好

2:对数似然

由上述似然函数, 累乘的方式获取数据,由于累乘的方式很难计算

我们以log 取低 转成加法

3:展开化简

由上述内容可知:

我们期望 预测值值越大,越接近真实值

公式分析

取后半段变量数据

我们定义新变量

目标即为 该表达式越小越好

5.6 对公式求导求偏导取最小值

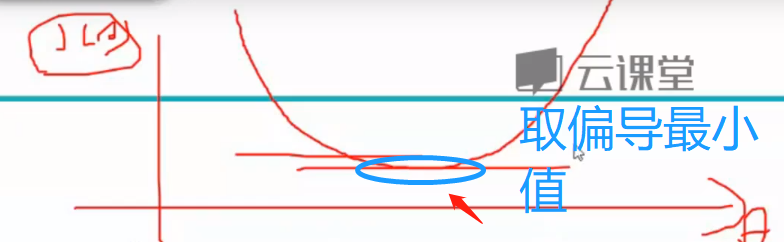
求导

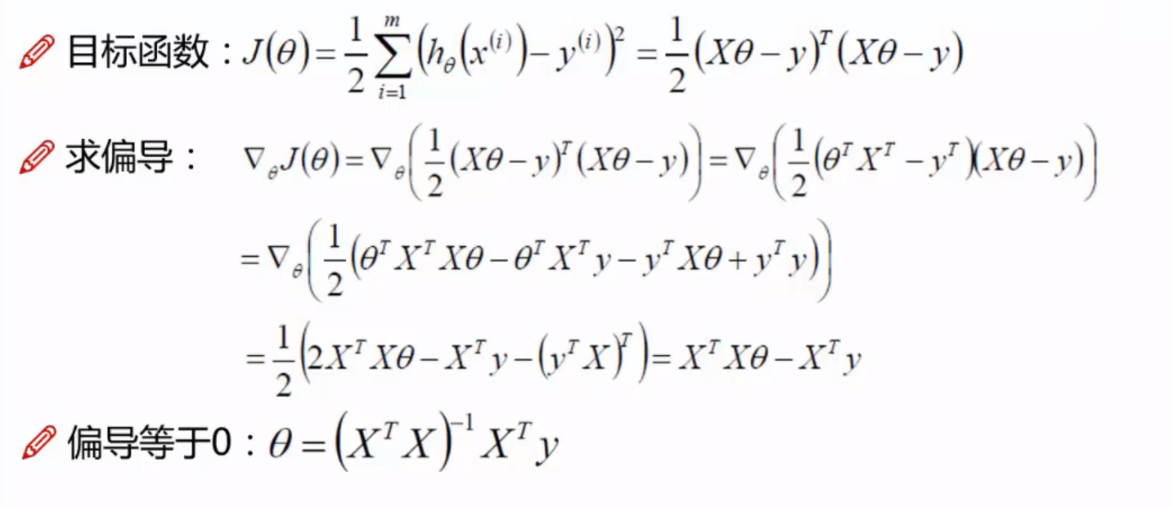
其中x为矩阵 ,y为真实值

我们通过矩阵和真实值既可以获取偏导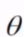 ,该值可以再一般行情况下代表数据走向

6:评估公式

6.1 :评估方法

7:梯度下降

引子:

据上述操作可以获取 偏移值 ,但是这个值不是在所有的情况下都是能求出来的.我们这里使用另外一种方式

1:引入

我们不断测试斜率 去取导数斜率最小值

2:常规套路

通过很多数据不断测试斜率 取最优值

3:如何优化

2:梯度下降详解

3:梯度下降方式

1: 目标函数

2:常规下降方式

1:批量梯度下降

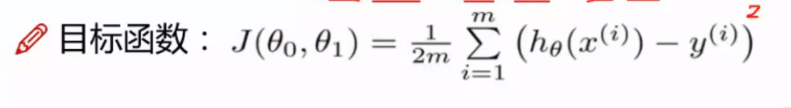
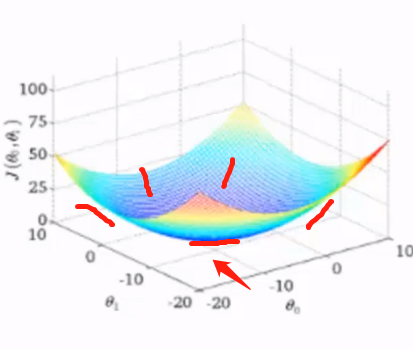
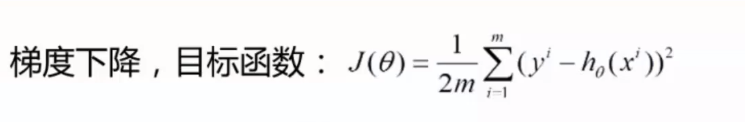
好处:精度最高

坏处:消耗资源,计算速度慢

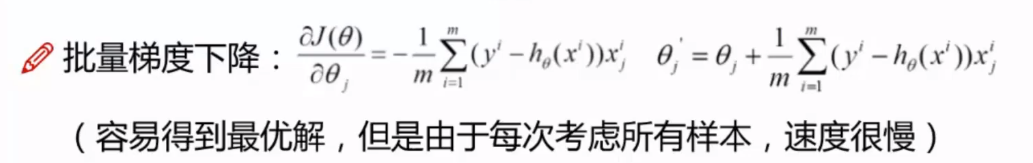
收敛方向好确定

2:随机梯度下降

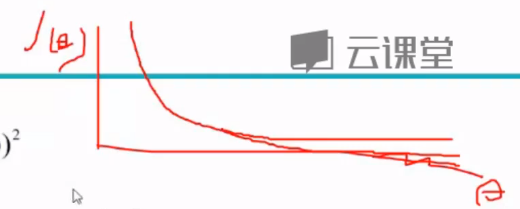
好处:计算速度快,不消耗资源

坏处:收敛方向不可控制

收敛方向随机不可控

3:小批量梯度下降法:

4: 梯度下降如何控制

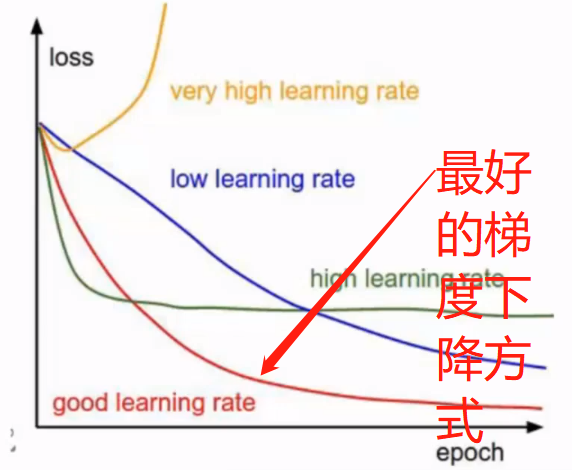
我们尽量选择最优梯度下降方案,

数据分析算法--线性回归算法讲解

原文：https://www.cnblogs.com/baili-luoyun/p/13031071.html