一、二叉搜索树(BST)
每个非叶子节点最多只有左右两个子节点。
左子节点的值 < 父节点的值
右子节点的值 > 父节点的值
层数从1开始,
1、第i层最多有2^(i-1)个节点
2、树高为i层,最多有2^i - 1 个节点
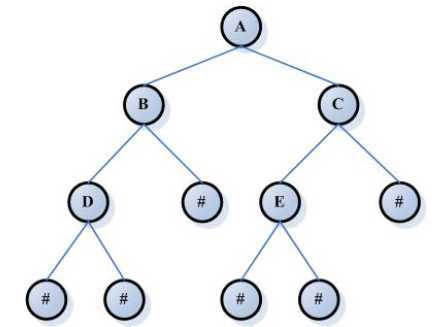
二叉搜索树的遍历:
中序遍历:父节点放在中间
前序遍历:父节点放在前面
后序遍历:父节点放在后面
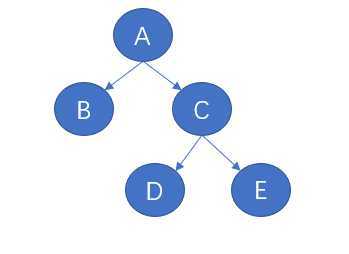
二、满二叉树
所有非叶子节点都有左右两个儿子节点,则为满二叉树
三、完全二叉树
树中每层节点从左到右依次排列。
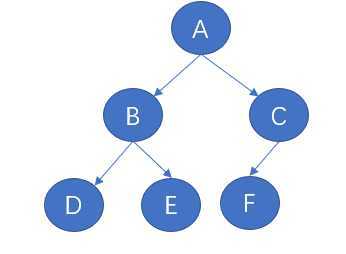
完全二叉树可用数组表示
从0开始,
第i个节点的左子节点位置->2*i+1 ;右子节点位置->2*i+2
第i个节点的父节点位置->(i-1)/2

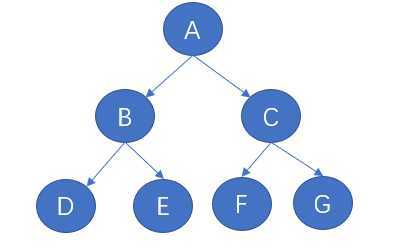
四、完美二叉树
所有的叶子节点都在最后一层
五、平衡二叉树AVL
左右两边树高最多相差1
非平衡二叉树最坏情况下退为 链表,查询和插入的时间复杂度右O(logn) -> O(n)
所以要保持树的平衡。
AVL树插入和删除动作时,会导致不平衡,此时需要通过旋转操作来保持平衡
AVL树的自平衡操作——旋转:
AVL树最关键的也是最难的一步操作就是旋转。旋转主要是为了实现AVL树在实施了插入和删除操作以后,树重新回到平衡的方法。下面我们重点研究一下AVL树的旋转。
对于一个平衡的节点,由于任意节点最多有两个儿子,因此高度不平衡时,此节点的两颗子树的高度差2.容易看出,这种不平衡出现在下面四种情况:
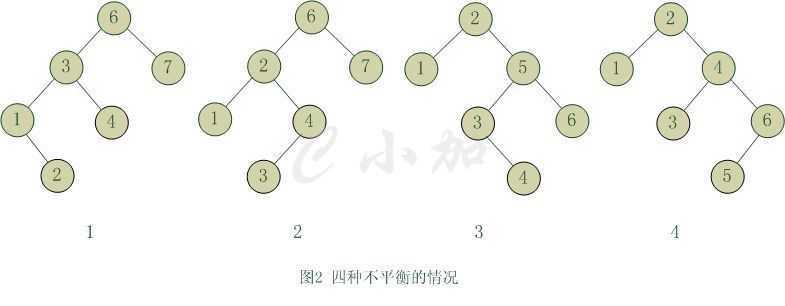
1) 6节点的左子树3节点高度比右子树7节点大2,左子树3节点的左子树1节点高度大于右子树4节点,这种情况成为左左。
2) 6节点的左子树2节点高度比右子树7节点大2,左子树2节点的左子树1节点高度小于右子树4节点,这种情况成为左右。
3) 2节点的左子树1节点高度比右子树5节点小2,右子树5节点的左子树3节点高度大于右子树6节点,这种情况成为右左。
4) 2节点的左子树1节点高度比右子树4节点小2,右子树4节点的左子树3节点高度小于右子树6节点,这种情况成为右右。
从图2中可以可以看出,1和4两种情况是对称的,这两种情况的旋转算法是一致的,只需要经过一次旋转就可以达到目标,我们称之为单旋转。
2和3两种情况也是对称的,这两种情况的旋转算法也是一致的,需要进行两次旋转,我们称之为双旋转。
单旋转
单旋转是针对于左左和右右这两种情况的解决方案,这两种情况是对称的,只要解决了左左这种情况,右右就很好办了。图3是左左情况的解决方案,节点k2不满足平衡特性,因为它的左子树k1比右子树Z深2层,而且k1子树中,更深的一层的是k1的左子树X子树,所以属于左左情况。
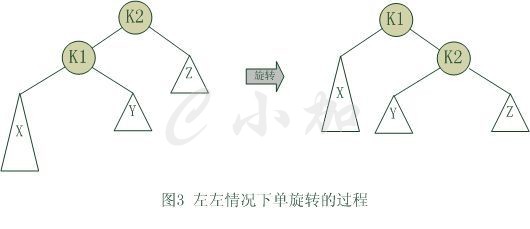
为使树恢复平衡,我们把k2变成这棵树的根节点,因为k2大于k1,把k2置于k1的右子树上,而原本在k1右子树的Y大于k1,小于k2,就把Y置于k2的左子树上,这样既满足了二叉查找树的性质,又满足了平衡二叉树的性质。
这样的操作只需要一部分指针改变,结果我们得到另外一颗二叉查找树,它是一棵AVL树,因为X向上一移动了一层,Y还停留在原来的层面上,Z向下移动了一层。整棵树的新高度和之前没有在左子树上插入的高度相同,插入操作使得X高度长高了。因此,由于这颗子树高度没有变化,所以通往根节点的路径就不需要继续旋转了。
双旋转
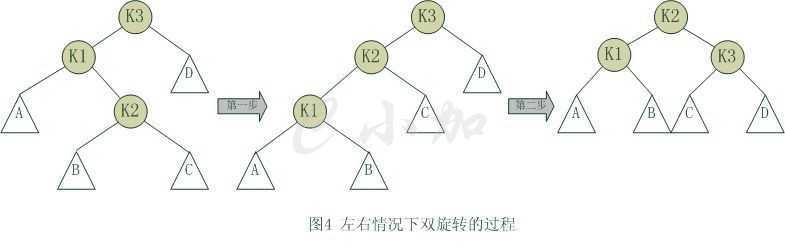
对于左右和右左这两种情况,单旋转不能使它达到一个平衡状态,要经过两次旋转。双旋转是针对于这两种情况的解决方案,同样的,这样两种情况也是对称的,只要解决了左右这种情况,右左就很好办了。图4是左右情况的解决方案,节点k3不满足平衡特性,因为它的左子树k1比右子树Z深2层,而且k1子树中,更深的一层的是k1的右子树k2子树,所以属于左右情况。
六、红黑树
红黑树也是一种平衡二叉树
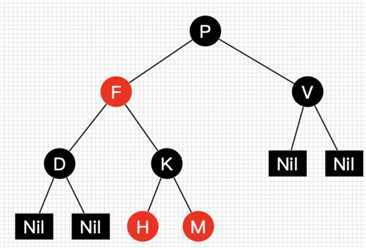
特点:
性质1. 节点是红色或黑色。
性质2. 根是黑色。
性质3. 所有叶子都是黑色(叶子是NIL节点)。
性质4. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
性质5. 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
参考:https://www.cnblogs.com/maybe2030/p/4732377.html
原文:https://www.cnblogs.com/yangfei629/p/13034493.html