1. 什么是二叉数
二叉树,字面意义是由两部分组成的树结构,更标准的定义是一个结点中最多包含两个子结点的树结构,两个子结点(node)通常被称为左子结点和右子结点。结点包含一个数据元素以及指向子结点的指针。
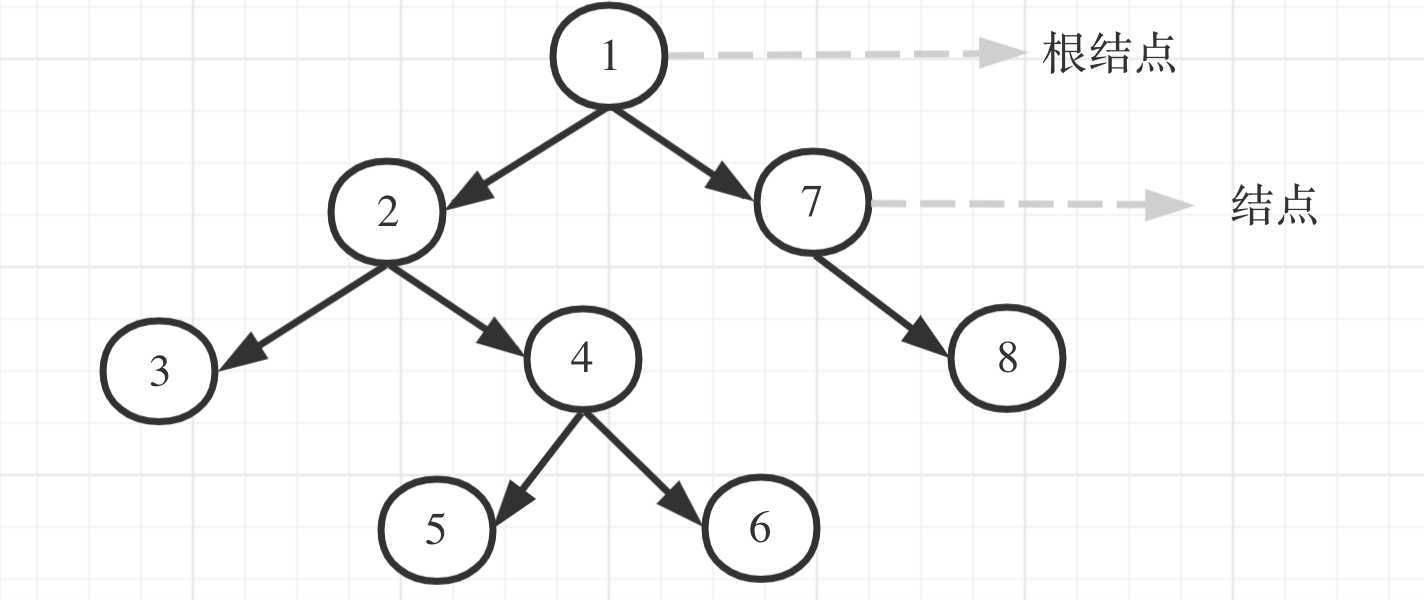
如上图所示,1是2和7的双亲结点,2和7是1的子结点,通常没有子结点的结点也会被称为叶子结点(或终端结点)。
2. 二叉树的相关概念
Node:Node可以被翻译成节点,也可以翻译成结点。一般来说,节点多指计算机网络中的物理节点,而算法中的Node通常译为结点。
结点的度(degrees):结点子树的个数。
结点的层(levels):如果根结点的层定义为1(有时候定义为0),根的子结点为第2层结点,以此类推。
树的深度:树中最大的结点层。
满二叉树(Full Binary Tree):除叶子结点的度为0外,其余所有结点的度数都为2,即每个结点都包含左子结点和右子结点。
完全二叉树(Complete Binary Tree):除了最后一层可能存在只有单独的左叶子结点之外,其余所有结点的度数都为2。(最后一层也会有左叶子结点和右叶子结点都存在的情况)
完美二叉树(Perfect Binary Tree):除叶子结点的度为0外,其余所有结点的度数都为2,并且叶子结点都在同一层。
3. 二叉树的性质
第i层的最大结点数(设根结点为第0层):2i 若根结点为第1层:2i-1
深度为h的二叉树中(设根结点为第1层),最多有 2h - 1 个结点,最少有h个结点。 若根结点为第0层,则最多有 2h+1 - 1个结点。(等比数列求和)
结点总数为N的二叉树中(设根结点为第1层),最多有 ⌊Log2n⌋+1 层 ( ⌊⌋ 为向下取整 floor),若根结点为第0层,⌊Log2n⌋ - 1 层。
4. 二叉树结构的Java代码
/*本代码来源于https://www.geeksforgeeks.org/binary-tree-set-1-introduction/ */
/* Class containing left and right child of current node and key value*/ class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } // A Java program to introduce Binary Tree class BinaryTree { // Root of Binary Tree Node root; // Constructors BinaryTree(int key) { root = new Node(key); } BinaryTree() { root = null; } public static void main(String[] args) { BinaryTree tree = new BinaryTree(); /*create root*/ tree.root = new Node(1); /* following is the tree after above statement 1 / \ null null */ tree.root.left = new Node(2); tree.root.right = new Node(3); /* 2 and 3 become left and right children of 1 1 / \ 2 3 / \ / \ null null null null */ tree.root.left.left = new Node(4); /* 4 becomes left child of 2 1 / \ 2 3 / \ / \ 4 null null null / \ null null */ } }
原文:https://www.cnblogs.com/sillymuggle/p/13029068.html