一、B树
二叉树只有最多2个分支,B树可以有多个分支,可以理解为"平衡多叉树"
B树相对二叉树在于每个节点可存储多个值,这样整体树将变得 ”矮胖“,树的高度比小,这样查询的效率就会变高。
数据库一次读操作以block为单元,一个block一般4K,我们把一个block数据尽量放入一个节点中,就避免数据库的多次IO操作
B树、B+树 多用于数据库索引。
M阶B树特点:
1、平衡
2、根节点儿子节点数 范围 [2, M]
3、非叶子节点儿子节点数 范围[M/2,M] (向上取整)
4、每个节点存储的关键字个数 = 儿子节点数 - 1
5、每个节点的关键字、以及儿子节点 从小到大 排序
6、所有叶子节点在同一层
数据的存储
每个节点不仅仅存储关键字,还保持每个关键字指向实际数据的指针
B+的平衡:通过关键字的拆分、合并操作实现平衡
比如我们要在下图中插入元素4:
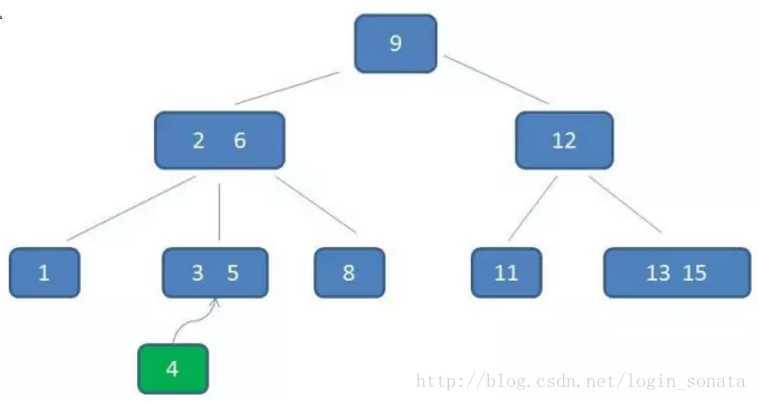
1,首先自顶向下查询找到4应该在的位置,即3、5之间;
2,但是3阶b树的节点最多只能有2个元素,所以把3、4、5里面的中间元素4上移(中间元素上移是插入操作的关键);
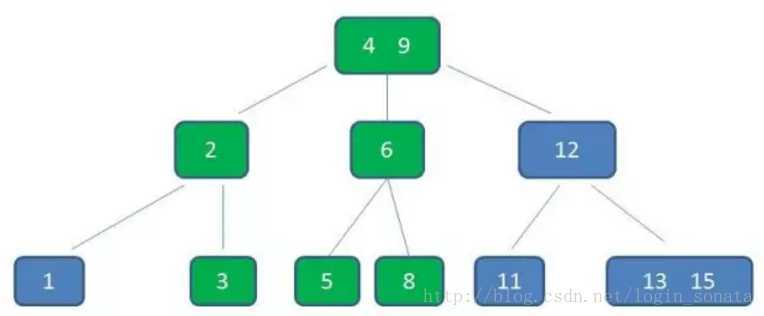
3,上一层节点加入4之后也超载了,继续中间元素上移的操作,现在根节点变成了4、9;
4,还要满足查找树的性质,所以对元素进行调整以满足大小关系,始终维持多路平衡也是b树的优势,最后变成这样:
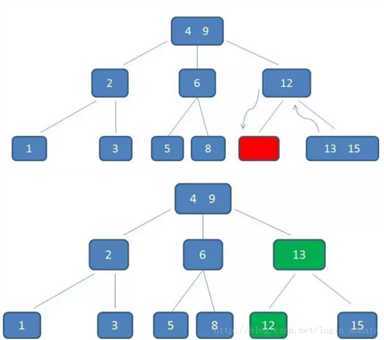
再比如我们要删除元素11:
1,自顶向下查询到11,删掉它;
2,然后不满足b树的条件了,因为元素12所在的节点只有一个孩子了,所以我们要“左旋”,元素12下来,元素13上去:
二、B+树
在B树的基础上,有如下变化
1、节点的关键字个数=儿子节点数
2、叶子节点保持所有的关键字,且用指针相连
3、非叶子节点只保存关键字,不再保存数据,所以可以有更多的空间存放关键字,更加 “矮胖“
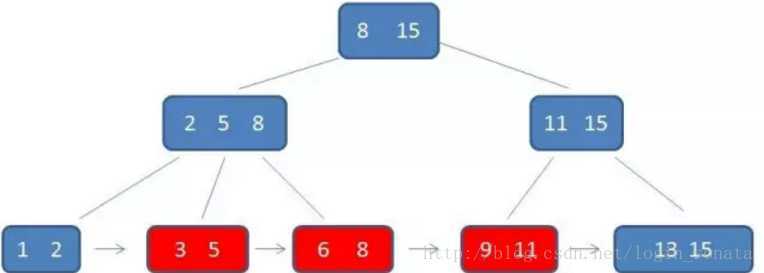
数据存储
只有叶子节点存储数据,非叶子节点只存关键字用作索引
三、对比
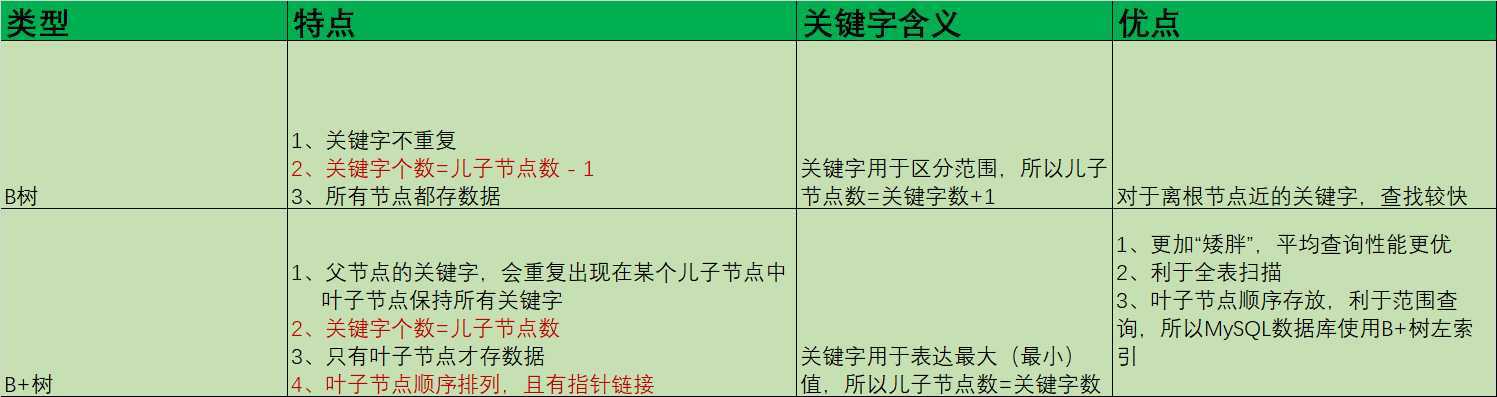
参考: https://blog.csdn.net/login_sonata/java/article/details/75268075
原文:https://www.cnblogs.com/yangfei629/p/13047047.html