1.题目

Given two strings representing two complex numbers.

You need to return a string representing their multiplication. Note i2 = -1 according to the definition.

Example 1:
Input: "1+1i", "1+1i"
Output: "0+2i"
Explanation: (1 + i) * (1 + i) = 1 + i2 + 2 * i = 2i, and you need convert it to the form of 0+2i.
Example 2:
Input: "1+-1i", "1+-1i"
Output: "0+-2i"
Explanation: (1 - i) * (1 - i) = 1 + i2 - 2 * i = -2i, and you need convert it to the form of 0+-2i.
Note:

The input strings will not have extra blank.
The input strings will be given in the form of a+bi, where the integer a and b will both belong to the range of [-100, 100]. And the output should be also in this form.

2.思考点

这道题不难，只要将数学表达式展开然后拆解字符串就可以了。

    public String complexNumberMultiply(String a, String b) {
        String string = a.split("\\+")[0];
        int num1 = Integer.valueOf(a.split("\\+")[0]);
        int num2 = Integer.valueOf(a.split("\\+")[1].substring(0,a.split("\\+")[1].length()-1));
        int num3 = Integer.valueOf(b.split("\\+")[0]);
        int num4 = Integer.valueOf(b.split("\\+")[1].substring(0,b.split("\\+")[1].length()-1));
        return (num1*num3 + num2*num4*(-1)) + "+" + (num2*num3 + num1*num4) + "i";     
    }

这个是我最开始的解法，用加号来拆解字符串，然后用substring将i拆解出来。然后在我看solution时发现正则表达式中的“|”代表或，那么这里就有另一种方法

    public String complexNumberMultiply(String a, String b) {
        String string = a.split("\\+|i")[0];
        int num1 = Integer.valueOf(a.split("\\+|i")[0]);
        int num2 = Integer.valueOf(a.split("\\+|i")[1]);
        int num3 = Integer.valueOf(b.split("\\+|i")[0]);
        int num4 = Integer.valueOf(b.split("\\+|i")[1]);
        return (num1*num3 + num2*num4*(-1)) + "+" + (num2*num3 + num1*num4) + "i";
    }

我们可以明显的发现，全部使用正则表达式来拆解字符串效率会低很多，接着大家可以参考这篇文章https://yq.aliyun.com/articles/292304。

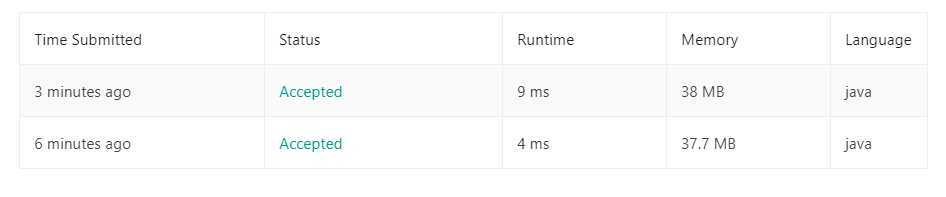
我们可以发现，正则表达式实际效率是很低的，如果要进行普通的字符串操作，推荐使用Apache Commons Lang这个包。

【LeetCode】537. Complex Number Multiplication

原文：https://www.cnblogs.com/Oliver1993/p/13049717.html