总目录 > 8 图论 > 8.3 最小生成树
前言
子目录列表
8.4 拓扑排序与关键路径
1、DAG 与 AOV 网
一个无环的有向图被称作有向无环图(DAG,Directed Acycline Graph)。它不同于有向树,DAG 将有向边改成无向边后可以出现环,而有向树不行。
DAG 应用广泛,除了在动态规划中提到了 4.4 树形 / DAG / 数位 DP ,它往往是描述一项工程或系统进行过程的有效工具。所有的大型工程(Project)都可以被划分为若干个子工程,这些子工程被称作活动(Activity)。在整个工程中,有些活动必须在其他相关活动完成后才能开始,也就是说,一个活动的开始是以其所有前序活动的完工为先决条件。部分活动没有先决条件,则可以随时开始。人们关心这个工程是否能够顺利进行,如果能,如何安排工程完成的先后顺序使得所花费时间最短,而 DAG 正是形象反映出整个工程的活动之间的约束关系的最佳选择。
我们以顶点表示活动,有向边表示活动之间的约束关系,这样的 DAG 被称作顶点活动网(AOV 网,Activity On Vertex Network)。
2、拓扑排序
根据上述对 AOV 网的定义,我们先来举个例子。
杰克对计算机很感兴趣,进入大学后他如愿以偿地进修计科专业。学校发给他一份培养方案,上面写满了各种课程:
课程代号 课程名称 先修课程
C1 高等数学 无
C2 C 程序设计 无
C3 离散数学 C1, C2
C4 数据结构 C3, C5
C5 C++ 程序设计 C2
C6 编译技术 C4, C5
C7 操作系统 C4, C9
C8 大学物理 C1
C9 计算机组成 C8
杰克表示头都晕了,他想理清楚这些课程的关系。这时候,使用一张 AOV 网来展示:
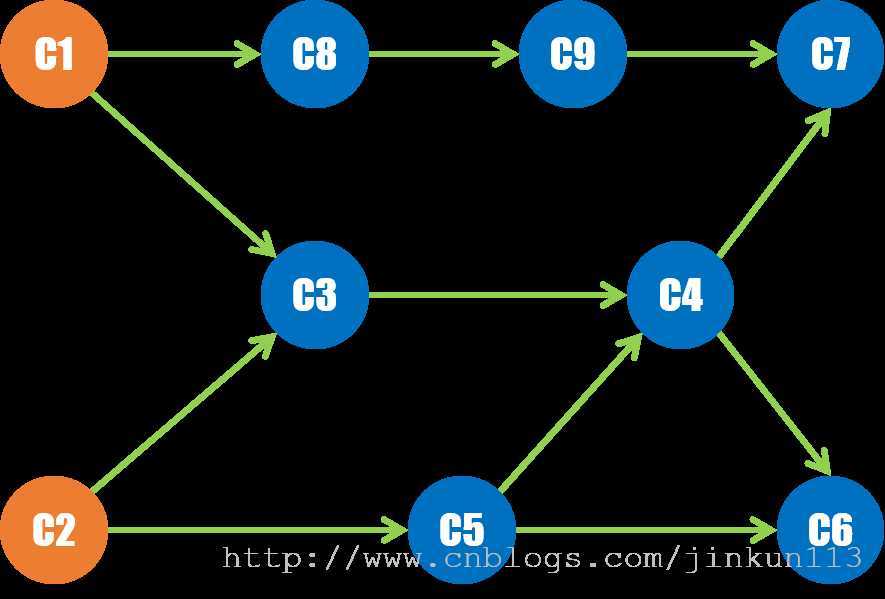
原文:https://www.cnblogs.com/jinkun113/p/13057781.html