一、二分法查找介绍

• 二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。
• 每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为0。

1.1、二分法查找的时间复杂度

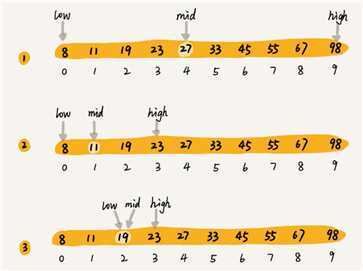
• 我们假设数据大小是 n，每次查找后数据都会缩小为原来的一半，也就是会除以2。最坏情况下，直到查找区间被缩小为空，才停止。

• 

• 这是一个等比数列。其中 n/2^k = 1 时， k 的值就是总共缩小的次数。

• 而每一次缩小操作只涉及两个数据的大小比较，所以，经过了 k 次区间缩小操作，时间复杂度就是 O(k)。通过 n/2^k = 1，我们可以求得 k= log2n，所以时间复杂度就是 O(logn)。

• O(logn) 这种对数时间复杂度。这是一种极其高效的时间复杂度，有的时候甚至比时间复杂度是常量级 O(1) 的算法还要高效。

• 因为 logn 是一个非常“恐怖”的数量级，即便 n 非常非常大，对应的 logn 也很小。

• 比如 n 等于2的32次方，这个数大约是42亿。也就是说，如果我们在 42 亿个数据中用二分查找一个数据，最多需要比较32次。

• 大 O 标记法表示时间复杂度的时候，会省略掉常数、系数和低阶。

• 对于常量级时间复杂度的算法来说， O(1) 有可能表示的是一个非常大的常量值，比如 O(1000)、 O(10000)。

• 所以，常量级时间复杂度的算法有时候可能还没有 O(logn) 的算法执行效率高。

• 反过来，对数对应的就是指数。指数时间复杂度的算法在大规模数据面前是无效的。

1.2、二分法的实现

1、非递归实现

/**
 * 二分法查找，非递归实现
 *
 * @param arr
 * @param a
 * @return
 */
public static int binarySearch(int[] arr, int a) {
    int start = 0;
    int end = arr.length - 1;

    while (start <= end) { // 不能是start < end
        int mid = start + ((end - start) >> 1); //start + (end - start)/2 位运算符速度快
        if (arr[mid] == a) {
            return mid;
        } else if (arr[mid] > a) {
            end = mid - 1; // end = min 有时会造成死循环
        } else {
            start = mid + 1;
        }
    }
    return -1;
}

2、递归实现

/**
 * 二分法递归实现
 *
 * @param arr
 * @param start
 * @param end
 * @param a
 * @return
 */
public static int binarySearch2(int[] arr, int start, int end, int a) {
    if (start > end) return -1;
    int mid = start + ((end - start) >> 1);
    if (arr[mid] == a) {
        return mid;
    } else if (arr[mid] > a) {
        end = mid - 1;
        return binarySearch2(arr, start, end, a);
    } else {
        start = mid + 1;
        return binarySearch2(arr, start, end, a);
    }
}

二、二分法查找的局限性

二分查找的时间复杂度是O(logn)，查找数据的效率非常高。不过，并不是什么情况下都可以用二分查找，它的应用场景是有很大局限性的。

• 首先，二分查找依赖的是顺序表结构，就是数组。

  • 二分查找不能依赖链表。原因二分查找算法需要按照下标随机访问元素。
  • 数组按照下标随机访问数据的时间复杂度是 O(1)，而链表随机访问的时间复杂度是 O(n)。
  • 所以，如果数据使用链表存储，二分查找的时间复杂就会变得很高。
  • 二分查找只能用在数据是通过顺序表来存储的数据结构上。如果你的数据是通过其他数据结构存储的，则无法应用二分查找。

• 二分查找针对的是有序数据。

  • 二分查找对这一点的要求比较苛刻，数据必须是有序的。如果数据没有序，我们需要先排序。
  • 序的时间复杂度最低是 O(nlogn)。所以，如果针对的是一组静态的数据，没有频繁地插入、删除，我们可以进行一次排序，多次二分查找。
  • 这样排序的成本可被均摊，二分查找的边际成本就会比较低。
  • 如果数据集合有频繁的插入和删除操作，要想用二分查找，要么每次插入、删除操作之后保证数据仍然有序，要么在每次二分查找之前都先进行排序。
  • 针对这种动态数据集合，无论哪种方法，维护有序的成本都是很高的。
  • 所以，二分查找只能用在插入、删除操作不频繁，一次排序多次查找的场景中。针对动态变化的数据集合，二分查找将不再适用。

• 数据量太大也不适合二分查找。

  • 二分查找的底层需要依赖数组这种数据结构，而数组为了支持随机访问的特性，要求内存空间连续，对内存的要求比较苛刻。
  • 比如，有 1GB 大小的数据，如果希望用数组来存储，那就需要 1GB 的连续内存空间。
  • 注意这里的“连续”二字，也就是说，即便有 2GB 的内存空间剩余，但是如果这剩余的 2GB 内存空间都是零散的，没有连续的 1GB 大小的内存空间，那照样无法申请一个1GB大小的数组。
  • 而二分查找是作用在数组这种数据结构之上的，所以太大的数据用数组存储就比较吃力了，也就不能用二分查找了。

五、二分法查找

原文：https://www.cnblogs.com/xiexiandong/p/13057633.html