算法思想:https://www.bilibili.com/video/BV1Ut41197NX?t=715
一,比较
Dijkstra : 是一种解决单源最短路径的算法,即 固定一点到 余下所有点的最短路径
当若 我们要求所有点之间的最短路径呢?
一个方法是:将 Dij 用 n 次,不过这个时间复杂度一下子就到 n的3次方
于是,有人想出了 Floyd 想出了 Floyd算法
Floyd: 解决所有顶点间的最短路径
二,步骤
1,初始化
用 邻接矩阵 ,对角线全为 0
若存在 <vi,vj>, 则为其权值,否则为 无穷大
2,试探
试着在所有路径中,加入中间顶点 Vx,
若路径变小,则改邻接矩阵的值;否则不变
3,循环
试探完所有顶点,算法结束
三,例题
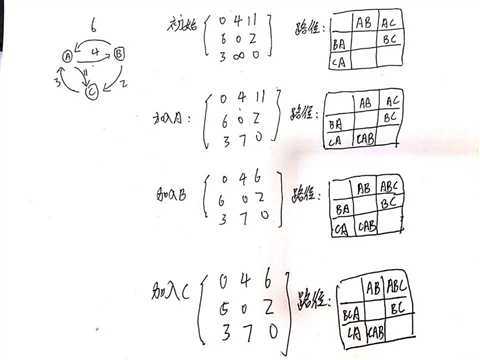
四,代码

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define MIN(x,y) (((x)<(y))?(x):(y)) #define inf 0x3f3f3f3f #define N 105 int a[N][N]; int n; void show() { puts(""); for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { printf("%d ", a[i][j]); }puts(""); } } int main(void) { scanf("%d", &n); for (int i = 1; i <= n; i++) //1,初始化 用 邻接矩阵 ,对角线全为 0 若存在 <vi, vj>, 则为其权值,否则为 无穷大 { for (int j = 1; j <= n; j++) a[i][j] = inf; a[i][i] = 0; } int m; scanf("%d", &m); // 边数 while (m--) { int x, y, w; scanf("%d%d%d", &x, &y, &w); a[x][y] = w; } for (int k = 1; k <= n; k++) // 3,循环 试探完所有顶点,算法结束 { for (int i = 1; i <= n; i++) // 2,试探 试着在所有路径中,加入中间顶点 Vx , 若路径变小,则改邻接矩阵的值;否则不变 { for (int j = 1; j <= n; j++) { a[i][j] = MIN(a[i][j], a[i][k] + a[k][j]); } } } show(); system("pause"); return 0; }/* 3 5 1 2 4 2 1 6 1 3 11 3 1 3 2 3 2 */
注意:这里没有存路径
这里的测试数据是上面那个例题。
=========== ======== ========= ======= ====== ===== ==== === == =
If there‘s any kind of magic in the world, it must be the attempt of understanding someone or share something.
—Before Sunrise
其实最让我们挣扎、绝望的不是困难,而是身边没有一个值得相信的朋友,能让我敞开心扉跟他分享!
原文:https://www.cnblogs.com/asdfknjhu/p/13060731.html