在之前描述的AVL树中,对于删除某个元素导致树不平衡的情况,需要进行旋转调整,使之恢复平衡。然而,该过程可能需要沿着parent关系经历O(logn)次旋转操作才可使得整棵树平衡。因此,在此基础上设计出来另外一种数据结构--红黑树,它的添加和删除的旋转操作都是O(1)级别,但需要牺牲一些平衡性。
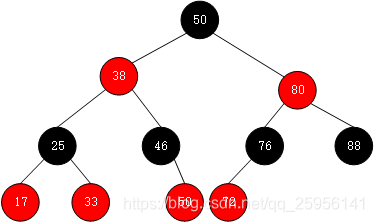
文章省略了对于B树,AVL树的一些性质和操作的描述,可参考AVL树、B树。
红黑树需满足以下几条性质:
红黑树继承于二叉排序树,因此其查找方式和二叉排序树相同。另外,对于结点的旋转,获取前驱后继等操作本文不再赘述,可参考前面的章节:AVL树。
我们对添加的元素默认设置为RED颜色,有可能破坏红黑树的性质,分为以下几种情况,对其进行相应的调整:
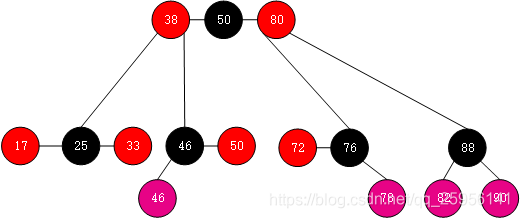
由于红黑继承二叉排序树,因此在删除节点后,如果删除的是度为2的结点,会选择其前驱或者后继来代替被删除的节点,因此最终删除的结点在其转换成B树形式后的叶子节点中,可参考二叉排序树、B树。
删除节点为RED:直接删除,无需做任何调整。
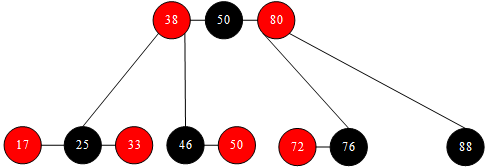
如删除途中的17、33、50、72结点。再如,删除38,则会选择其前驱33替换38,最终删除的结点为33。
删除节点为BLACK,并且只有1RED个孩子:在二叉排序树中,这种情况不存在其还有2个孩子的情况,原因是会继续向下寻找被删除节点的前驱或后继。因此被删除的节点如果是BLACK,其只可能存在一个孩子或者没有孩子的情况,而且如果有孩子,这个孩子的颜色必定为RED,原因是如果为BLACK,将会破坏红黑树的性质:从根节点到叶子节点的所有路径上不能有2个连续的RED节点。对于上述情况,只需将其孩子替换当前节点,并将其染BLACK即可。
-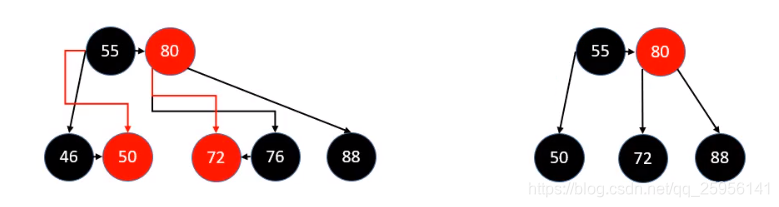
上图描述了删除46、76的示意图。
删除节点为BLACK,并且没有孩子:即删除的节点为BLACK叶子结点的情况。从B树角度可知(性质8),删除元素后造成下溢,进而对其进行下溢调整。下溢调整有如下几种情况:
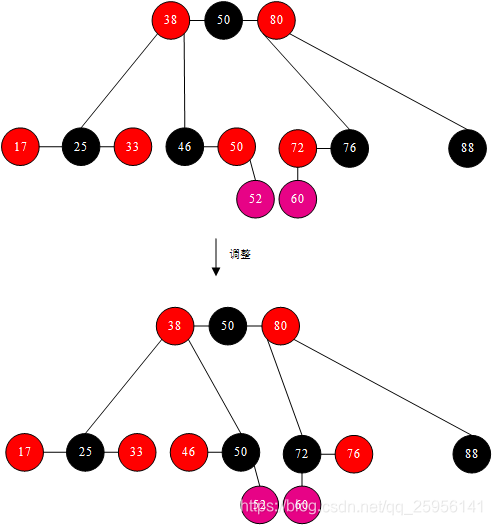
1)兄弟节点有多余的红孩子,则可向兄弟节点借一个元素,则只需进行旋转操作即可,如图删除节点88,进行兄弟节点76可借,对80进行LR调整,调整后,上面的节点跟随parent原来的颜色,左右孩子染BLACK,进而得到下图所示。
 2)兄弟节点没有多余的RED节点,则无法借元素,则只需将parent染BLACK,兄弟节点染成RED即可。当parent原来也是BLACK时,则相当于将原来的parent代替了被删除节点的位置,此时发生下溢,进一步把parent也当成被删除节点处理即可。
2)兄弟节点没有多余的RED节点,则无法借元素,则只需将parent染BLACK,兄弟节点染成RED即可。当parent原来也是BLACK时,则相当于将原来的parent代替了被删除节点的位置,此时发生下溢,进一步把parent也当成被删除节点处理即可。
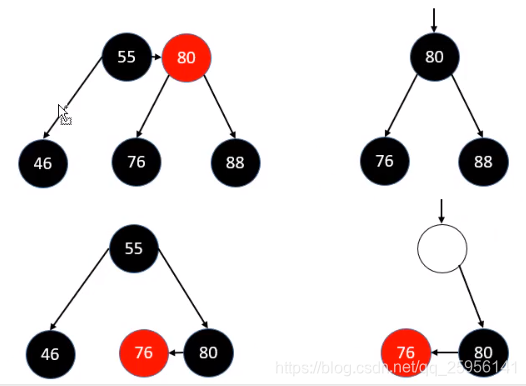
上图所示删除88后,将80染黑,76染红,恢复红黑树性质。但当80本身为BLACK时,删除88进行上述操作,相当于将80代替了原来88的位置,造成下溢。
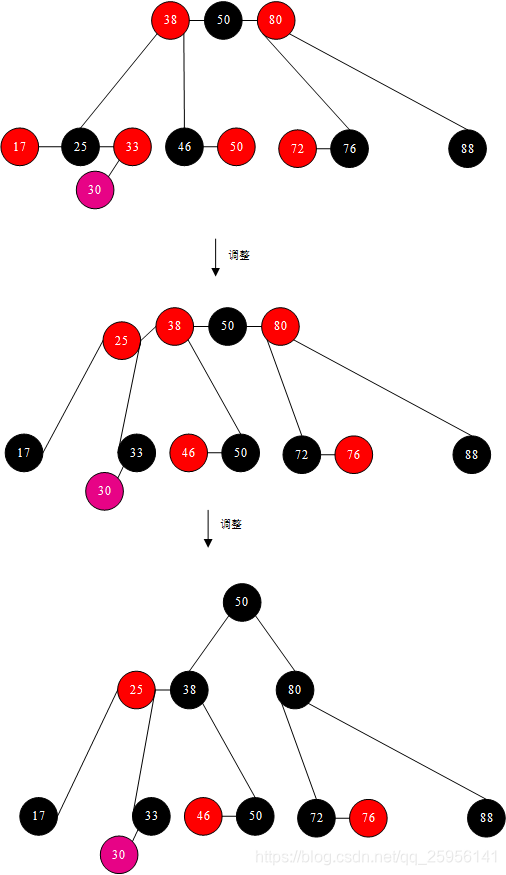
3)兄弟节点为RED结点,在B树角度,兄弟节点应该为BLACK节点。兄弟节点染BLACK,parent节点染成RED,旋转改变兄弟节点,之后回到上述1)2)中的情况。
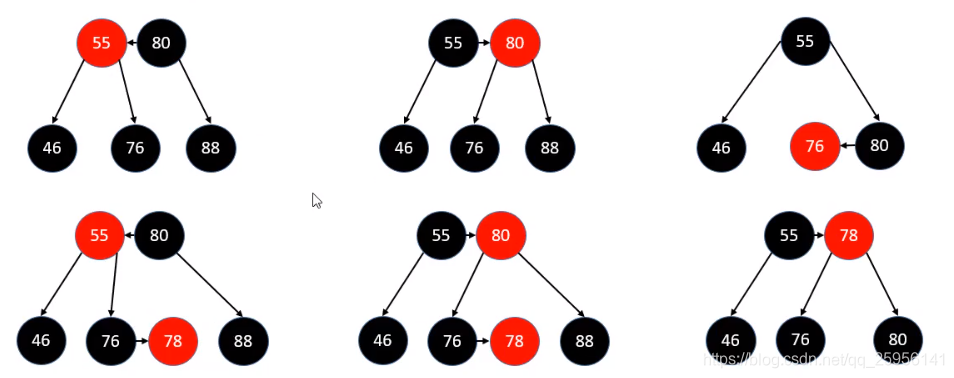
上图所示删除88,但兄弟节点55位红,将其染黑,父节点80染红,之后旋转调整76为其兄弟,之后进行1)或2)的操作即可。
本节使用Java语言描述红黑树数据结构,由于红黑树继承于平衡二叉搜索树,并在之前的AVL树、平衡二叉搜索树博客中有描述,这里不在赘述。
基于二叉排序树结点,增加color属性。
private static class RBNode<E> extends Node<E>{
boolean color = RED;
public RBNode(E element,Node<E> parent){
super(element,parent);
}
}
public class RBTree<E> extends BBSTree<E> {
private static final boolean RED = false;
private static final boolean BLACK = true;
public RBTree(){
this(null);
}
public RBTree(Comparator<E> comparator){
super(comparator);
}
/**
* 将节点染成对应的颜色
* @param node
* @param color
* @return
*/
private Node<E> color(Node<E> node,boolean color){
if(node == null){
return node;
}
((RBNode<E>)node).color = color;
return node;
}
private Node<E> red(Node<E> node){
return color(node,RED);
}
private Node<E> black(Node<E> node){
return color(node,BLACK);
}
/**
* 查看某个节点的颜色
* @param node
* @return
*/
private boolean colorOf(Node<E> node){
//空节点默认为黑色
return node == null?BLACK:((RBNode<E>)node).color;
}
/**
* 是否为黑色节点
* @param node
* @return
*/
private boolean isBlack(Node<E> node){
return colorOf(node) == BLACK;
}
/**
* 是否为红色节点
* @param node
* @return
*/
private boolean isRed(Node<E> node){
return colorOf(node) == RED;
}
@Override
protected Node<E> createNode(E element,Node<E> parent) {
return new RBNode<>(element,parent);
}
}
添加情况参考2.2。
@Override
protected void afterAdd(Node<E> node) {
Node<E> parent = node.parent;
//添加的是根结点
if(parent == null){
black(node);
return;
}
//添加的父结点是黑色
if(isBlack(parent)) return;
Node<E> uncle = parent.sibling();
Node<E> grand = parent.parent;
if(isRed(uncle)){ //B树上溢
black(parent);
black(uncle);
red(grand);
afterAdd(grand);
return;
}
//叔父结点不是红色的情况
if(parent.isLeftChild()){
if(node.isLeftChild()){ //LL
black(parent);
red(grand);
rotateRight(grand);
}else{ //LR
black(node);
red(grand);
red(parent);
rotateLeft(parent);
rotateRight(grand);
}
}else{
if(node.isRightChild()){ //RR
black(parent);
red(grand);
rotateLeft(grand);
}else{ //RL
black(node);
red(grand);
red(parent);
rotateRight(parent);
rotateLeft(grand);
}
}
}
删除情况较为复杂,参考2.3的详细操作流程。
@Override
protected void afterRemove(Node<E> node,Node<E> replacement) {
//被删除的结点只会发生在最后一层,即使不是叶子结点也没关系
if(isRed(node)){
return;
}
//用于取代的node结点是红色,自身肯定不会是红色,因为不可能Double red
if(isRed(replacement)){
black(replacement);
return;
}
//来到这里一定是叶子结点
//删除的结点是黑色
Node<E> parent = node.parent; //parent没有断
if(parent == null){ //被删除的是根结点
return;
}
boolean left = parent.left == null || node.isLeftChild();
//由于在儿叉排序树中会断掉left或者right,则根据left或者right是否为空的情况判定自身为left或right
Node<E> sibling = left? parent.right : parent.left;
if(left){ //被删除的结点在左边,兄弟节点在右边,左右操作对称
if(isRed(sibling)){ //兄弟节点是红色,将其转换成兄弟节点是黑色的情况
black(sibling);
red(parent);
rotateLeft(parent);
sibling = parent.right;
}
//兄弟节点是黑色
if(isBlack(sibling.left) && isBlack(sibling.right)){ //空节点也是black
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if(parentBlack){ //父节点为黑,下溢
afterRemove(parent, null);
}
}else{ //兄弟节点至上有一个red
if(isBlack(sibling.right)){ //左边如果是Black,则为LR,则转换成LL的情况
rotateRight(sibling);
sibling = parent.right;
}
color(sibling,colorOf(parent));
black(parent);
black(sibling.right);
rotateLeft(parent);
}
}else{ //被删除结点在右边,兄弟节点在左边
if(isRed(sibling)){ //兄弟节点是红色,将其转换成兄弟节点是黑色的情况
black(sibling);
red(parent);
rotateRight(parent);
sibling = parent.left;
}
//兄弟节点是黑色
if(isBlack(sibling.left) && isBlack(sibling.right)){ //空节点也是black
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if(parentBlack){ //父节点为黑,下溢
afterRemove(parent, null);
}
}else{ //兄弟节点至上有一个red
if(isBlack(sibling.left)){ //左边如果是Black,则为LR,则转换成LL的情况
rotateLeft(sibling);
sibling = parent.left;
}
color(sibling,colorOf(parent));
black(parent);
black(sibling.left);
rotateRight(parent);
}
}
}
原文:https://www.cnblogs.com/csluoyao/p/13061101.html