总目录 > 8 图论 > 8.5 最短路
前言
图论基础算法中最经典的问题!因为实在是太常见了,适用于不同情况的算法也很多。
当时对知识框架并没有概念的时候,对最短路的算法还是挺记忆犹新的,Floyd 和 Dijkstra 的双排故事还在继续。
子目录列表
1、最短路径
2、Floyd 算法
3、Dijkstra 算法
4、Bellman-Foed算法(施工中)
5、SPFA 算法(施工中)
6、Johnson 算法(施工中)
8.5 最短路
1、最短路径
家住信阳的小 k 和小 q 想去贵阳玩耍,因为奇妙的原因,他们只能步行过去,现在手里有一张地图,只能沿着地图上的路径走,不考虑其他因素,他们想知道怎么走能最快到达贵阳?
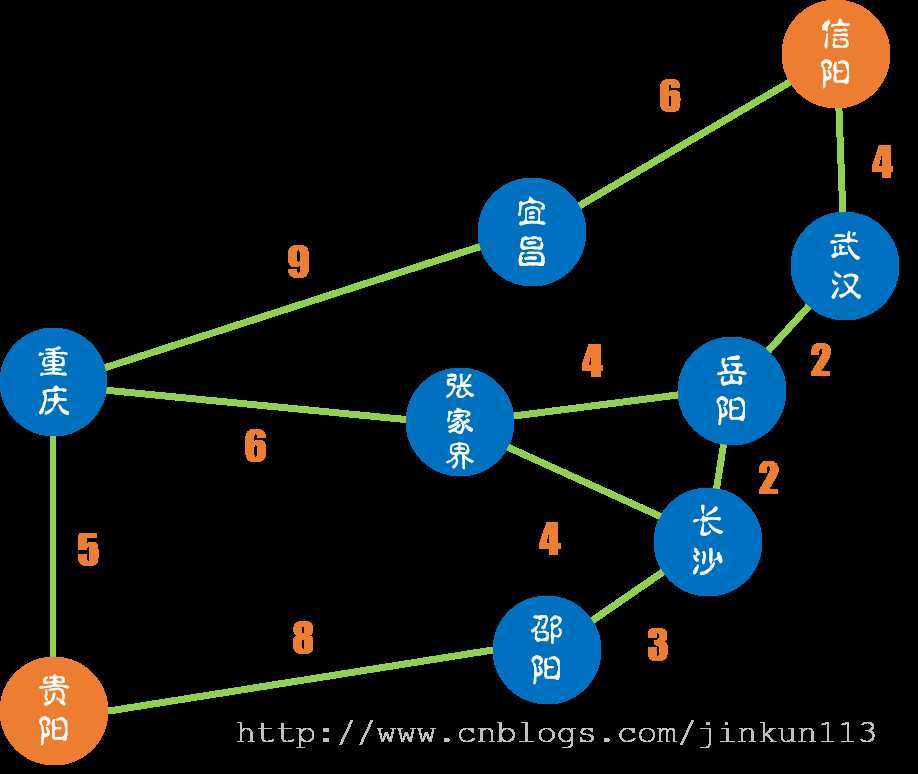
当然这是一张简化了许多的地图。通过手算,我们发现 “信阳 -> 武汉 -> 岳阳 -> 长沙 -> 邵阳 -> 贵阳” 这条路是最短的,距离为 19,也就是时间花费最少的。
如果地图变得庞大,我们就要采用各种手段来求了!
2、Floyd 算法
① 历史
Robert Floyd 老先生在 1962 年提出的这个算法。
② 核心思想
初始默认 n 个结点只能通过直接相连的边到达,即假设结点 x 和 结点 y 之间有一条边权为 w 的边,则它们的最短路为 w;如果直接没有边,则它们不可达。每次对其中一个结点 i 进行分析,
③ 实现
Floyd 算法本质上是一种动态规划。所以,我们用动态规划的框架来分析:
定义一个数组 f[i][j][k],表示只允许经过编号在 [1, i] 范围内的结点时,结点 j 到结点 k 的最短路长度。显然,f[n][j][k] 即结点 j 到结点 k 的最短路长度。
④ 优点
> 适用于任何图,有向无向,正权负权,只要最短路存在(即不存在负环),均可以使用;
> 很好理解,实现相当简单,三个 for 循环即可。
⑤ 缺点
> 复杂度极差,时间复杂度高达 O(n ^ 3),空间复杂度也不甘示弱 O(n ^ 2)。大多数情况下是不满足题目需求的。
⑥ 特点
将所有结点的任意两个结点之间的最短路同时求出,是一种多源最短路算法。适用于需要求出多对起点与终点的情况。
⑦ 代码
3、Dijkstra 算法
4、Bellman-Foed算法(施工中)
5、SPFA 算法(施工中)
6、Johnson 算法(施工中)
原文:https://www.cnblogs.com/jinkun113/p/13063162.html