地址 https://leetcode-cn.com/problems/regular-expression-matching/
作为算法问题实战策略 WILDCARD 的拓展 把leetcode的这题也解决掉了
这题是leetcode开头的第一道新人劝退题
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.‘ 和 ‘*‘ 的正则表达式匹配。 ‘.‘ 匹配任意单个字符 ‘*‘ 匹配零个或多个前面的那一个元素 所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。 说明: s 可能为空,且只包含从 a-z 的小写字母。 p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。 示例 1: 输入: s = "aa" p = "a" 输出: false 解释: "a" 无法匹配 "aa" 整个字符串。 示例 2: 输入: s = "aa" p = "a*" 输出: true 解释: 因为 ‘*‘ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a‘。因此,字符串 "aa" 可被视为 ‘a‘ 重复了一次。 示例 3: 输入: s = "ab" p = ".*" 输出: true 解释: ".*" 表示可匹配零个或多个(‘*‘)任意字符(‘.‘)。 示例 4: 输入: s = "aab" p = "c*a*b" 输出: true 解释: 因为 ‘*‘ 表示零个或多个,这里 ‘c‘ 为 0 个, ‘a‘ 被重复一次。因此可以匹配字符串 "aab"。 示例 5: 输入: s = "mississippi" p = "mis*is*p*." 输出: false
解答
问题的是确认*作为替代字符 会提到什么字符会替代几次
暴力遍历可以模拟* 提到0次到n次的各种尝试 然后递归求解。显然时间和空间的压力很大
所以我们可以采用动态规划
dp[i][j] 表示 字符串p 1~i的字符子串能成功匹配 字符串s1~j的字符子串
dp[i][j]能否成功匹配 取决于dp[i]-1[j-1]是否匹配成功 且 p[i]是否等于s[j].当然 如果p[i]==‘.‘ 就肯定等于s[j]
p[i]==‘*‘的情况就需要考虑*重复0到n次的情况,由于动规是逐层递进,且成功匹配具有传递性。
也就是dp[i][j] = dp[i][j-1]=dp[i][j-2]....... 一旦任意一个dp[i][j-x]=1 dp[i][j]就=1
所以状态方程只需要解决 ‘*‘代替重复字母为0次和1次的情况就可以解决‘*‘重复0到n次的情况
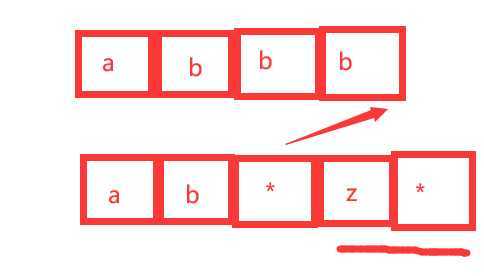
1 假设 p[i] == ‘*‘ 在‘*‘重复0次的情况下 dp[i][j] = dp[i-2][j];
如图 p字符串 z* 重复了0次 整个字符串相等与否 取决于 s[1~j] 与 p[1~(i-2)] 是否匹配
2 假设p[i] == ‘*‘ 重复1次dp[i][j] = dp[i-2][j-1]
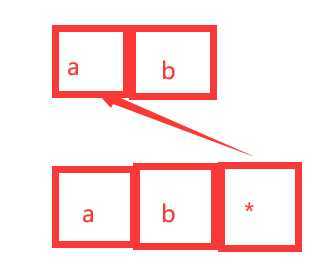
如图 p字符串中 b*重复1次是否匹配取决于b*重复0次的情况
代码如下
考虑到字符串是以0开始 dp还需要考虑空字符串的比较 那么最好添加一层空层 处理就可以从索引1开始 比较便于调试和理解
class Solution { public: int dp[1100][1100]; bool isMatch(string s, string p) { s = " " + s; p = " " + p; dp[0][0] = 1; for (int i = 1; i < p.size(); i++) { if (p[i] == ‘*‘) dp[i][0] = dp[i-2][0]; for (int j = 1; j < s.size(); j++) { if (p[i] == ‘.‘) { dp[i][j] = dp[i - 1][j - 1]; } else if (p[i] == s[j]) { dp[i][j] = dp[i - 1][j - 1]; }else if (p[i] == ‘*‘) { dp[i][j] |= dp[i-2][j]; if(p[i-1] == ‘.‘ || p[i-1] == s[j]) dp[i][j] |= dp[i][j-1]; } } } return dp[p.size()-1][s.size()-1]; } };
原文:https://www.cnblogs.com/itdef/p/13069736.html