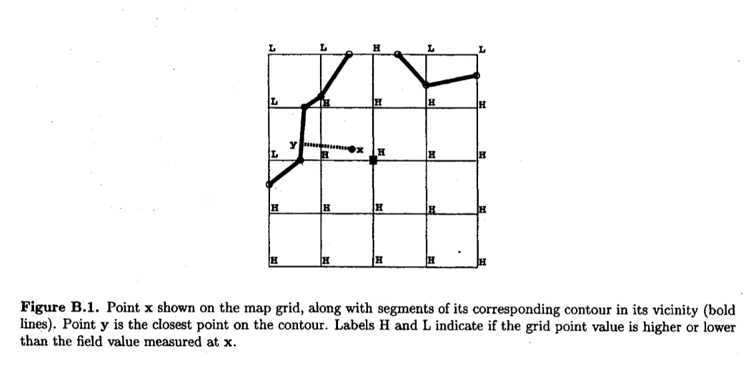
在ICCP算法当中,从高度/重力地图中提取等值线是重要步骤。1999年的文章《Vehicle localization on gravity maps》中详细地介绍了ICCP算法每一个步骤的实现方法。
其中,提取等值线部分的算法叙述如下:

大致过程是搜索规定区域内每个网格点的四条边,判断等值线是否经过其中两条边。若水深/重力等值线f值在某条边的两个端点的值之间,则认为等值线经过该条边。
假设等值线与一条横边相交,等值线与该条边的交点横坐标为:

纵坐标与该条边的网格点相同。
根据该论文中给出的例子,设计网格点坐标和坐标对应的水深/重力值。假设需要提取的等值线值为f=2。
MATLAB代码如下:
clc; clear all; xx=[0,1,2,3,4]; yy=[4;3;2;1;0]; for i=1:5 xx(i,:)=[0,1,2,3,4]; end for i=1:5 yy(:,i)=[4;3;2;1;0]; end zz1=[3,0,4; 4,0,0; 0,0,0]; z=[0,0,5,0,0; 0,3,5,4,4; 0,4,5,5,5; 5,5,5,5,5; 5,5,5,5,5]; %创建网格点坐标及重力值 k=1; f=2; %待提取等值线值 flag=1; %需要扩大搜索区域 if f>max(zz1) flag=0; end if f<min(zz1) flag=0; end if flag for i=1:5 %搜索网格点 for j=1:5 if z(i,j)==f contour(k,1)=xx(i,j); contour(k,2)=yy(i,j); k=k+1; end end end for i=1:4 for j=1:4 if (f>z(i,j) && f<z(i,j+1)) || (f>z(i,j+1) && f<z(i,j)) %网格单元上边 contour(k,1)=xx(i,j)+(f-z(i,j))/(z(i,j+1)-z(i,j))*(xx(i,j+1)-xx(i,j)); contour(k,2)=yy(i,j); k=k+1; end if (f>z(i+1,j) && f<z(i+1,j+1)) || (f>z(i+1,j+1) && f<z(i+1,j)) %网格单元下边 contour(k,1)=xx(i+1,j)+(f-z(i+1,j))/(z(i+1,j+1)-z(i+1,j))*(xx(i+1,j+1)-xx(i+1,j)); contour(k,2)=yy(i+1,j); k=k+1; end if (f>z(i,j) && f<z(i+1,j)) || (f>z(i+1,j) && f<z(i,j)) %网格左边 contour(k,1)=xx(i,j); contour(k,2)=yy(i,j)+(f-z(i,j))/(z(i+1,j)-z(i,j))*(yy(i+1,j)-yy(i,j)); k=k+1; end if (f>z(i,j+1) && f<z(i+1,j+1)) || (f>z(i+1,j+1) && f<z(i,j+1)) %网格右边 contour(k,1)=xx(i,j+1); contour(k,2)=yy(i,j+1)+(f-z(i,j+1))/(z(i+1,j+1)-z(i,j+1))*(yy(i+1,j+1)-yy(i,j+1)); k=k+1; end end end end %画图 plot(xx(:),yy(:),‘k.‘); grid on; hold on; for i=1:2:11 plot(contour(i:i+1,1),contour(i:i+1,2),‘r-‘); hold on; end
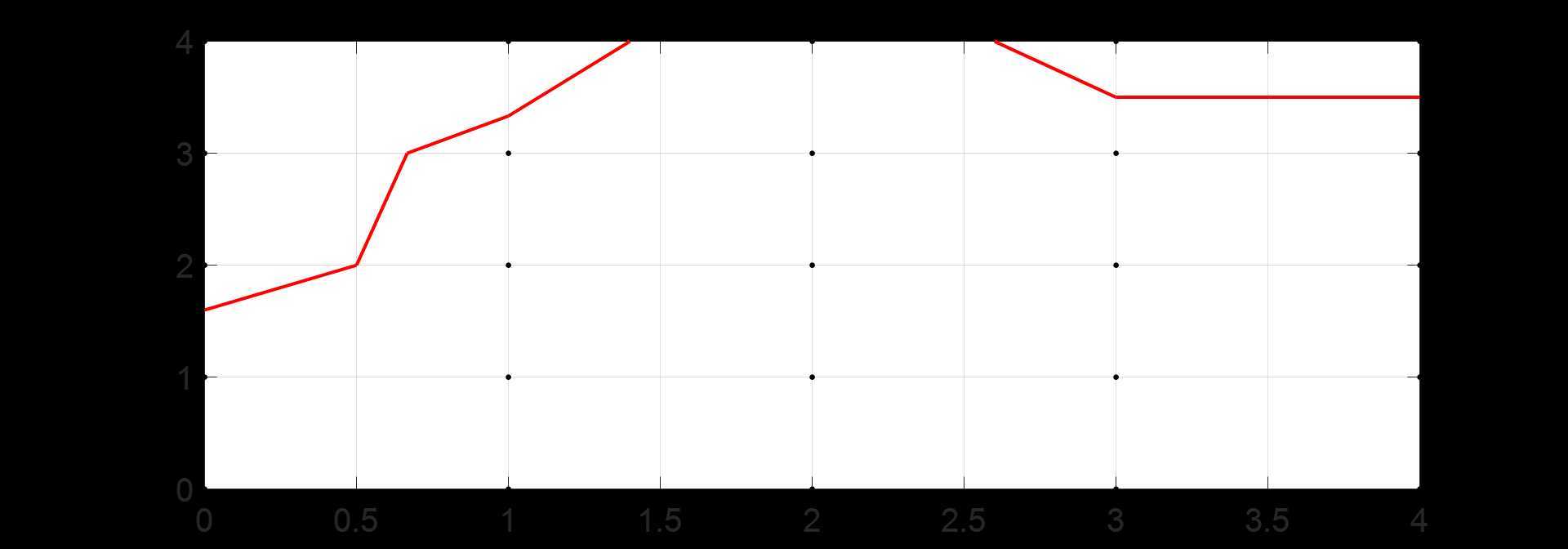
需要注意的是,储存经过网格单元等值线线段的两个端点,便于后续寻找等值线上最近点。在网格单元内不对水深/重力值进行插值。
得到的提取等值线(红色)结果如下:
原文:https://www.cnblogs.com/huangliu1111/p/13089188.html