A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:
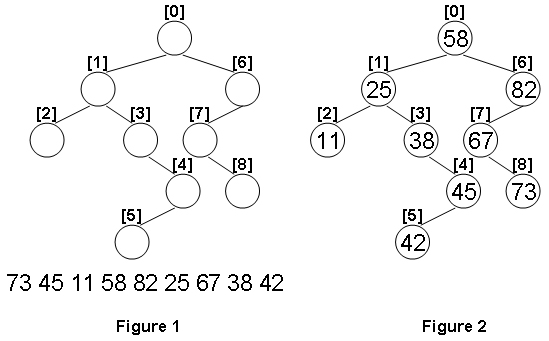
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.
Each input file contains one test case. For each case, the first line gives a positive integer N (≤) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then − will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.
For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.
9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42
58 25 82 11 38 67 45 73 42
这题我一开始的思路是先按照给出的节点数据层序遍历建树,这次建树是为了固定BST每个节点的位置。由于BST的中序遍历就是
元素值的排序,因此我们将读入的值排序,然后中序遍历之前固定位置用的那棵树,再将值一一插入。最后层序输出。
层序遍历的代码上面有个需要注意的地方。如果你要将一个节点加入队列,那你必将先为这个节点开辟空间再将其加入,坚决不
能先加入队列,然后再分配空间。
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <queue> 5 using namespace std; 6 7 struct Tree { 8 int data; 9 Tree *l, *r; 10 } *root; 11 typedef Tree* ptree; 12 13 int n, lc, rc; 14 15 vector <int> ans; 16 17 typedef pair <int, int> pii; 18 19 pii vec[100 + 5]; 20 21 void level(ptree &root) { 22 queue <ptree> que; 23 root = new Tree; 24 root -> data = 0; 25 root -> l = root -> r = NULL; 26 que.push(root); 27 while(!que.empty()) { 28 ptree now = que.front(), temp; 29 int k = now -> data; 30 que.pop(); 31 lc = vec[k].first, rc = vec[k].second; 32 if(~lc) { 33 temp = new Tree; 34 temp -> data = lc; 35 temp -> l = temp -> r = NULL; 36 now -> l = temp; 37 que.push(temp); 38 } 39 if(~rc) { 40 temp = new Tree; 41 temp -> data = rc; 42 temp -> l = temp -> r = NULL; 43 now -> r = temp; 44 que.push(temp); 45 } 46 } 47 } 48 49 int val[100 + 5]; 50 51 int cnt; 52 53 void inorder(ptree &root) { 54 if(root == NULL) { 55 return; 56 } 57 inorder(root -> l); 58 root -> data = val[cnt ++]; 59 inorder(root -> r); 60 } 61 62 void levelorder(ptree root) { 63 if(root == NULL) return; 64 queue <ptree> que; 65 que.push(root); 66 while(!que.empty()) { 67 ptree now = que.front(); 68 que.pop(); 69 ans.push_back(now -> data); 70 if(now -> l) que.push(now -> l); 71 if(now -> r) que.push(now -> r); 72 } 73 } 74 75 int main() { 76 scanf("%d", &n); 77 for(int i = 0; i < n; i ++) { 78 scanf("%d %d", &lc, &rc); 79 vec[i] = make_pair(lc, rc); 80 } 81 level(root); 82 for(int i = 0; i < n; i ++) { 83 scanf("%d", &val[i]); 84 } 85 sort(val, val + n); 86 inorder(root); 87 levelorder(root); 88 for(int i = 0; i < ans.size(); i ++) { 89 if(i) printf(" "); 90 printf("%d", ans[i]); 91 } 92 printf("\n"); 93 return 0; 94 }
是的,上面的是我这种蠢人的做法。。。
AC了之后看到别人直接中序遍历建树,我吐了。
为什么是直接中序遍历建树呢?
我们一开始读入了从0 ~ n所有节点的左右儿子的idx。
然后如果我们用刚刚读入的数据从idx[0]直接开始中序遍历建树,因为如果中序遍历建树,那么我们就可以直接在访问到一个节点的
时候把值赋给他。因此并不需要先层序遍历确定树的结构,因为你中序建树用的也是这些节点,你建的树模子和层序建的树一模一样
,因此你只需要在中序建树的时候顺便把相应的值赋给他就ok了。代码就不实现了吧。直接递归建,数据小。1099 Build A Binary Search Tree (30分)(BST的层序或者中序遍历建树,层序便利输出树)
原文:https://www.cnblogs.com/bianjunting/p/13096611.html