以猜数字游戏引出的分治算法的理解与思考

一、背景

分治算法是计算机五大常用算法之一，也是在JAVA编程中经常用到的算法之一。对于分治算法的理解，往往会停留在一些枯燥的概念上，比如“分而治之”，“问题原子分解”等。该文将会通过一个猜数字的游戏入手，引出对于分治算法基本思想的思考。

二、猜数字游戏

2.1 游戏规则

• 由电脑生成一个在【1-100】之间的随机整数；
• 人类每轮只能猜测一个数字；
• 电脑根据人类给出的数字进行反馈：
  -- 人类给出的数字比电脑给出的数字大，则反馈“比这个数字要大”；
  -- 人类给出的数字比电脑给出的数字小，则反馈“比这个数字要小”；
  -- 人类给出的数字等同于电脑给出的数字，则反馈“猜中了”。
• 不限猜数轮次，以猜中为准

2.2 猜数字游戏源码

• 根据游戏规则，我们先形成编码：

/**
 * 猜数字游戏
 *
 * @author zhuhuix
 * @date 2020-06-11
 */
public class Guess {

    public static void main(String[] args) throws IOException {
        int num = generateRandomInteger(1, 100);
        int guessNum = 0;
        BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
        System.out.println("已生成一个【1-100】的整数，请开始猜数...");
        while (num != guessNum) {

            String s = bufferedReader.readLine();
            if (!s.matches("[0-9]+")) {
                System.out.println("请输入一个整数..");
                continue;
            }
            guessNum=Integer.parseInt(s);
            if (guessNum > 100 || guessNum < 1) {
                System.out.println("请输入一个【1-100】整数..");
                continue;
            }
            if (guessNum<num){
                System.out.println("Sorry,比这个数字要大，请继续...");
            }
            if (guessNum>num){
                System.out.println("Sorry,比这个数字要小，请继续...");
            }

        }

        System.out.println("恭喜您猜中了!!!");

    }

    /**
     * 产生一个在规定范围内的随机数
     *
     * @param left  起始数字
     * @param right 终止数字
     * @return 随机数
     */
    private static int generateRandomInteger(int left, int right) {
        Random random = new Random();
        return left + random.nextInt(right - left + 1);
    }
}

2.3 猜数字游戏技巧

• 看看人类是怎么猜的：
  --有没有发现规律？
  
• 人类猜数字的技巧：
  -- 先猜50这个中位数，
  -- 根据电脑“大”或“小”的反馈将数字范围对半拆分
  --循环重复以上分解过程，直至找到对应的数字为止
  

三、分治算法

3.1 思想与策略

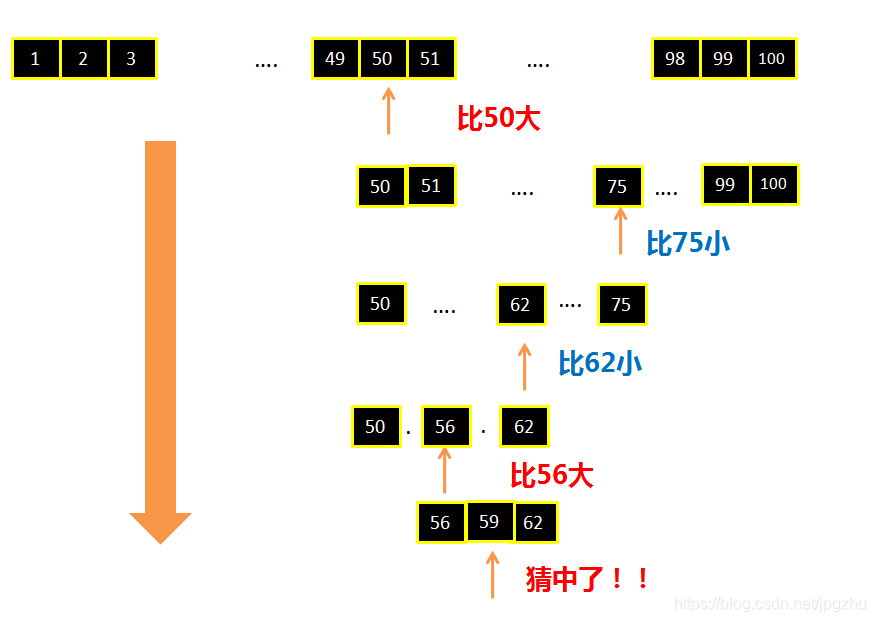
将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

• 注意：是相同问题，就象猜数字游戏一样，原来的问题是【1-100】的数，分割成的是【1-49】，【50-100】，【50-75】...这些缩小了规模的数，问题的性质始终没变。

3.2 适用的特征

• 问题缩小到一定规模就容易解决：比如猜数字游戏数字范围从【1-100】缩小到【56-62】，就容易猜中。
• 问题缩小规模后形成的子问题是相互独立的。
• 问题规模不管怎么缩小，性质不能改变。
• 利用该问题分解出的子问题的解可以合并为该问题的解

3.3 分治算法的典型应用

3.3.1 归并排序的原理

归并排序就是一种典型的分治算法：将N个数字的一个大规模表分成1个数字的N个小规模表，再通过数字从小到大的顺序从1个数字的N个小规模表合并成N个数字的一个大规模表

3.3.2 自顶向下的归并排序源码

/**
 * 整型数组排序统一接口定义
 *
 * @author zhuhuix
 * @date 2020-06-06
 */
public interface Sort  <T extends Comparable<? super T>> {

    /**
     * 整型排序
     * @param arr 待排序数组
     */
   void sort(T[] arr);
}

/**
 * 归并排序
 *
 * @author zhuhuix
 * @date 2020-06-11
 */
public class MergeSort<T extends Comparable<? super T>> implements Sort<T> {
    @Override
    public  void sort(T[] arr) {
        mergeSort(arr,0,arr.length-1);
    }

    private void mergeSort(T[]arr,int l,int r){
    	// 递归退出条件：分到最小规模为止
        if (r-l<=0){
            return;
        }
        // 取到当前规模的中值
        int mid = (l+r)/2;
       // 中值的左边递归分解
        mergeSort(arr,l,mid);
        // 中值的右边递归分解
        mergeSort(arr,mid+1,r);
        // 排序合并
       if (arr[mid].compareTo(arr[mid + 1]) > 0) {
            merge(arr, l, mid, r);
        }
    }

    private void merge(T[]arr,int l,int mid,int r){
        T[]aux=Arrays.copyOf(arr,r-l+1);
        for (int i = l; i <= r; i++) {
            aux[i - l] = arr[i];
        }
        int i = l, j = mid + 1;
        for (int k = l; k <= r; k++) {

            if (i > mid) {
                arr[k] = aux[j - l];
                j++;
            } else if (j > r) {
                arr[k] = aux[i - l];
                i++;
            } else if (aux[i - l].compareTo(  aux[j - l])<0) {
                arr[k] = aux[i - l];
                i++;
            } else {
                arr[k] = aux[j - l];
                j++;
            }
        }
    }

 }

四、总结

1. 分治算法的难点就是”如何分“：每个分解出来的子问题需独立存在；比如整数数组排序时需要从N个数分到1个数...
2. 分治算法一般会涉及递归程序；
3. 分治算法在从小规模问题合并成大规模问题的过程中，一般需要开辟辅助空间处理。

以猜数字游戏引出的分治算法的理解与思考

原文：https://www.cnblogs.com/zhuhuix/p/13098682.html