Educational Codeforces Round 89 (Rated for Div. 2) C. Palindromic Paths (思维)

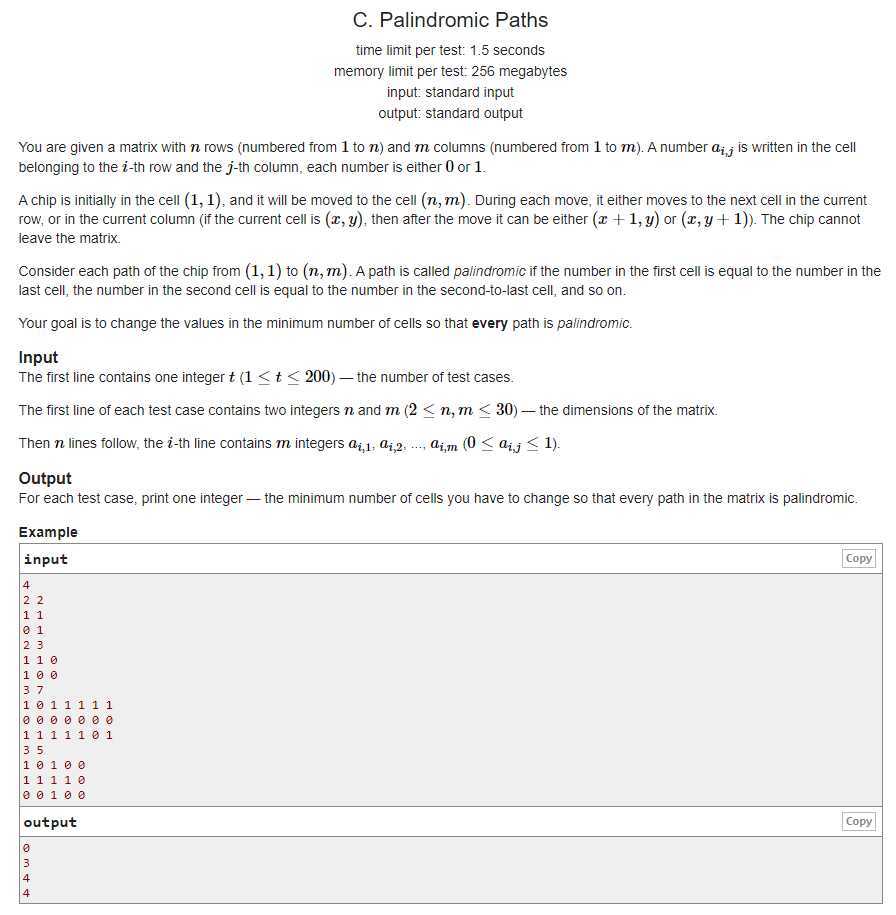
• 题意:有一个\(n\)x\(m\)的矩阵,从\((1,1)\)出发走到\((n,m)\),问最少修改多少个数,使得所有路径上的数对应相等(e.g:\((1,2)\)和\((n-1,m)\)或\((2,1)\)和\((n,m-1)\)).

• 题解:我们将二维的点的坐标转化为一维的步数(到\((1,1)\)的路径),统计所有步数相同的数字,然后枚举步数及相对应位置的数字,这些位置上的所有数字都应该相等,所以取一个\(0\)和\(1\)出现次数的最小值即可.

• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  
  int t;
  int n,m;
  int dis[N][2];
  int a[100][100];
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
  	cin>>t;
  	 while(t--){
  	 	cin>>n>>m;
  	 	me(dis,0,sizeof(dis));
  	 	for(int i=1;i<=n;++i){
  	 		for(int j=1;j<=m;++j){
  	 			cin>>a[i][j];          //step=n+m-2;
  	 			int step=i+j-2;
  	 			dis[step][a[i][j]]++;
  	 		}
  	 	}
  	 	int sum=n+m-2;
  	 	int ans=0;
  	 	for(int i=0,j=sum;i<j;++i,--j){
  	 		ans+=min(dis[i][0]+dis[j][0],dis[i][1]+dis[j][1]);
  	 	}
  	 	printf("%d\n",ans);
  	 	
  	 }
  
      return 0;
  }
  

Educational Codeforces Round 89 (Rated for Div. 2) C. Palindromic Paths (思维)

原文：https://www.cnblogs.com/lr599909928/p/13110312.html