【核心算法3】深度优先遍历算法

深度优先遍历算法是经典的图论算法，深度优先遍历算法的搜索逻辑跟它名字一样，只要有可能，就尽量深入搜索，知道找到答案，或者尝试了所有可能后确定没有解。

• 什么是深度优先遍历
• 二叉树
• 怎么抓住小偷
• 二叉树中的最大路径和
• 最大的岛屿

什么是深度优先遍历

沿着一个目的不断的检索，直到把所有的问题都解决，再去检索下一个目的。

检索问题的本质就是试探问题的所有可能性，按照特定的规律和顺序，不断地去搜索答案，直到找到问题的解。若把所有可能都走一遍，也没找到解，就说明这个问题没有解。

二叉树

二叉树是一种特殊的数据结构。常见的数据结构包含数组、链表、图、队列、散列表与树。

二叉树的每一个节点都有两个分支，称为“左子树” 与 “右子树”。二叉树的每一层最多有（2^n - 1）个节点

二叉树的类型

• 空二叉树: 有零个节点
• 满二叉树: 每一个节点都有零个或者两个子节点
• 完全二叉树: 除了最后一层，每一层的节点都是满的，并且最后一层的节点全部从左排序
• 完美二叉树: 每一层的节点都是满的
• 平衡二叉树: 每个节点的两个子树的深度相差不超过1

二叉树的相关术语

二叉树的节点代码

因为每一个节点都与两个子节点相连，所以只需要拥有根节点就能找到二叉树任意节点。

class Node():
    
    def __init__(self, x):
        # 节点值
        self.val = x
        # 左侧节点
        self.left = None
        # 右侧节点
        self.right = None

二叉树的遍历顺序

L、R、D分别代表左子树、右子树和根

• DLR(先序)：先遍历根，再遍历左子树，最后遍历右子树
• LDR(中序)：先遍历左子树，再遍历根，最后遍历右子树
• LRD(后序)：先遍历左子树，再遍历右子树，最后遍历根

如图：

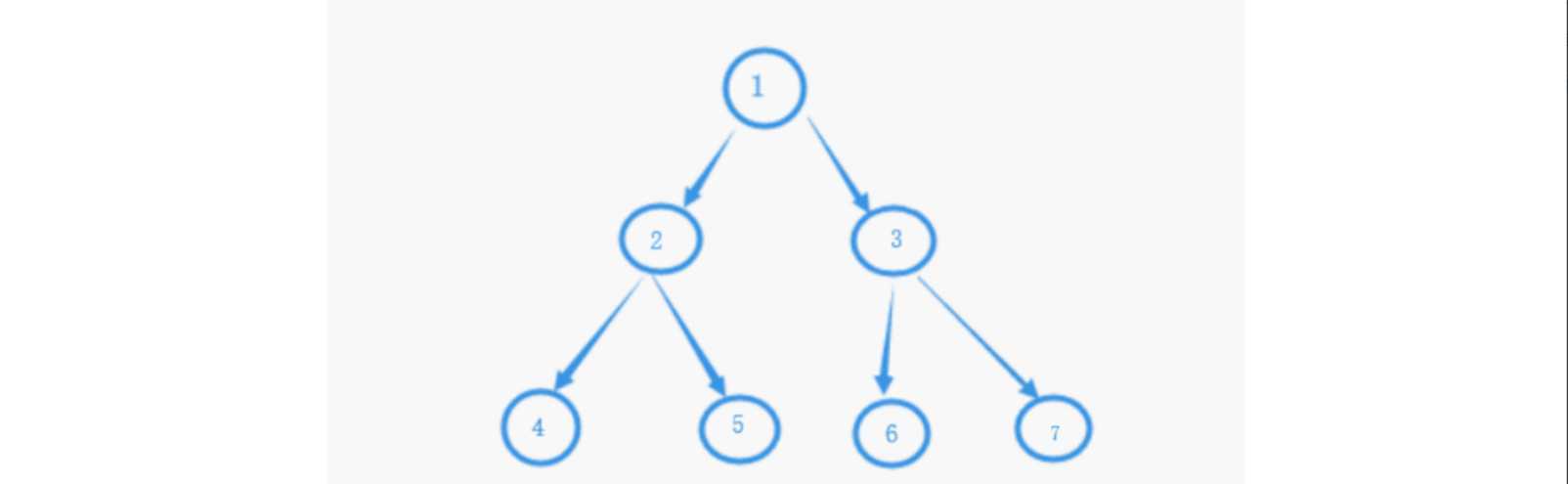
节点的访问顺序

- DLR(先序)： 1-2-4-5-3-6-7
- LDR(中序)： 4-2-5-1-6-3-7
- LRD(后序)： 4-5-2-6-7-3-1

深度遍历与广度遍历

从先序，中序，后序年里都属于深度优先遍历。在深度优先遍历中，从根节点出发直奔最远的节点。而在广度优先遍历中，首先访问离根节点最近的节点，按层递进。以上图为例，顺序为：1-2-3-4-5-6-7.

【核心算法3】深度优先遍历算法

原文：https://www.cnblogs.com/JoshuaP/p/13089403.html