进度日志

• 公共课一：政治
• 公共课二：英语一
• 业务课一：数学一
• 业务课二：自动控制原理、信号与系统

20200612

• 昨晚12点过睡的，早上五点二十八醒了。下场就是十一点到十二点间趴在桌上口水流在了一阶微分方程那一面的夹缝中...
• 好吧，上午看了一节常微分方程的视频，但好像对复习没什么帮助，讲的是欧拉数值法求微分方程的近似解曲线，数值计算方向，想起之前的编程课。好吧，真得实际一点。
• 下午，纠结着要不要从数学模型传递函数开始，但，纠结了一会儿。打算从时域分析开始啃起。于是：稳定性分析、动态静态性能指标、劳斯判据。
• 晚上，结束了劳斯判据的学习，稳定性分析算是结束了。但是还有习题没有做，微分方程也没有做习题，感觉有点慌张。13号...按琢磨着该看看概率了。概率，看参数估计？算了，还是线性代数吧。

公共课一

NONE

公共课二

无

业务课一

• 微分方程-视频
  • 欧拉数值法
    • 步长e决定误差h
      • e~ch
    • 选择更好的斜率，牺牲计算速度来得到更高的精度
      • RK4常用
    • 数值计算法的难点
      • 不连续（奇点）的不确定性，欧拉步骤失效
• 代数
  • 多项式除法、长除法、综合除法
    • 长除法的特殊简化版->综合除法
      • 综合除法(x-a)，是一种简化写法
      • 嗯...我还是老老实实用长除法吧

业务课二

• 经典控制理论-视频
  • 时域分析法
    • 稳定性分析
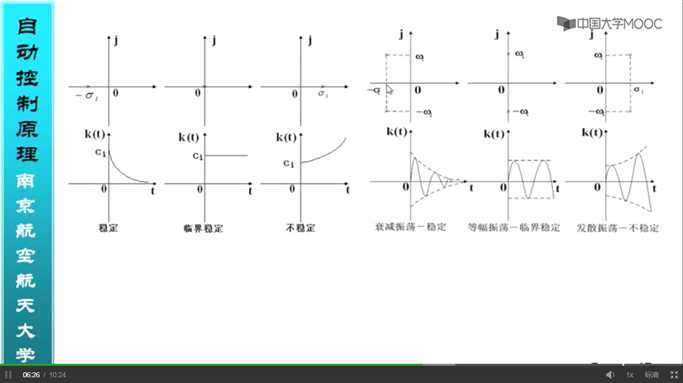
      • 稳定系统的单位阶跃响应一定收敛
      • 不稳定系统的单位阶跃响应一定发散或者等幅振荡，无需研究其时域性能
      • 系统稳定性的定义
        • 若系统在初始偏差作用下，随时间的推移，偏差逐渐衰减并趋于零，即系统具有恢复原平衡状态的能力，则称系统渐进稳定，简称稳定。
        • 初始偏差、外界扰动、初始状态响应
      • 系统初始状态响应的拉氏变换与系统闭环传递函数具有相同的形式且分母多项式相同，仅分子多项式系数不同。
        • 系统的单位脉冲响应实际为系统闭环传递函数的拉普拉斯反变换
        • 系统初始状态响应与系统单位脉冲响应具有相同的形式，即各极点对应的衰减“基”相同，不同的仅为各个响应分量的系数不同。
        • 故，初始偏差响应衰减并趋于零等同于，在时间趋于无穷时，系统的单位脉冲响应趋于零。
      • Q：为什么极点存在虚部便会振荡？虚部与振荡.
      • 系统稳定：即闭环特征方程的根均有负实部。
        • 系统不稳定：根位于s右半平面，含虚轴。
        • 系统临界稳定：存在根位于虚轴，但其余均有负实部。(严格意义上讲，临界稳定不稳定)
    • 劳斯稳定判据
      • 对高阶系统来说，求出闭环特征方程的根是不容易的->劳斯
      • 系统稳定的必要条件：特征方程的所有系数均为正，且不缺项。
        • 系数中有负数或零（缺项），则系统一定不稳定。而满足必要条件，系统并不一定稳定。
      • 系统稳定的劳斯判据
        • 系统稳定的充分必要条件是劳斯表的第一列元素均为正。
        • 若第一列元素出现负值，系统不稳定。
        • 且若出现负值，则第一列元素符号改变的次数等于特征方程正实部根的数量。（注意，并不能判断虚轴上的根的情况，即第一列元素变号次数并不含位于s平面虚轴上的根。）
          • ? 若第一列元素全为负值呢？改变次数为零，说明...
            • 说明个鬼，不稳定了，没法用劳斯判据判断正实部根的数量
              • 屁！不稳定不能判断正实部根的数量？脑子秀逗了？劳斯稳定判据看仔细点!
              • 好吧，是对应方程至少有一个根不在复左半平面？为什么？？这正确么？
        • 劳斯稳定判据的特殊情况
          • a. 某行的第一列元素为零，其他元素不为零或不全为零。->处理方法
            • 用正无穷小量\epsilon来代替零，继续列写并完成劳斯表，按照结果进行判定。
          • b. 某一行的元素全为零（全零行）-> 处理方法
            • 1> 利用全零行上一行元素构造辅助方程F(s)=0
            • 2> 对辅助方程求导，将求导所得的系数代替全零行，继续列写劳斯表，但注意，此时列写完毕后不能得出系统稳定与否，需要对辅助方程进行求解判断根的情况。
            • 3> 我们可以通过解辅助方程来观察究竟是什么原因使得劳斯表全零行的出现，即根是怎么样的一个特殊情况。
              • 出现全零行，就一定存在关于s平面虚轴对称的特征根。（此时要注意虚轴上的根所对应的不稳定性（临界稳定也归属为不稳定））
              • 劳斯表出现全零行，有根位于虚轴上。
            • 注意在该情况下用综合除法得到的商（长除法也行）求出剩下的根。
        • 若系统特征方程系数存在非正根，虽然可直接得出系统不稳定，但仍可以通过列写劳斯表来得出待定系统闭环极点的分布（有多少个极点在右半平面（不包括虚轴））
        • 劳斯判据的应用
          • 确定使系统稳定的参数变化范围
          • 检验系统的稳定程度
            • s=s-σ
        • 劳斯表第一列元素的变号次数不含虚轴上的根
        • 出现全零行，不能仅由变号次数判定稳定性。
        • 关于虚轴对称的根包括位于原点、虚轴上的根。可通过解辅助方程求得。
        • 按照劳斯表的计算规则，每行元素可以同乘一个相同的正数，不影响其元素符号，也不影响判定。
        • 为简化计算，若上一行第一列元素为确定值，则进行计算时只需根据其上一行第一列元素的正负，乘以+1或者-1
          

• 非第一种劳斯判据的特殊情况，即出现第一列元素为零；此处实为第二种劳斯判据的特殊情况，即出现全零行。->涉及到计算s^0行的补零
  

20200612-

原文：https://www.cnblogs.com/shuuei/p/13098963.html