机器学习笔记(3)-最小二乘法
最小二乘法(又称最小平方法),它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
一个非常直观的例子,假设图中有一些点,我们通过一条直线去拟合,那么所有点(观测数据)到直线的距离(y的差值)的差的平方和就是我们要的东西,这个东西我们又可以称为关于这条直线的参数\(w\)的损失函数。
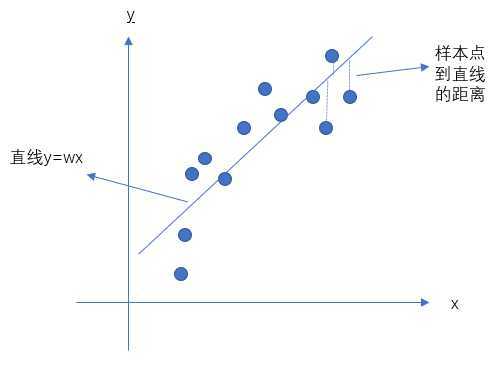
最小二乘估计
假设我们有n个数据样本点,\(D={(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})}\)
\(Y=W^TX\),这里为了方便,令\(b=w_{1}x_{1},x_{1}=1\),其中:
- \(x_{i}\in \mathbb{R}^{p},y_{i}\in\mathbb{R}\);
- \(X=(x_{1},x_{2},...,x_{n})^T_{n*p}, Y=(y_{1},y_{2},...,y_{n})^T_{n*1}\);
- \(W=(w_{1},w_{2},...,w_{n})^T_{p*1}\)
于是我们得到关于\(L(W)\)的损失函数:
\[\begin{aligned}
L(W)&=\sum_{i=1}^{n}\left \| W^Tx_{i}-y_{i} \right \|^2\&=\sum_{i=1}^{n}(W^Tx_{i}-y_{i})\cdot (W^Tx_{i}-y_{i})\&=\begin{pmatrix}
W^Tx_{1}-y_{1}& W^Tx_{2}-y_{2} & \cdots & W^Tx_{n}-y_{n}
\end{pmatrix}\cdot
\begin{pmatrix}
W^Tx_{1}-y_{1}\\
W^Tx_{2}-y_{2}\\
\vdots \\
W^Tx_{n}-y_{n}
\end{pmatrix}\&=(W^TX^T-Y^T)\cdot (W^TX-Y)\&=W^TX^TW^TX-W^TX^TY-Y^TW^TX+Y^TY
\end{aligned}
\]
观察上式结果,发现:
\(W^TX^TY=W^T_{1*p}X^T_{p*n}Y_{n*1}\)这个结果是一个1*1的标量,同理\(Y^TW^TX\)也是一个标量,所以它们相等,于是:
\[L(W)=W^TX^TW^TX-2W^TX^TY+Y^TY
\]
接下来,我们对上式采用取最小值,利用偏导为0得到最低值:
\[\begin{aligned}
L(W)&=\underset{w}{argmin}\;W^TX^TW^TX-2W^TX^TY+Y^TY\\frac{\partial L(W)}{\partial w}&=2X^TXW^T-2X^TY=0
\end{aligned}
\]
最后我们得到\(W\)的解析解:
\[\begin{aligned}
2X^TXW^T&=2X^TY\W^T&=(X^TX)^{-1}X^TY
\end{aligned}
\]
另一种几何解释
之前我们提到最小二乘法的几何解释就是所有点(观测数据)到直线的距离(y的差值)的差的平方和,其实我们还可以换一种角度来看,把\(X\)看成是p个n维空间的向量(每个\(x_{i}\)都对应不同的方向),而不是之前n个p维的向量
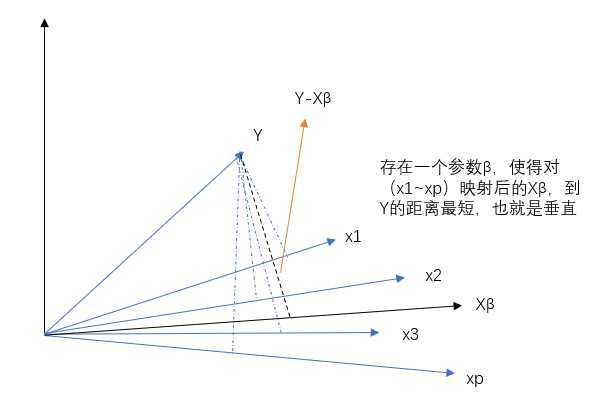
也就是说,我们要找到一个\(X\beta\)并且使\(Y\)到上面的距离最小(误差距离最低)即\(Y-X\beta\),而这个最小距离的直线方向和\(X\)中的每个\(x_{i}\)都是垂直的,所以点积为0:
\[\begin{aligned}
X^T(Y-X\beta)=0\X^TX\beta=X^TY\\beta=(X^TX)^{-1}X^TY
\end{aligned}
\]
可以看到结果和之前的解析解是一样的。
利用极大似然估计求解
上面介绍的是通过最小二乘法来求解参数\(W\),这节我们采用极大似然估计(MLE)来得到损失函数求解,看看结果是不是一样,在什么样的条件下一样。
我们假设有个噪声是服从正太分布的,即\(\epsilon \sim N(\mu,\sigma^2)\),这样在每一个样本上我们加上这个噪声,则可以得到:
- 假设存在噪声服从正态分布:\(\epsilon \sim N(\mu,\sigma^2)\)
- 每个数据点添加噪声:\(Y=W^TX+\epsilon\)
- 于是得到Y的分布:\(y_{i}\sim N(\mu+W^TX,\sigma^2)\)
- 进一步得到:\(P(Y|X;W)=\frac{1}{\sqrt{2\pi }\sigma}exp(-\frac{(y_{i}-\mu-W^TX)^2}{2\sigma^2})\)
于是我们根据似然函数估计得到:
\[\begin{aligned}
L(W)&=P(Y|X;W)\&=\sum_{i=1}^{n}log\;p(y_{i}|x_{i};W)\&=\sum_{i=1}^{n}log\;\frac{1}{\sqrt{2\pi }\sigma}exp(-\frac{(y_{i}-\mu-W^Tx_{i})^2}{2\sigma^2})\&=\sum_{i=1}^{n}(-log\sqrt{2\pi }-log\sigma-\frac{(y_{i}-\mu-W^Tx_{i})^2}{2\sigma^2})
\end{aligned}
\]
然后通过MLE得到:
\[\begin{aligned}
\hat{W}_{MLE}&=\underset{w}{argmax}\sum_{i=1}^{n}(-log\sqrt{2\pi }-log\sigma-\frac{(y_{i}-\mu-W^Tx_{i})^2}{2\sigma^2})\&=\underset{w}{argmin}\sum_{i=1}^{n}(log\sqrt{2\pi }+log\sigma+\frac{(y_{i}-\mu-W^Tx_{i})^2}{2\sigma^2})\&=\underset{w}{argmin}\sum_{i=1}^{n}(y_{i}-\mu-W^Tx_{i})^2
\end{aligned}
\]
到这里可以很清晰的看到,当\(\mu=0\)时,\(\hat{W}_{MLE}=\underset{w}{argmin}\sum_{i=1}^{n}\left \| W^Tx_{i}-y_{i} \right \|^2\),对比最小二乘估计两者完全一致。
总结
最小二乘估计也是一种通过最小化误差的平方和寻找数据的最佳函数匹配的方法。
当样本添加一个噪声\(\epsilon \sim N(0,\sigma^2)\)时,最小二乘估计和极大似然估计是等价的。
机器学习笔记(3)-最小二乘法
原文:https://www.cnblogs.com/Epir/p/13121482.html

