来一个O(nlogn)做法,跑得挺快。
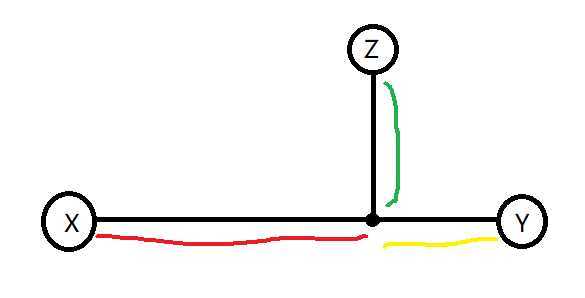
假设点集S包含点X,Y,Z,红色链长度为a,黄色链长度为b,绿色链长度为c。
如果|a-b|>1,那么有|dis(X,Z)-dis(Y,Z)|=|(a+c)-(b+c)|=|a-b|>1,不符合题目要求。
所以a=b或|a-b|=1。所以存在一个点A,到S中每一个点的距离都为p或p+1(0<2p<n),我们把这个距离p称为“点心距”。
接着发现一定是一下两种情况之一(证明留给读者自行思考):
情况1:S中任两点到点A的链没有公共边。
情况2:S中任意一点P满足min(dis(P,A),dis(P,A‘))=p(A‘为一个与A相邻的点)。
于是,S中的点便是由A点或者A点及A‘点伸出来的若干条“长度相近”链的另一端点组成(如图)。
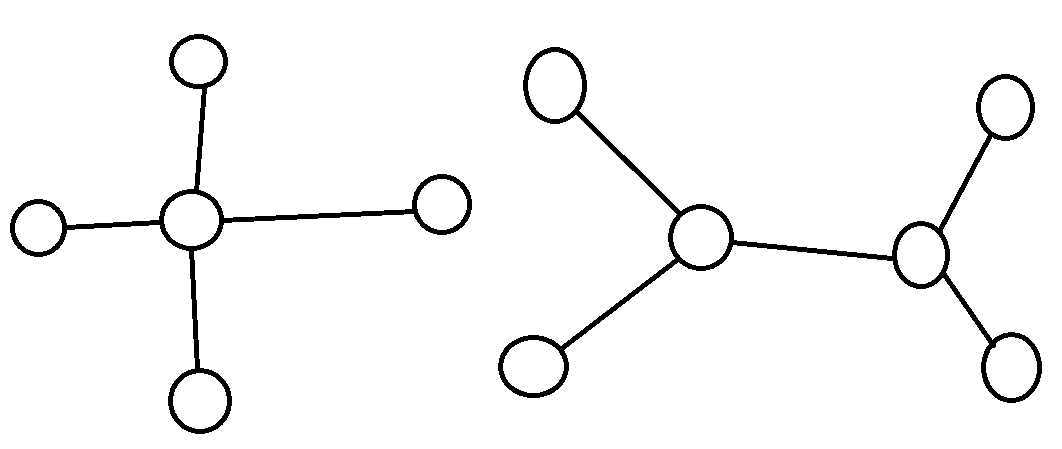
其中“长度相近”指长度均为p或p+1,且长度为p的链只有一条或长度为p+1的链只有一条。
预处理出每一个点连出所有边引出链的最大长度,对于一个点P,设其引出第k长的链长度为len(p,k),则$ans_{len(p,k)} \geq k$。
原文:https://www.cnblogs.com/2005lz/p/13121667.html