与之前学过的梯度下降等不同，Logistic回归是一类分类问题，而前者是回归问题。回归问题中，尝试预测的变量y是连续的变量，而在分类问题中，y是一组离散的，比如y只能取{0,1}。
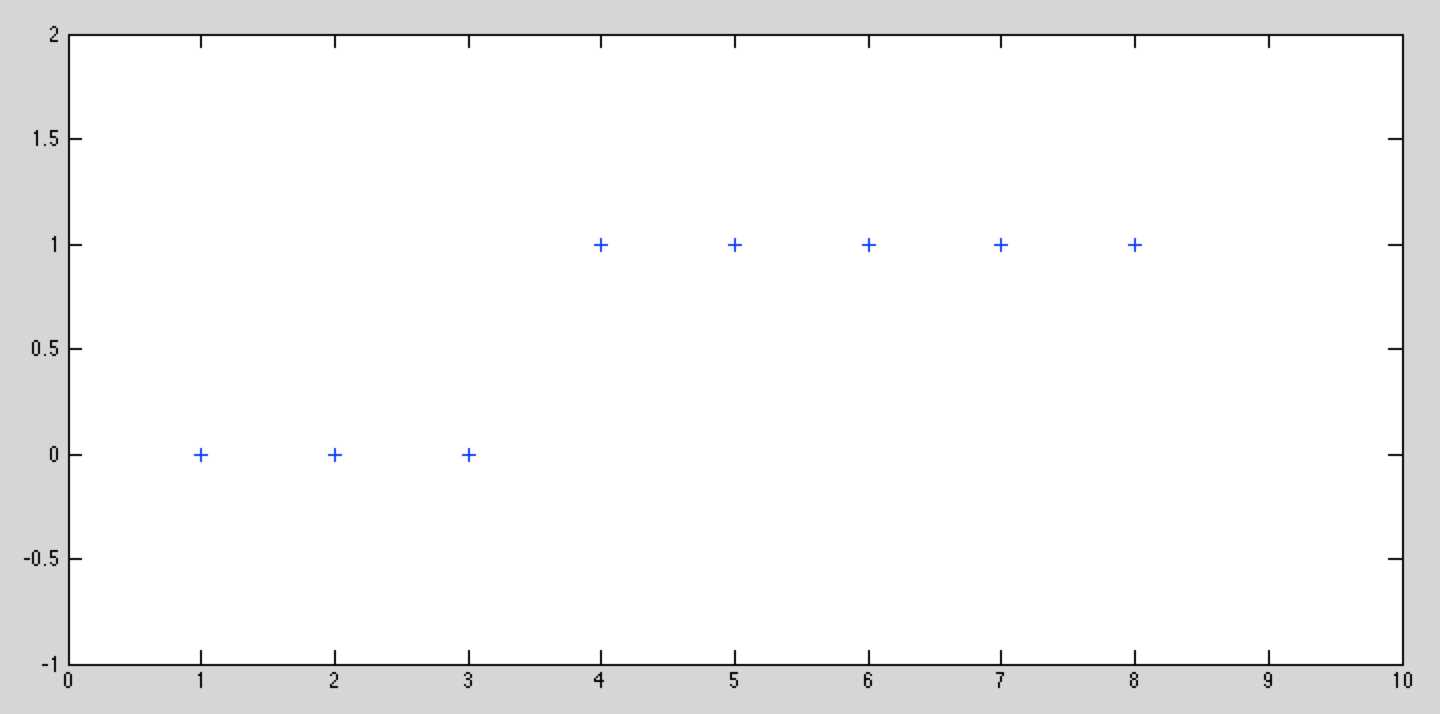
假设一组样本为这样如图所示，如果需要用线性回归来拟合这些样本，匹配效果会很不好。对于这种y值只有{0,1}这种情况的，可以使用分类方法进行。
假设
其中定义Logistic函数(又名sigmoid函数)：
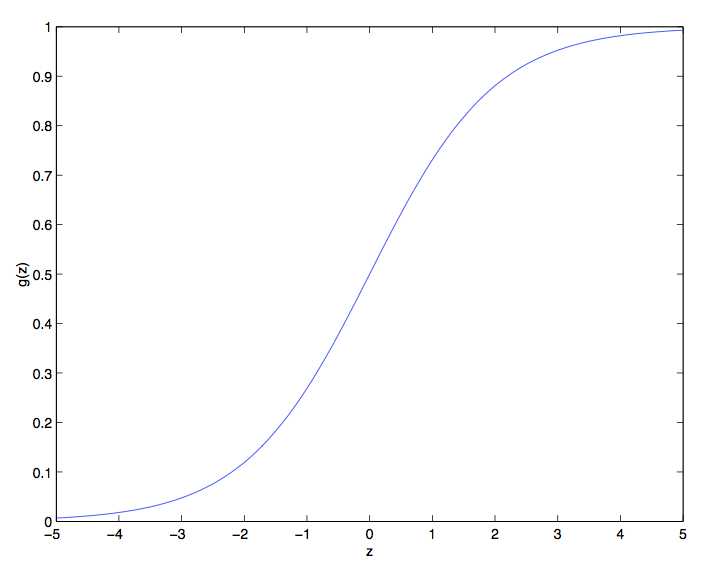
下图是Logistic函数g(z)的分布曲线，当z大时候g(z)趋向1，当z小的时候g(z)趋向0，z=0时候g(z)=0.5,因此将g(z)控制在{0,1}之间。其他的g(z)函数只要是在{0,1}之间就同样可以，但是后续的章节会讲到，现在所使用的sigmoid函数是最常用的
假设给定x以为参数的y=1和y=0的概率：
可以简写成：
假设m个训练样本都是独立的，那么θ的似然函数可以写成：
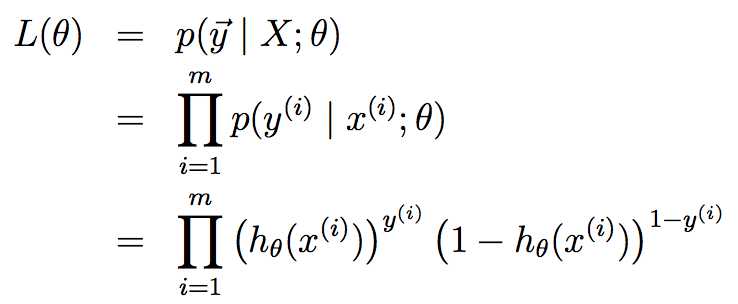
对L(θ)求解对数最大似然值：
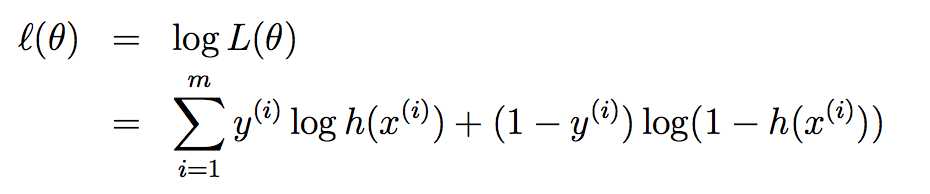为了使似然性最大化，类似于线性回归使用梯度下降的方法，求对数似然性对
注意：之前的梯度下降算法的公式为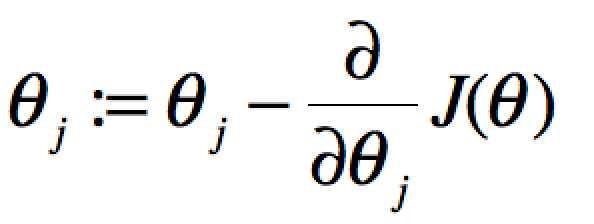
。这是是梯度上升，Θ:=Θ的含义就是前后两次迭代(或者说前后两个样本)的变化值为l(Θ)的导数。
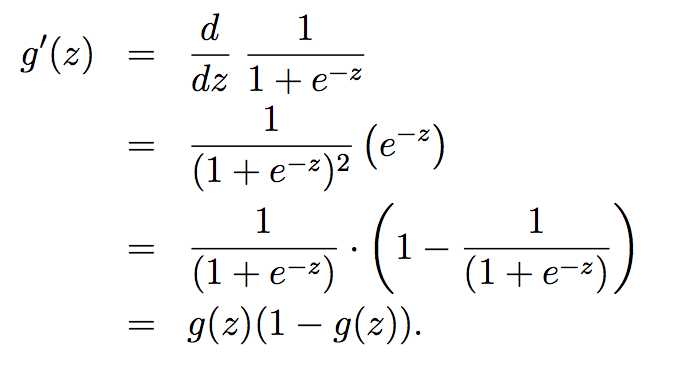
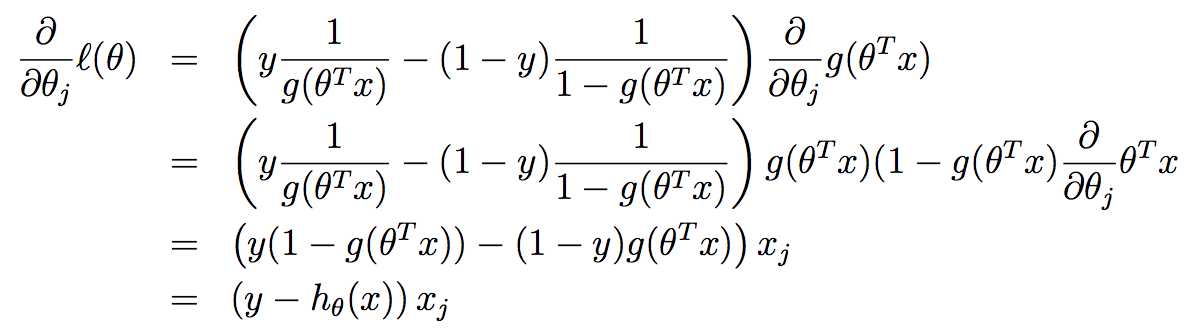
则
即类似上节课的随机梯度上升算法，形式上和线性回归是相同的，只是符号相反，
原文：http://www.cnblogs.com/rcfeng/p/3967445.html
