栈Stack |队列Queue| 双端队列Deque| 优先队列PriorityQueue
堆栈和队列特点: 1. Stack - First In Last Out(FILO) 先入后出,先进来的被压入栈底 .Array or Linked List 2. Queue - First In First Out(FIFO) 排队时先来先出 .Array or Doubly Linked List
Stack中文名可叫堆栈,不能叫堆,堆是heap
手写栈堆比较少了,很多语言在标准库都实现了。
栈 Stack -先入后出的容器结构
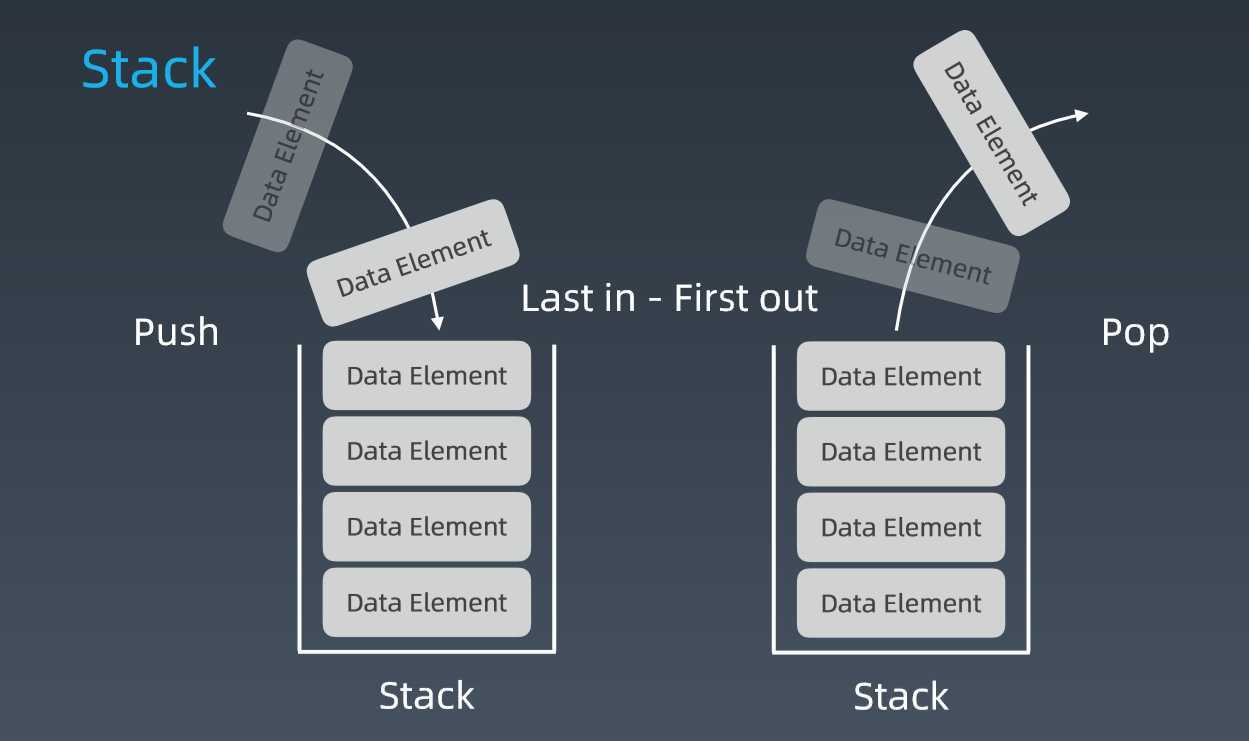
栈:查询 O(n),平均情况,要看它栈中栈底的元素,要清空了才能看到。
插入和删除它的栈顶元素只需要一次性操作,时间复杂度是O(1)。
从刚才栈的定义里,我们可以看出,栈主要包含两个操作,入栈和出栈,也就是在栈顶插入一个数据和从栈顶删除一个数据。理解了栈的定义之后,我们来看一看如何用代码实现一个栈。
实际上,栈既可以用数组来实现,也可以用链表来实现。
用数组实现的栈,叫作顺序栈,用链表实现的栈,叫作链式栈。
// 基于数组实现的顺序栈
public class ArrayStack {
private String[] items; // 数组
private int count; // 栈中元素个数
private int n; // 栈的大小
// 初始化数组,申请一个大小为 n 的数组空间
public ArrayStack(int n) {
this.items = new String[n];
this.n = n;
this.count = 0;
}
// 入栈操作
public boolean push(String item) {
// 数组空间不够了,直接返回 false,入栈失败。
if (count == n) return false;
// 将 item 放到下标为 count 的位置,并且 count 加一
items[count] = item;
++count;
return true;
}
// 出栈操作
public String pop() {
// 栈为空,则直接返回 null
if (count == 0) return null;
// 返回下标为 count-1 的数组元素,并且栈中元素个数 count 减一
String tmp = items[count - 1];
--count;
return tmp;
}
}
不管是顺序栈还是链式栈,我们存储数据只需要一个大小为 n 的数组就够了。在入栈和出栈过程中,只需要一两个临时变量存储空间,所以空间复杂度是 O(1)。
注意,这里存储数据需要一个大小为 n 的数组,并不是说空间复杂度就是 O(n)。因为,这 n 个空间是必须的,无法省掉。所以我们说空间复杂度的时候,是指除了原本的数据存储空间外,算法运行还需要额外的存储空间。
空间复杂度分析是不是很简单?时间复杂度也不难。不管是顺序栈还是链式栈,入栈、出栈只涉及栈顶个别数据的操作,所以时间复杂度都是 O(1)。
如何基于栈实现浏览器的前进和后退功能?
当你依次访问完一串页面 a-b-c 之后,点击浏览器的后退按钮,就可以查看之前浏览过的页面 b 和 a。当你后退到页面 a,点击前进按钮,就可以重新查看页面 b 和 c。但是,如果你后退到页面 b 后,点击了新的页面 d,那就无法再通过前进、后退功能查看页面 c 了。
如何实现浏览器的前进、后退功能?其实,用两个栈就可以非常完美地解决这个问题。
我们使用两个栈,X 和 Y,我们把首次浏览的页面依次压入栈 X,当点击后退按钮时,再依次从栈 X 中出栈,并将出栈的数据依次放入栈 Y。当我们点击前进按钮时,我们依次从栈 Y 中取出数据,放入栈 X 中。当栈 X 中没有数据时,那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据,那就说明没有页面可以点击前进按钮浏览了。
后进者先出,先进者后出,这就是典型的“栈”结构。
从栈的操作特性上来看,栈是一种“操作受限”的线性表,只允许在一端插入和删除数据。
事实上,从功能上来说,数组或链表确实可以替代栈,但你要知道,特定的数据结构是对特定场景的抽象,而且,数组或链表暴露了太多的操作接口,操作上的确灵活自由,但使用时就比较不可控,自然也就更容易出错。
当某个数据集合只涉及在一端插入和删除数据,并且满足后进先出、先进后出的特性,我们就应该首选“栈”这种数据结构。
① 栈在函数调用中的应用,经典的一个应用场景就是函数调用栈。
操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成“栈”这种结构, 用来存储函数调用时的临时变量。每进入一个函数,就会将临时变量作为一个栈帧入栈,当被调用函数执行完成,返回之后,将这个函数对应的栈帧出栈。
② 栈在表达式求值中的应用
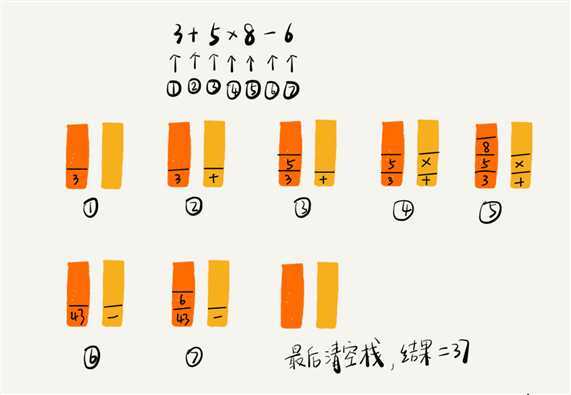
我们再来看栈的另一个常见的应用场景,编译器如何利用栈来实现表达式求值。
为了方便解释,我将算术表达式简化为只包含加减乘除四则运算,比如:34+13*9+44-12/3。
③ 栈在括号匹配中的应用
假设表达式中只包含三种括号,圆括号 ()、方括号 [] 和花括号{},并且它们可以任意嵌套。比如,{[{}]}或 [{()}([])] 等都为合法格式,而{[}()] 或 [({)] 为不合法的格式。那我现在给你一个包含三种括号的表达式字符串,如何检查它是否合法呢?
这里也可以用栈来解决。我们用栈来保存未匹配的左括号,从左到右依次扫描字符串。当扫描到左括号时,则将其压入栈中;当扫描到右括号时,从栈顶取出一个左括号。如果能够匹配,比如“(”跟“)”匹配,“[”跟“]”匹配,“{”跟“}”匹配,则继续扫描剩下的字符串。如果扫描的过程中,遇到不能配对的右括号,或者栈中没有数据,则说明为非法格式。
当所有的括号都扫描完成之后,如果栈为空,则说明字符串为合法格式;否则,说明有未匹配的左括号,为非法格式。
思考
内存中的堆栈和数据结构堆栈不是一个概念,可以说内存中的堆栈是真实存在的物理区,数据结构中的堆栈是抽象的数据存储结构。
内存空间在逻辑上分为三部分:代码区、静态数据区和动态数据区,动态数据区又分为栈区和堆区。
代码区:存储方法体的二进制代码。高级调度(作业调度)、中级调度(内存调度)、低级调度(进程调度)控制代码区执行代码的切换。
静态数据区:存储全局变量、静态变量、常量,常量包括final修饰的常量和String常量。系统自动分配和回收。
栈区:存储运行方法的形参、局部变量、返回值。由系统自动分配和回收。
堆区:new一个对象的引用或地址存储在栈区,指向该对象存储在堆区中的真实数据。
栈的应用场景
1) 子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中。
2) 处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
3) 表达式的转换与求值(实际解决)。
4) 二叉树的遍历。
5) 图形的深度优先(depth一first)搜索法。
1) 用数组模拟栈的使用,由于栈是一种有序列表,当然可以使用数组的结构来储存栈的数据内容,
下面我们就用数组模拟栈的出栈,入栈等操作。
2) 实现思路分析,并画出示意图
代码实现:

import scala.io.StdIn object ArrayStackDemo { def main(args: Array[String]): Unit = { //测试栈 val stack = new ArrayStack(4) var key = "" while (true) { println("list: 显示栈") println("push: 入栈") println("pop: 出栈") println("peek: 查看栈顶") key = StdIn.readLine() key match { case "list" => stack.list() case "push" => println("请输入一个数") val value = StdIn.readInt() stack.push(value) case "pop" => val res = stack.pop() if(res.isInstanceOf[Exception]) { println(res.asInstanceOf[Exception].getMessage) }else{ printf("取出栈顶的元素是%d", res) } case "peek" => val res = stack.peek() if(res.isInstanceOf[Exception]) { println(res.asInstanceOf[Exception].getMessage) }else{ printf("栈顶的元素是%d", res) } //默认处理 } } } } //ArrayStack 表示栈 class ArrayStack(arrMaxSize:Int) { var top = -1 val maxSize = arrMaxSize val arr = new Array[Int](maxSize) //判断栈空 def isEmpty(): Boolean = { top == -1 } //栈满 def isFull(): Boolean = { top == maxSize - 1 } //入栈操作 def push(num:Int): Unit = { if(isFull()) { println("栈满,不能加入") return } top += 1 arr(top) = num } //出栈操作 def pop(): Any = { if(isEmpty()) { return new Exception("栈空,没有数据") } val res = arr(top) top -= 1 return res } //遍历栈 def list(): Unit = { if(isEmpty()) { println("栈空") return } //使用for for(i <- 0 to top reverse) { //逆序打印 printf("arr(%d)=%d\n", i, arr(i)) } println() } //查看栈的元素是什么,但是不会真的把栈顶的数据弹出 def peek(): Any = { if(isEmpty()) { return new Exception("栈空") } return arr(top) } }
队列,排队,先来先出,依次排队。
栈:查询 O(n),平均情况,要看它栈中栈底的元素,要清空了才能看到。
插入和删除它的栈顶元素只需要一次性操作,时间复杂度是O(1)。
队列:与栈类似, 查询是O(n),插入和删除是O(1)。
查询操作O(n),因为它是元素无序的 ,就必须把这个数据结构遍历一遍
把它想象成排队买票,先来的先买,后来的人只能站末尾,不允许插队。先进者先出,这就是典型的“队列”。
我们知道,栈只支持两个基本操作:入栈 push()和出栈 pop()。
队列跟栈非常相似,支持的操作也很有限,最基本的操作也是两个:
入队 enqueue(),放一个数据到队列尾部;出队 dequeue(),从队列头部取一个元素。
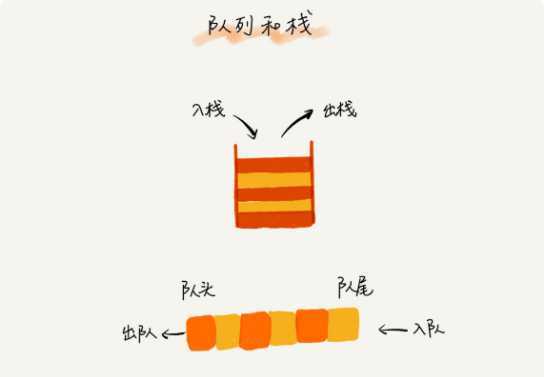
所以,队列跟栈一样,也是一种操作受限的线性表数据结构。
作为一种非常基础的数据结构,队列的应用也非常广泛,特别是一些具有某些额外特性的队列,比如循环队列、阻塞队列、并发队列。它们在很多偏底层系统、框架、中间件的开发中,起着关键性的作用。比如高性能队列 Disruptor、Linux 环形缓存,都用到了循环并发队列;Java concurrent 并发包利用 ArrayBlockingQueue 来实现公平锁等。
队列跟栈一样,也是一种抽象的数据结构。它具有先进先出的特性,支持在队尾插入元素,在队头删除元素,那究竟该如何实现一个队列呢?
跟栈一样,队列可以用数组来实现,也可以用链表来实现。用数组实现的栈叫作顺序栈,用链表实现的栈叫作链式栈。
同样,用数组实现的队列叫作顺序队列,用链表实现的队列叫作链式队列。
1) 队列是一个有序列表,可以用数组或是链表来实现。数据结构就是研究数据组织形式,并且为算法打基础。
2) 遵循先入先出的原则。即:先存入队列的数据,要先取出。后存入的要后取出
3) 示意图:(使用数组模拟队列示意图)
4) 线性结构,一对一关系
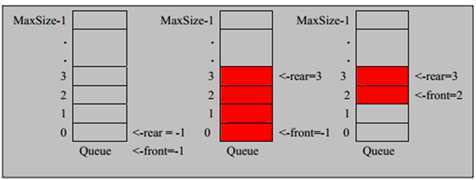
数组模拟队列
rear 表示队列尾,rear 指向队列的最后一个元素
front 表示队列的头,表示指向队列的第一个元素的前一个位置
1) 将尾指针往后移:rear+1 , front == rear 【队列空】
2) 若尾指引 rear 小于队列的最大下标 MaxSize-1,则将数据存入 rear所指的数组元素中,否则无法存入数据。 rear == MaxSize - 1[队列满]
代码实现:

object ArrayQueueDemo { def main(args: Array[String]): Unit = { //创建一个队列对象 val queue = new ArrayQueue(3) var key = "" //接收用户的输入 //简单写个菜单 while (true) { println("show : 显示队列") println("add: 添加数据到队列") println("get: 从队列头取出元素") println("peek: 查看队列头元素") key = StdIn.readLine() key match { case "show" => queue.showQueue() case "add" => println("请输入一个数吧") val value = StdIn.readInt() queue.addQueue(value) case "get" => val res = queue.getQueue()//取出 //判断res 的类型 if(res.isInstanceOf[Exception]) { //输出异常信息 println(res.asInstanceOf[Exception].getMessage) }else { printf("取出的队列头元素是%d", res) } case "peek" => val res = queue.peek()//查看 //判断res 的类型 if(res.isInstanceOf[Exception]) { //输出异常信息 println(res.asInstanceOf[Exception].getMessage) }else { printf("队列头元素是%d", res) } } } } } //定义一个类ArrayQueue 表队列 //该类会实现队列的相关方法 //数据结构 创建-遍历-测试-修改-删除 class ArrayQueue(arrMaxSize: Int) { val maxSize = arrMaxSize val arr = new Array[Int](maxSize) //队列的数据存放的数组 var front = -1 // 表示指向队列的第一个元素的前一个位置 var rear = -1 //表示指向队列的最后个元素 //查看队列的头元素,但是不取出 def peek(): Any = { if(isEmpty()) { return new Exception("队列空,没有数据返回"); } return arr(front + 1) } //判断队列是否满 def isFull(): Boolean = { rear == maxSize - 1 } //判断队列是空 def isEmpty(): Boolean = { rear == front } //从队列中取出数据 //异常时可以加入业务逻辑 def getQueue(): Any = { if(isEmpty()) { return new Exception("队列空,没有数据返回"); } //将front 后移一位 front += 1 return arr(front) } //给队列添加数据 def addQueue(num: Int): Unit = { if (isFull()) { println("队列满,不能加入!!") return } //添加时调整rear //1. 先将rear 后移 rear += 1 arr(rear) = num } //遍历队列 def showQueue(): Unit = { if (isEmpty()) { println("队列空!!") return } for (i <- (front + 1) to rear) { printf("arr(%d)=%d\t", i, arr(i)) } println() } }
数组模拟环形队列
1) 尾索引的下一个为头索引时表示队列满,即将队列容量空出一个作为约定,这个在做判断队列满的时候需要注意 (rear + 1) % maxSize == front 满] rear == front [空]
2) 测试示意图:
3) 代码实现

object CircleArrayQueueDemo { def main(args: Array[String]): Unit = { //创建一个队列对象 val queue = new CircleArrayQueue(4) var key = "" //接收用户的输入 //简单写个菜单 while (true) { println("show : 显示队列") println("add: 添加数据到队列") println("get: 从队列头取出元素") println("peek: 查看队列头元素") key = StdIn.readLine() key match { case "show" => queue.showQueue() case "add" => println("请输入一个数吧") val value = StdIn.readInt() queue.addQueue(value) case "get" => val res = queue.getQueue()//取出 //判断res 的类型 if(res.isInstanceOf[Exception]) { //输出异常信息 println(res.asInstanceOf[Exception].getMessage) }else { printf("取出的队列头元素是%d", res) } case "peek" => val res = queue.peek()//查看 //判断res 的类型 if(res.isInstanceOf[Exception]) { //输出异常信息 println(res.asInstanceOf[Exception].getMessage) }else { printf("队列头元素是%d", res) } } } } } //定义一个类CircleArrayQueue 表环形队列 //该类会实现队列的相关方法 //数据结构 创建-遍历-测试--删除 class CircleArrayQueue(arrMaxSize: Int) { val maxSize = arrMaxSize val arr = new Array[Int](maxSize) //队列的数据存放的数组 var front = 0 // front 初始化 = 0 , front 约定 指向队列的头元素 var rear = 0 // rear 初始化为 = 0, rear 指向队列的 最后元素的后一个位置, 因为需要空出一个位置做约定 //判断队列是否满 def isFull(): Boolean = { (rear + 1) % maxSize == front } //判断队列是空,和前面一样 def isEmpty(): Boolean = { rear == front } //从队列中取出数据 //异常时可以加入业务逻辑 def getQueue(): Any = { if(isEmpty()) { return new Exception("队列空,没有数据返回"); } //返回front指向的值 //1. 先把 arr(front) 保存到一个临时变量 //2. front += 1 //3. 返回临时变量 var temp = arr(front) front = (front + 1) % maxSize return temp } //查看队列的头元素,但是不取出 def peek(): Any = { if(isEmpty()) { return new Exception("队列空,没有数据返回"); } return arr(front) } //给队列添加数据 def addQueue(num: Int): Unit = { if (isFull()) { println("队列满,不能加入!!") return } //先把数据放入到arr(rear) 位置,然后后移rear arr(rear) = num rear = (rear + 1) % maxSize } //遍历队列 def showQueue(): Unit = { if (isEmpty()) { println("队列空!!") return } //动脑筋 //1. 从front 开始打印 , 打印几个元素 for (i <- front until (front + size()) ) { printf("arr(%d)=%d\t", (i % maxSize) , arr(i % maxSize)) } println() } //求出当前队列共有多少个数据 def size(): Int = { (rear + maxSize - front) % maxSize } }
队列在线程池等有限资源池中的应用
CPU 资源是有限的,任务的处理速度与线程个数并不是线性正相关。相反,过多的线程反而会导致 CPU 频繁切换,处理性能下降。所以,线程池的大小一般都是综合考虑要处理任务的特点和硬件环境,来事先设置的。
当我们向固定大小的线程池中请求一个线程时,如果线程池中没有空闲资源了,这个时候线程池如何处理这个请求?是拒绝请求还是排队请求?各种处理策略又是怎么实现的呢?
可理解为一个queue和stack的结合体,一个简单的队列,但它的头 和 尾都可以进行元素的出和进
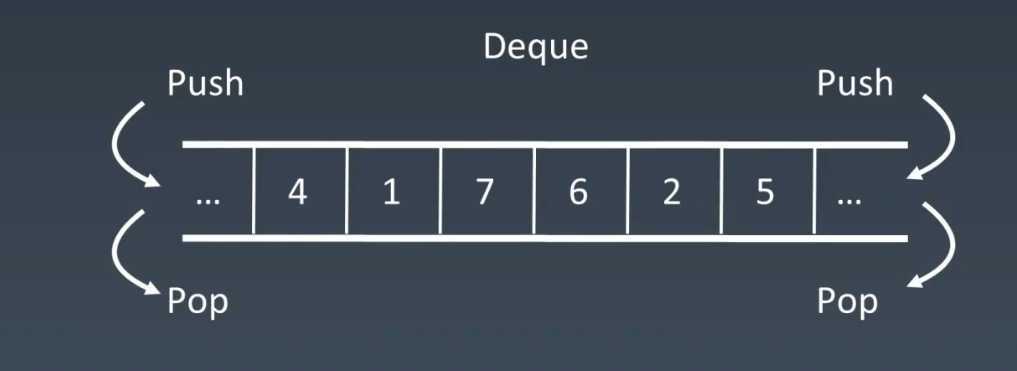
插入和删除都是 O(1) 操作,查询是O(n) ;
插入O(1)
取出 O(logN) -- 按照元素的优先级取出;(取出相比栈和队列变慢了,好处是它的顺序不再是FIFO或者FILO,而是按照元素的优先级取出,VIP先行)
底层具体实现的数据结构较为多样和复杂:堆heap、 二叉搜索树bst、 treap
原文:https://www.cnblogs.com/shengyang17/p/13124538.html