6.4
无向图的储存用一维数组(节省一半空间)

一、邻接矩阵
1.邻接矩阵的好处
①直观、简单、容易理解
②方便检查一对顶点之间是否存在边
③方便查找任意一顶点的所有邻接点
④方便计算任一顶点的“度”

2.邻接矩阵的不好
①浪费空间(点多边少时) 但对稠密图还是合算的
②浪费时间(对于稀疏图 统计边时)
基于邻接矩阵创建无向带权图


二、邻接表(链表的集合)(足够稀疏才合算)
1.好处
①方便找所有邻接点
②节约稀疏图空间(需要N个头指针和2E个结点(每个结点至少两个域))
③方便计算无向图的度
三、图的遍历
1.深度优先搜索 DFS
访问一个点然后从该点出发;访问该点未被访问的邻接点,该邻接点成为新顶点;重复上一步骤;待新顶点没有未被访问的邻接点时,返回上一点,查找并访问未被访问的邻接点;重复上一步骤,直至全部点都被访问。
2.广度优先搜索 BFS
访问一个点然后从该点出发;访问该点的所有邻接点,先被访问的邻接点先成为新顶点,访问ta的邻接点,然后后被访问的邻接点成为新顶点,访问ta的所以邻接点,以此类推,直至所有点被访问完成。(感觉和层次遍历类似)
四、最短路径
(一)单源最短路
有权图:看权值 按照递增的顺序找出到各个顶点的最短路(Dijkstra算法不能解决有负边)

无权图:权值为1的有权图
(二)多源
最小生成树
1. 普里姆算法 Prim
从某点出发,将与它关联的边权值最小的顶点加入集合,在集合内的点中选择与它们相关联的边权值最小的顶点,以此类推。不一定按点进入的顺序找接下来的点 出现过的点不能再选
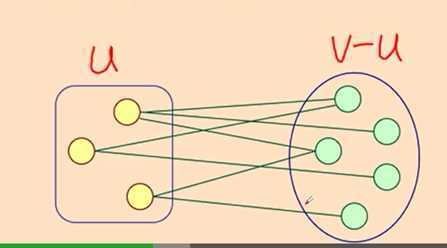
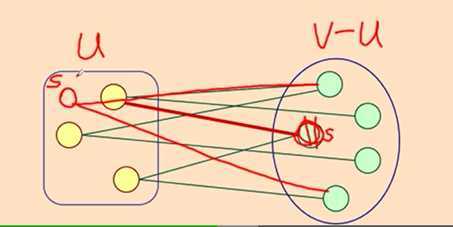
2. 克鲁斯卡尔算法 Kruskal
原文:https://www.cnblogs.com/f0121t0131/p/13126354.html