这篇文章是我阅读《大话数据结构》前两章,和阅读相关一些博客的学习笔记总结,主要介绍一下数据结构和算法是什么,有什么用。
在介绍数据结构之前,我们先来介绍一些前置知识,因为计算机的专业词汇都是英文的,我们又是第一次接触这个词汇,而对其进行翻译经常会造成一些理解上的偏差和误导,所以我尽量在涉及专业词汇时使用英文词汇。
计算机只能存储二进制文件,这是我们都知道的,因为硬件上的构造所致,所以计算机最终处理的一些信息都是二进制文件。就这么说可能不怎么容易理解,我们来实际看一下吧
// 新建文件
touch a.c
// 编辑
vim a.c
//输入
#include <stdio.h>
int main(void) {
printf("hello world");
return 0;
}
// 编译
gcc a.c -o b
// 执行
./b // 输出 hello world, 说明我们编译成功了
// 查看二进制文件,使用 xxd 命令,输出十进制
xxd -b b
如果成功了,我们会看到
0000403e: 00000000 00000000 00000001 00000000 00000000 00000000 ......
00004044: 00000000 00000000 00000000 00000000 00000000 00000000 ......
0000404a: 00000000 00000000 00000000 00000000 00000000 00000000 ......
00004050: 00010001 00000000 00000000 00000000 00000011 00000000 ......
00004056: 00000000 00000000 00000000 00000000 00000000 00000000 ......
0000405c: 00000000 00000000 00000000 00000000 00000000 00000000 ......
我们可以清晰的看到,二进制文件的确是 0 1 组成的。那么对于计算机都是些 0 1, 那我们人类该怎么对待这些 0 1 呢?
或许我们该思考一下,我们发明计算机是为了什么,我们每天都在使用计算机,手机,电梯,冰箱。。真如同我们思考物理的未来一样,我们去探索这些并不是为了真理,而是为了解决我们所遇到的实际的问题。那么要解决问题,就要模拟实际问题,然后再是解决问题。所以计算机就面对着一个很重要的任务:输入信息,处理信息,输出信息。信息,也就是我们要讲的 data。
我们刚刚说了计算机只能存放和处理二进制信息,而又面临则模拟世界的重任,而我们这个世界也是又小小的原子组成许多不同类型的分子,然后又组成各种各样的东西,最终形成了我们现在的世界,所以我们同样需要使用这些二进制来创造一些 type, 也就是 data type,来作为一些基础来模拟现实。
我们刚刚引入了 data type 的必要性,现在我们就来谈谈它们在具体的语言中的实现。我们知道计算机都是二进制存储的,所以在早期编程人员们也只能输出输出二进制数据,也就是使用机械语言。慢慢的人们发现有一些操作是经常做的,所以为了提高效率,把一些常用的操作简写成一些字母,然后使用这些字母来经常编程,这些字母就是汇编语言。但是我们知道这些语言都是直接和机器打交道的,让我们这些使用自然语言交流的人很不容易理解,所以为了便于人们能够理解,就慢慢出现了一些模仿自然语言的高级语言,如同 c 语言,这之后又出现许多编程范式,创建了许多语言,有着各种各样的应用场景。
我们简要知道了语言的发展,而现在我们一般都使用高级语言与机器交互,我们又说了机器要模拟实际,所以高级语言一般都内置了一些基本的 data type, 正如同英语有 26 个字母一样,有些类型是不可分割的,而又如同我们可以自由使用字母组合新单词,我们也可以使用各种 data type 来组成其他的 type。
具体到高级语言,如有 int, bool, float, char,num, pointer 这些不可分割的基础 type,也有在不同机器上体现差距的 int32,int64 等等。也有 array, struct, map 等多个 type 组合类型。
我们刚刚明白了 data type 是怎么来的,现在我们来讲一下 data type 中比较常见的一个概念。我们说过,语言中的基本 type 可以由其他的 type 注册,那么当我们使用一个 type 时,这个 type 背后的原理都是对我们来说是不可见的,这个 type 就可以说是 abstract 的,我们使用计算机模拟这个时间,比如现在要模拟一个学生,我们可能会定义一个学生类,然后给它声明一些变量属性,给它加一些动作方法,但我们操作这个学生类时,这个 type 既在原理上对我们来说是封装好的,用这种模拟的方式来模拟现实中的事务,这也是一种抽象,我们也可以说这个 type 是 abstract 的,所以无论是从存储的原理来说,还是模拟现实来说,任何 type 都是 abstract 的,所以可以说每个 data type 都是 abstract data type(ADT).
我们现在应该能够理解 data type 在一门语言中的地位了,而实际在一门语言中怎么设计,就要看 type system 这门学科了。我们在这里简单介绍一下。 type system 就如同 operation system, file system 一般,是具体研究某门知识的学科,这里就是研究在语言中 type 怎么设计,怎么存储,怎么运用,怎么检查,怎么转换等知识。
我们作为普通的程序猿,一般接触到得比较多的就是 type declaration, type checking 和 type conversion 相关的知识了。
比如我们使用在 c 中,要声明一个变量
int a;
需要显式的表明这个类型是什么,而在 type 中,我们则可以不显式的声明,编译器会根据赋值的内容去自动推断
a = 1;
我们使用了不同的 type, 那么计算机也需要检查 type 对不对,我们知道一般的软件构建过程是 编写(edit) -> 编译(compile) -> 链接(link) -> 装载 -> 运行(run)
而一般 type checking 发生在 compile 或 run 期间。发生在 complie 的就叫 Statically checked language,而发生在 run 期间的就叫 Dynamically checked language。像 js, python,php 就是动态语言,而 c,java,c++ 等就是静态语言。
除了 type checking 外,type conversion 也是我们经常遇见的,一般对那些 type checking 限制比较弱,可以隐式的类型转换的语言,我们叫 Weakly checked language,比如 c, python, js
int a;
a = ‘b‘;
这种直接不同 type 间可以直接 convert ,具体的转换过程由编译器自己做。
而一般对那些 type checking 限制比较强,需要显式的类型转换的语言,我们叫 Strongly checked language,比如 go, java
var a int
a = "b"
这样直接转换会报 error,需要使用特殊的函数才行。 type system 是一门庞大的学科,这里只是简单介绍一下,要深入学习还需要读更多的书,做更多的实践。
我们前面讲了 data type 的来由,我们一般直接就拿不同 type 的 data 开始干活,比如直接声明个 int a 就开始赋值判断什么的,但是我们也知道,除了直接使用 data 做事外,data 间也有一些关系,这就是我们要讲的 data structure.
我们先来讲一下 data 间在逻辑上有哪些结构,就像我们中学学过的函数图像一样,data 间有线性结构(linear structure) 和非线性结构(nonlinear structure) 这两种。
线性结构(linear structure) 的我们一般叫线性表(Linear list),data 间一个连着一个,一对一的关系,就是 linear list ,而没有 data 的 linear list 我们一般叫空表。
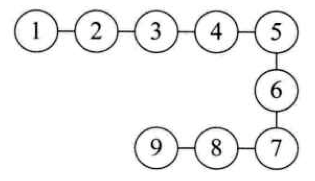
非线性结构(nonlinear structure) 有树(Tree), 图(Graph) 这两种。
data 前面最多连接一个,后面可以连接多个的叫 tree, 讲究 data 间一对多。
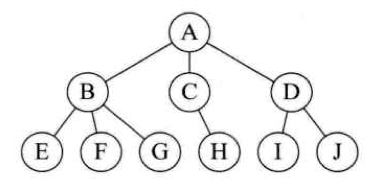
data 前面后面都可以连接多个的,我们叫 graph, data 间是多对多的关系。
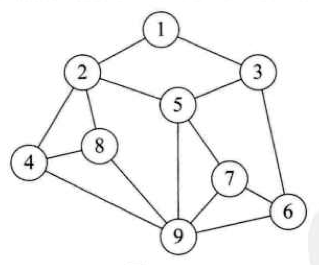
data 间从逻辑上来说就只有上面那三种关系,现在我们来看一下 data 间物理上的关系,我们知道 data 都是要存在存储介质上的,一般我们说的是内存,所以 data 在物理上的关系就是在内存上是什么关系。所以物理结构也叫存储结构。
在物理上存储,两个 data 只有两种情况,相连或不相连,所以对于多个 data 来说也只有两种情况,顺序存储结构和链式存储结构。
顺序存储结构:data 在内存(或其他存储载体)上,连续分配内存空间,要查询下一个 data,只需查看下一个内存单元地址的 data 即可

链式存储结构:data 在内存单元生分布没有规律,因此要查询逻辑上的下一个 data,需要知道下一个 data 在哪,于是需要知道下一个 data 的内存地址,就会在这个 data 的地方存放下一个 data 的内存地址,也就是指针。
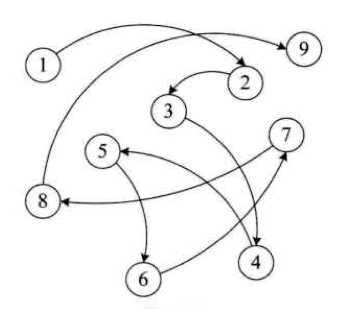
data 的 structure 其实就只有上面这些情况,其他的结构都只是这上面的推广。如逻辑上线性的 data 如果在物理上也线性,也就是连续分配内存空间,那就是顺序表,我们常使用的 string, array,slice 其实就是顺序表中的一种,如果逻辑上线性的 data 如果在物理上非线性,那就是链表。我们常说的栈则是限定仅在表尾进行插入和删除操作的线性表。队列则是只允许在一端进行插入操作、而在另一端进行删除操作的线性表。还有我们常说的二叉树也只是只有两个分支的 tree, 堆则是一种特殊二叉树等等。
理解了 data 间的关系,再具体去学习的时候就能比较容易的理解一些数据结构的性质,比如因为线性表在内存上连续分配,所以可以根据首地址和偏移量拿到每个 data 的地址,所以线性表的查询算法时间复杂度是 O(1), 同样理解了基础的结构之后,对于一些新的,未知的数据结构也能知道大概是什么样的,比如以前可能完全没有听说过队列,但是如果说它是个特殊的线性表,那就更容易理解些。
我们现在从 data 开始,一直说道了 data structure, 不要完了我们为什么要说这些。回想一下,我们为什么要去学习 data 呢,因为这是计算机对信息的表达,和处理方式,那我们为什么要去学习计算机呢,你可能还记得,我们学习计算机不是为了追求真理,而是为了解决现实中,我们实际遇到的问题,而算法(algorithm)就是这么一个东西,算法就是解决问题的方法。
算法是一种抽象的概念,只要能够解决一个问题,那它就是一个算法,而在计算机中是使用指令来执行命令的,所以算法是又一些指令组成,能够解决 问题的指令级。我们理解为步骤就行了,比如一个经典的问题:怎样才能把一头大象装进冰箱?
我们现在有问题:怎样才能把一头大象装进冰箱,然后要给出这个问题的方法,也就是算法的话,这里有一个很经典的回答
1. 把冰箱门打开
2. 把大象装进去
3. 把冰箱门关上
现在我们解决了问题(怎样才能把一头大象装进冰箱),又是一些步骤(指令)的集合,所以这就是一个算法。
一般一个问题不只一个算法,比如刚刚这个问题,我们可以把大象切成肉片(orz), 然后再打开冰箱把它装进去,这也是一个算法,不同算法间也有效率高低之分,这个我们等会再说。
我们刚刚也没有说要使用怎样的语言来解决这个问题,我们可以用自然语言,可以用伪代码,也可以用其他高级语言,这并不是一个需要过于担心的问题。
我们引入了算法是什么,来看一下比较规范的定义吧
输入输出:可以没有输入,但是需要有输出参数,可以是打印,或者返回值 有穷性:执行有限的步骤,在可接受的时间内完成
确定性:每个步骤都没有二义性,都有明确唯一的意义
可行性:算法可以转换为程序上机运行,并得到正确的结果
算法要有输入输出,要每个步骤都有明确的意义,要在可以接受的时间内完成,要可以实际用语言实现。
正确性:算法能够成功解决问题,没有语法错误和语义错误
可读性: 算法可读性高,人们便于理解
健壮性:对不合法输入能够做出处理
效率: 时间复杂度低,算法花的时间少
占用内存: 空间复杂度低,算法占用的内存少
算法要没有语法、语义错误,能成功解决问题,要便于人们理解,对于不合法输入能够正确处理,花费时间和内存少,效率高。
我们说了一个问题可以有不同的算法,那么怎么判定一个算法的好坏就很重要,也就是怎么判断一个算法效率的高低。
一个算法要执行的话,会花费空间(占用内存)(空间复杂度),时间(时间复杂度),以前的内存价格高,现在我们对内存的要求没有那么高了,所以一般只看花费的时间,但是如何看花费了多少时间呢?
事后统计:算法写完之后,通过测试大量数据看 run 的时间来比对效率,这种方法对硬件的要求,软件的要求,问题规模等要求比较高,而且作为统计数据,从科学上没有那么科学
事前分析:通过判断执行语句的次数,来统计估量时间复杂度,需要测试的数据越多,次数的变化会体现出算法的效率
一般来说就这么两种方法,我们知道实际算法的效率
计算机执行每条指令的速度 -> 硬件层面
编译产生的代码质量 -> 软件层面
算法的好坏 (算法使用的策略)
问题规模
事后统计要四个都要看,而事前分析只需要看算法的好坏和问题规模,所以要实际测量算法效率,事前分析比较好。但是只是分析的话,又不能实际 run 一下看消耗时间,所以可以用实际执行的语句次数来表示,这样能用数学证明算法的效率优劣。要使用实际执行的语句次数来表示时间,这里就要引入时间复杂度的概念
公式:T(n) = O(f(n))
n: 问题规模
f(n): 执行指令次数
T(n): 时间复杂度
O () :一种运算方式,作用就是去除其他项,包括与最高项相乘的常数,只保留最高项
比如这个算法
int i; // 1 此
for(i = 0 ; i < n ; i++){ // 1 次
println(i); // n 次
}
先别管这个算法有什么用,我们来看 f(n)=n+2, T(n) = O(n+2) = O(n)
所以这个算法的时间复杂度为 O(n), 要具体学习怎么表达时间复杂度可以自己找其他书籍学习。
常见实际复杂度:
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
其他还有 最坏/最好/平均时间复杂度 的概念,一个算法通常花费的时间复杂度不同,我们来具体实际例子吧。
假设你上次交的作业 发下来了,现在要在 n 本书中找到你的那本书。 问题规模就是 n。
假设我们使用这种算法:(遍历)一本一本的查。那测试数据就是 1。
最好的情况就是第一本就找到了,那么执行语句就是 1, 时间复杂度就是 O(1),这就是最好时间复杂度。
最坏的情况就是最后一本才是,那么执行语句就是 n,时间复杂度就是 O(n) ,这就是最坏时间复杂度。
平均的情况要复杂些,这里就不说了。
我们从计算机的目的讲了 data 的发展,然后引出了数据结构,之后我们从又计算机的目的出发,引入了算法的一些概念。
原文:https://www.cnblogs.com/just-save/p/13127220.html