A:http://codeforces.com/contest/1364/problem/A
题意:
n个数的序列,给出x
找出最长的子序列(删除首尾得到的序列),使得和不能被x整除。
解析:
如果总的sum%x!=0,直接输出n
整除段-不能整除段=不能整除段
找到离左端点最近的不能整除x的下标L,离右端点最近的不能整除x的下标R
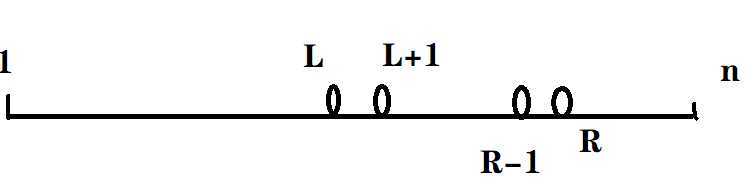
那么1->L,为一个不整除段,L+1->n也是一个不能整除段,R-1同理
所以L+1~n和R-1~1,取个max即可。
#include<iostream> #include<cstring> using namespace std; typedef long long ll; const int maxn=1e5+10; int a[maxn],b[maxn]; int main() { int t; cin>>t; while(t--) { int n,x; cin>>n>>x; ll sum=0; int ok = 0 ; for(int i=1;i<=n;i++) { cin>>a[i]; sum+=a[i]; if(a[i]%x!=0) ok=1; } if(sum%x!=0) { cout<<n<<endl;continue; } if(!ok) { cout<<"-1"<<endl;continue; } int l=1,r=n; for(int i=1;i<=n;i++) if(a[i]%x!=0) { l=i;break; } for(int i=n;i>=1;i--) if(a[i]%x!=0) { r=i;break; } cout<<max(n-l,r-1)<<endl; } return 0; }
B:http://codeforces.com/contest/1364/problem/B
题意:
给出长度为n的序列,找到子序列(通过删除某些元素),使得相邻差值的绝对值之和为最大,在这些最大值之中,找到最短的子序列。
解析:
对于一段递增的序列来说:a1,a2,a3....ai,那么它们的相邻差值之和为ai-a1,中间的可以忽略,因为我们要子序列尽可能短
对于一段递减的序列来说:ai....a1,相邻差值之和为ai-a1,中间的也是可以忽略。
很明显,如果让差值之和尽可能大,需要子序列增减性交替进行。
所以,找到所有的峰点和低谷点,即为答案。
#include<iostream> #include<cstring> using namespace std; typedef long long ll; const int maxn=1e5+10; int a[maxn],b[maxn]; int main() { int t; cin>>t; while(t--) { int n; cin>>n; for(int i=1;i<=n;i++) cin>>a[i]; b[1]=1; int tot=2; for(int i=2;i<n;i++) { if(a[i]>a[i-1]&&a[i]>a[i+1]||a[i]<a[i-1]&&a[i]<a[i+1]) b[tot++]=i; } b[tot]=n; cout<<tot<<endl; for(int i=1;i<=tot;i++) cout<<a[b[i]]<<" "; cout<<endl; } return 0; }
C:http://codeforces.com/contest/1364/problem/C
题意:
给出长度为n的a[],求b[],使得MEX{b1....bi}=ai,即为b[1]~b[i]中未出现的数中的最小值。
解析:
由于条件的限制:序列非递减,ai<=i,所以一定有解。
由于ai<=i,所以第一位:a1==1||a1==0,所以我们从这里入手。
假如a1==1,那么b[1]一定为0,假设a[]:1,1,1,1,1,1........2,3,4
在连续1中,一直加入a[]未出现的数字,每一个1,都满足:在b1~bi中未出现,而且是最小。所以可以看出,对于a[i]==a[i-1],依次加入未出现的数,是一定可以满足条件的。
对于a[i]!=a[i-1],由于a[i-1]已经满足条件了,而且ai<=i,所以b[i]==a[i-1]
#include<iostream> #include<cstring> using namespace std; typedef long long ll; const int maxn=1e5+10; int a[maxn],v[maxn]; int main() { int n; // memset(v,0,sizeof(v)); cin>>n; for(int i=1;i<=n;i++) { cin>>a[i]; v[a[i]]=1; } int tot=0; for(int i=1;i<=n;i++) { if(a[i]!=a[i-1]&&i!=1) cout<<a[i-1]<<" "; else { while(v[tot]==1) { tot++; } cout<<tot<<" "; tot++; } } }
Codeforces Round #649 (Div. 2)ABC
原文:https://www.cnblogs.com/liyexin/p/13127432.html