一句话概述:GloVe是一种基于全局语料计数的无监督学习模型,但是采用log(X)作为label,故损失函数采用最小平方损失函数。从全局考虑输出词向量表征。
它来自斯坦福的一篇论文,GloVe全称应该是?Global?Vectors for Word Representation,它是一个基于全局词频统计(count-based & overall statistics)的词表征(word representation)工具。它可以把一个单词表达成一个由实数组成的向量,这些向量捕捉到了单词之间一些语义特性,比如相似性(similarity)、类比性(analogy)等。我们通过对向量的运算,比如欧几里得距离或者cosine相似度,可以计算出两个单词之间的语义相似性。
模型目标:进行词的向量化表示,使得向量之间尽可能多地蕴含语义和语法的信息。
输入:语料库
输出:词向量
方法概述:首先基于语料库构建词的共现矩阵,然后基于共现矩阵和GloVe模型学习词向量。
** 开始 -> 统计共现矩阵 -> 训练词向量 -> 结束**
1)根据语料库(corpus)构建一个共现矩阵(Co-ocurrence Matrix)X
矩阵中的每一个元素Xij代表单词i和上下文单词j在特定大小的上下文窗口(context window)内共同出现的次数。一般而言,这个次数的最小单位是1,但是GloVe不这么认为:它根据两个单词在上下文窗口的距离d,提出了一个衰减函数(decreasing weighting):decay=1/d 用于计算权重,也就是说距离越远的两个单词所占总计数(total count)的权重越小。
2)构建词向量(Word Vector)和共现矩阵(Co-ocurrence Matrix)之间的近似关系
论文的作者提出以下的公式可以近似地表达两者之间的关系:
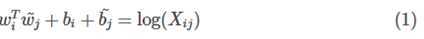
其中,是我们最终要求解的词向量;分别是两个词向量的bias term。公式的由来见下文的第三节。
3)根据loss function求解
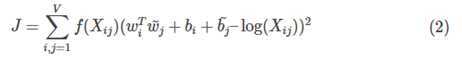
这个loss function的基本形式就是最简单的mean square loss,只不过在此基础上加了一个权重函数,其作用如下:
1、非递减函数的属性(non-decreasing)
2、防止权重过大(overweighted),当到达一定程度之后应该不再增加
3、当两个单词没有同时出现时,,那么他们应该不参与到loss function的计算当中去,即
满足以上两个条件的函数有很多,作者采用了如下形式的分段函数:
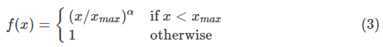
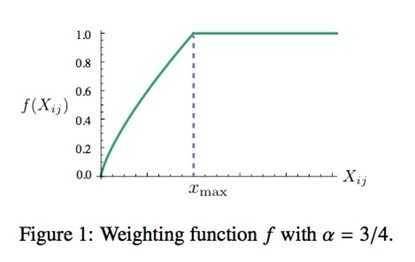
这篇论文中的所有实验,α的取值都是0.75,而取值都是100。这个函数图像如下所示:
虽然很多人声称GloVe是一种无监督(unsupervised learing)的学习方式(因为它确实不需要人工标注label),但其实它还是有label的,只是来源于本身,这个label就是公式2中的 ,而公式2中的向量 w 和 就是要不断更新/学习的参数,本质上它的训练方式跟监督学习的训练方法没什么不一样,都是基于梯度下降的。具体地,这篇论文里的实验是这么做的:采用了AdaGrad的梯度下降算法,对矩阵X中的所有非零元素进行随机采样,学习曲率(learning rate)设为0.05,在vector size小于300的情况下迭代了50次,其他大小的vectors上迭代了100次,直至收敛。最终学习得到的是两个vector是 w 和 ,因为X是对称的(symmetric),所以从原理上讲w和~w是也是对称的,他们唯一的区别是初始化的值不一样,而导致最终的值不一样。所以这两者其实是等价的,都可以当成最终的结果来使用。但是为了提高鲁棒性,我们最终会选择两者之和 w 和 作为最终的vector(两者的初始化不同相当于加了不同的随机噪声,所以能提高鲁棒性)。在训练了400亿个token组成的语料后,得到的实验结果如下图所示:
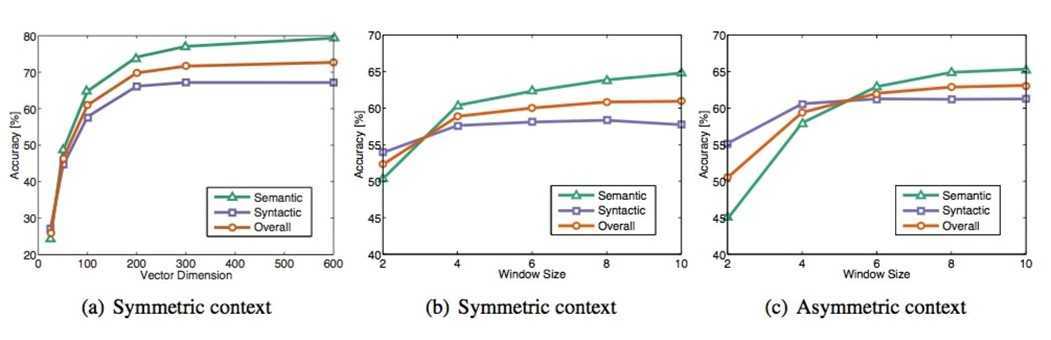
这个图一共采用了三个指标:语义准确度,语法准确度以及总体准确度。那么我们不难发现Vector Dimension在300时能达到最佳,而context Windows size大致在6到10之间。
不感兴趣可以跳过,不影响理解整体思路。
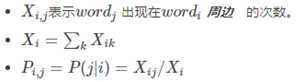
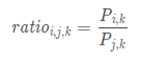
ratioi,j,k?的值 | 单词j,k相关 | 单词j,k不相关 |
单词i,k相关 | 趋近1 | 很大 |
单词i,k不相关 | 很小 | 趋近1 |
通过上表格,很容易发现我们词向量与共现矩阵具有很好的一致性,也就说明我们的词向量中蕴含了共现矩阵中所蕴含的信息。论文中给了更加直观的理解:
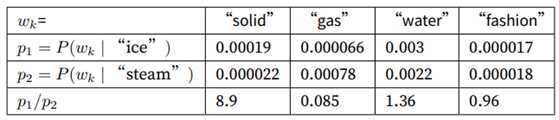

我们是否可以model 出一个模型,能很好的反映上述关系?假设我们找到了这样的一个模型F:

这里面w表示的是一个词向量, ?表示其在 context_windows内的某个词。显然我们希望这个F能表示上述比率的关系。因为向量空间是线性的,因此我们可以将函数?F改变为:

这时我们发现公式5的右侧是一个数量,而左侧则是一个向量,于是我们把左侧转换成两个向量的内积形式:

论文中进行如下变换(w 和 的角色等价,互换后得出,不知可对,存疑)
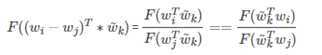
展开前面:
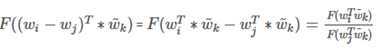
显然exp 函数具有这个特性,也就是F为exp函数,再结合(6)分子和分母对应相等得到:
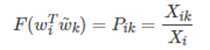
对上式去对数得道:
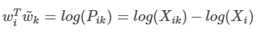
可推到出:
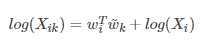
我们可以把纳入到的偏执项中,为了对称性,也加入?的偏置项,则得如下公式:
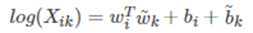
以上模型存在一个问题:他将共现矩阵中每个元素的权重都视作一样,这是不合理的,例如,一个很少出现的词汇携带的信息要比频繁出现的词汇携带的信息要少得多,顾前面加上f(x)权重函数。
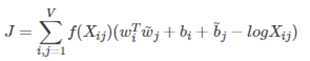
1)glove vs LSA
LSA(Latent Semantic Analysis)可以基于co-occurance matrix构建词向量,实质上是基于全局语料采用SVD进行矩阵分解,然而SVD计算复杂度高;
glove可看作是对LSA一种优化的高效矩阵分解算法,采用Adagrad对最小平方损失进行优化;
2)word2vec vs glove
【1】论文:?http://nlp.stanford.edu/projects/glove/ https://www.aclweb.org/anthology/D14-1162/
【2】官方的代码的GitHub :?https://github.com/stanfordnlp/GloVe
【3】其它代码研究:
https://blog.csdn.net/weixin_36711901/article/details/78508798
https://github.com/stanfordnlp/GloVe/tree/master/src
https://zhuanlan.zhihu.com/p/28613493
https://github.com/maciejkula/glove-python
【4】GloVe详解 : http://www.fanyeong.com/2018/02/19/glove-in-detail/#comment-1462
【NLP-07】GloVe(Global?Vectors for Word Representation)
原文:https://www.cnblogs.com/yifanrensheng/p/13149458.html