转自：http://www.gwylab.com/note-vae.html，这个讲的不错。
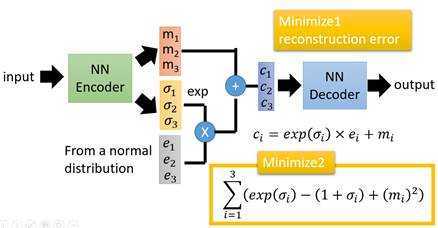
损失函数方面，除了必要的重构损失外，VAE还增添了一个损失函数（见上图Minimize2内容），这同样是必要的部分，因为如果不加的话，
整个模型就会出现问题：为了保证生成图片的质量越高，编码器肯定希望噪音对自身生成图片的干扰越小，于是分配给噪音的权重越小，这样只需要将(
)赋为接近负无穷大的值就好了。（那么在ci中，第一项就为0了，就退化为了自编码器。）
所以，第二个损失函数就有限制编码器走这样极端路径的作用（如果此时再赋值为负无穷大，那么第二项就为正无穷大，但是总体是要minimize它的，所以不会使得σ负无穷大了），这也从直观上就能看出来，exp(
)-(1+)在=0处取得最小值（但是σ实际上不会是0的），于是()就会避免被赋值为负无穷大。
对于生成模型而言，主流的理论模型可以分为隐马尔可夫模型HMM、朴素贝叶斯模型NB和高斯混合模型GMM，而VAE的理论基础就是高斯混合模型。
什么是高斯混合模型呢？就是说，任何一个数据的分布，都可以看作是若干高斯分布的叠加。
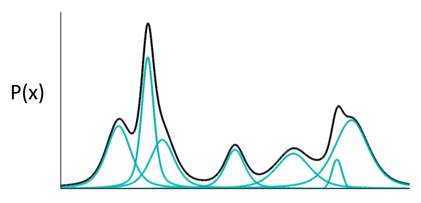
如果P(X)代表一种分布的话，存在一种拆分方法能让它表示成图中若干浅蓝色曲线对应的高斯分布的叠加。有意思的是，这种拆分方法已经证明出，当拆分的数量达到512时，其叠加的分布相对于原始分布而言，误差是非常非常小的了。
那么对于离散值来说：
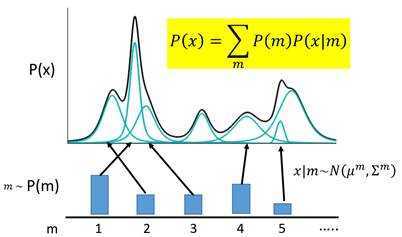
m代表着编码维度上的编号，譬如实现一个512维的编码，m的取值范围就是1,2,3……512。m会服从于一个概率分布P(m)（多项式分布）。
m表示每一个样本属于一个高斯分布的概率吧，m也服从一个上述的多项式的概率分布，那么总的px就可以表示为这些分布的叠加。
现在编码的对应关系是，每采样一个m，其对应到一个小的高斯分布
，P(X)就可以等价为所有的这些高斯分布的叠加，即上图中黄色部分。
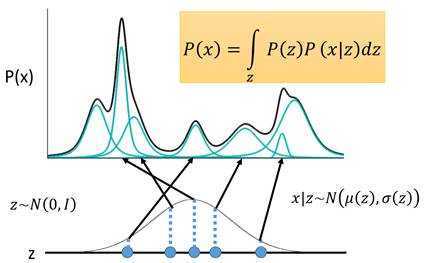
那么这个是针对连续的，z相当于m，z不是多项式分布，而是一个高斯分布。那么求和变为了求积分。
https://zhuanlan.zhihu.com/p/68903857，讲了个大概，可以看看。
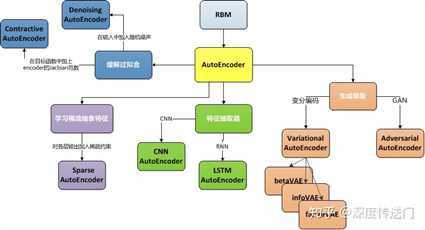
//原来有这么多的变形啊！
原文：https://www.cnblogs.com/BlueBlueSea/p/13149464.html