隐马尔科夫HMM模型是一类重要的机器学习方法,其主要用于序列数据的分析,广泛应用于语音识别、文本翻译、序列预测、中文分词等多个领域。虽然近年来,由于RNN等深度学习方法的发展,HMM模型逐渐变得不怎么流行了,但并不意味着完全退出应用领域,甚至在一些轻量级的任务中仍有应用。本系列博客将详细剖析隐马尔科夫链HMM模型,同以往网络上绝大多数教程不同,本系列博客将更深入地分析HMM,不仅包括估计序列隐状态的维特比算法(HMM解码问题)、前向后向算法等,而且还着重的分析HMM的EM训练过程,并将所有的过程都通过数学公式进行推导。
由于隐马尔科夫HMM模型是一类非常复杂的模型,其中包含了大量概率统计的数学知识,因此网络上多数博客一般都采用举例等比较通俗的方式来介绍HMM,这么做会让初学者很快明白HMM的原理,但要丢失了大量细节,让初学者处于一种似懂非懂的状态。而本文并没有考虑用非常通俗的文字描述HMM,还是考虑通过详细的数学公式来一步步引导初学者掌握HMM的思想。另外,本文重点分析了HMM的EM训练过程,这是网络上其他教程所没有的,而个人认为相比于维特比算法、前向后向算法,HMM的EM训练过程虽然更为复杂,但是一旦掌握这个训练过程,那么对于通用的链状图结构的推导、EM算法和网络训练的理解都会非常大的帮助。另外通过总结HMM的数学原理,也能非常方便将数学公式改写成代码。
最后,本文提供了一个简单版本的隐马尔科夫链HMM的Python代码,包含了高斯模型的HMM和离散HMM两种情况,代码中包含了HMM的训练、预测、解码等全部过程,核心代码总共只有200~300行代码。
觉得好,就点星哦!
觉得好,就点星哦!
觉得好,就点星哦!
重要的事要说三遍!!!!
为了方便大家学习,我将整个HMM代码完善成整个学习项目,其中包括
hmm.py:HMM核心代码,包含了一个HMM基类,一个高斯HMM模型及一个离散HMM模型
DiscreteHMM_test.py及GaussianHMM_test.py:利用unnitest来测试我们的HMM,同时引入了一个经典HMM库hmmlearn作为对照组
Dice_01.py:利用离散HMM模型来解决丢色子问题的例子
Wordseg_02.py:解决中文分词问题的例子
Stock_03.py:解决股票预测问题的例子
首先,已知一组序列 :
我们从这组序列中推导出产生这组序列的函数,假设函数参数为 ,其表示为
即使得序列X发生概率最大的函数参数,要解决上式,最简单的考虑是将序列 的每个数据都视为独立的,比如建立一个神经网络。然后这种考虑会随着序列增长,而导致参数爆炸式增长。因此可以假设当前序列数据只与其前一数据值相关,即所谓的一阶马尔科夫链:
有一阶马尔科夫链,也会有二阶马尔科夫链(即当前数据值取决于其前两个数据值)
当前本文不对二阶马尔科夫链进行深入分析了,着重考虑一阶马尔科夫链,现在根据一阶马尔科夫链的假设,我们有:
因此要解一阶马尔科夫链,其关键在于求数据(以下称观测值)之间转换函数 ,如果假设转换函数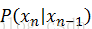
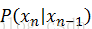
然而,如果观测值x的状态非常多(特别极端的情况是连续数据),转换函数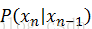
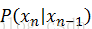
为了降低马尔科夫链的转换函数的参数量,我们引入了一个包含较少状态的隐状态值,将观测值的马尔科夫链转换为隐状态的马尔科夫链(即为隐马尔科夫链HMM)
其包含了一个重要假设:当前观测值只由当前隐状态所决定。这么做的一个重要好处是,隐状态值的状态远小于观测值的状态,因此隐藏状态的转换函数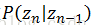
此时我们要决定的问题是:
即在所有可能隐藏状态序列情况下,求使得序列 发生概率最大的函数参数 。
这里我们再总结下:
1. 当前观测值只由当前隐藏状态确定,而与其他隐藏状态或观测值无关(隐藏状态假设)
2. 当前隐藏状态由其前一个隐藏状态决定(一阶马尔科夫假设)
3. 隐藏状态之间的转换函数概率不随时间变化(转换函数稳定性假设)
在所有可能隐藏状态序列情况下,求使得当前序列X产生概率最大的函数参数θ。
# -*- coding:utf-8 -*- # 隐马尔科夫链模型 from abc import ABCMeta, abstractmethod import numpy as np from math import pi, sqrt, exp, pow from numpy.linalg import det, inv from sklearn import cluster class _BaseHMM(): """ 基本HMM虚类,需要重写关于发射概率的相关虚函数 n_state : 隐藏状态的数目 n_iter : 迭代次数 x_size : 观测值维度 start_prob : 初始概率 transmat_prob : 状态转换概率 """ __metaclass__ = ABCMeta # 虚类声明 def __init__(self, n_state=1, x_size=1, iter=20): self.n_state = n_state self.x_size = x_size self.start_prob = np.ones(n_state) * (1.0 / n_state) # 初始状态概率 self.transmat_prob = np.ones((n_state, n_state)) * (1.0 / n_state) # 状态转换概率矩阵 self.trained = False # 是否需要重新训练 self.n_iter = iter # EM训练的迭代次数 # 初始化发射参数 @abstractmethod def _init(self, X): pass # 虚函数:返回发射概率 @abstractmethod def emit_prob(self, x): # 求x在状态k下的发射概率 P(X|Z) return np.array([0]) # 虚函数 @abstractmethod def generate_x(self, z): # 根据隐状态生成观测值x p(x|z) return np.array([0]) # 虚函数:发射概率的更新 @abstractmethod def emit_prob_updated(self, X, post_state): pass # 通过HMM生成序列 def generate_seq(self, seq_length): X = np.zeros((seq_length, self.x_size)) Z = np.zeros(seq_length) Z_pre = np.random.choice(self.n_state, 1, p=self.start_prob) # 采样初始状态 X[0] = self.generate_x(Z_pre) # 采样得到序列第一个值 Z[0] = Z_pre for i in range(seq_length): if i == 0: continue # P(Zn+1)=P(Zn+1|Zn)P(Zn) Z_next = np.random.choice(self.n_state, 1, p=self.transmat_prob[Z_pre, :][0]) Z_pre = Z_next # P(Xn+1|Zn+1) X[i] = self.generate_x(Z_pre) Z[i] = Z_pre return X, Z # 估计序列X出现的概率 def X_prob(self, X, Z_seq=np.array([])): # 状态序列预处理 # 判断是否已知隐藏状态 X_length = len(X) if Z_seq.any(): Z = np.zeros((X_length, self.n_state)) for i in range(X_length): Z[i][int(Z_seq[i])] = 1 else: Z = np.ones((X_length, self.n_state)) # 向前向后传递因子 _, c = self.forward(X, Z) # P(x,z) # 序列的出现概率估计 prob_X = np.sum(np.log(c)) # P(X) return prob_X # 已知当前序列预测未来(下一个)观测值的概率 def predict(self, X, x_next, Z_seq=np.array([]), istrain=True): if self.trained == False or istrain == False: # 需要根据该序列重新训练 self.train(X) X_length = len(X) if Z_seq.any(): Z = np.zeros((X_length, self.n_state)) for i in range(X_length): Z[i][int(Z_seq[i])] = 1 else: Z = np.ones((X_length, self.n_state)) # 向前向后传递因子 alpha, _ = self.forward(X, Z) # P(x,z) prob_x_next = self.emit_prob(np.array([x_next])) * np.dot(alpha[X_length - 1], self.transmat_prob) return prob_x_next def decode(self, X, istrain=True): """ 利用维特比算法,已知序列求其隐藏状态值 :param X: 观测值序列 :param istrain: 是否根据该序列进行训练 :return: 隐藏状态序列 """ if self.trained == False or istrain == False: # 需要根据该序列重新训练 self.train(X) X_length = len(X) # 序列长度 state = np.zeros(X_length) # 隐藏状态 pre_state = np.zeros((X_length, self.n_state)) # 保存转换到当前隐藏状态的最可能的前一状态 max_pro_state = np.zeros((X_length, self.n_state)) # 保存传递到序列某位置当前状态的最大概率 _, c = self.forward(X, np.ones((X_length, self.n_state))) max_pro_state[0] = self.emit_prob(X[0]) * self.start_prob * (1 / c[0]) # 初始概率 # 前向过程 for i in range(X_length): if i == 0: continue for k in range(self.n_state): prob_state = self.emit_prob(X[i])[k] * self.transmat_prob[:, k] * max_pro_state[i - 1] max_pro_state[i][k] = np.max(prob_state) * (1 / c[i]) pre_state[i][k] = np.argmax(prob_state) # 后向过程 state[X_length - 1] = np.argmax(max_pro_state[X_length - 1, :]) for i in reversed(range(X_length)): if i == X_length - 1: continue state[i] = pre_state[i + 1][int(state[i + 1])] return state # 针对于多个序列的训练问题 def train_batch(self, X, Z_seq=list()): # 针对于多个序列的训练问题,其实最简单的方法是将多个序列合并成一个序列,而唯一需要调整的是初始状态概率 # 输入X类型:list(array),数组链表的形式 # 输入Z类型: list(array),数组链表的形式,默认为空列表(即未知隐状态情况) self.trained = True X_num = len(X) # 序列个数 self._init(self.expand_list(X)) # 发射概率的初始化 # 状态序列预处理,将单个状态转换为1-to-k的形式 # 判断是否已知隐藏状态 if Z_seq == list(): Z = [] # 初始化状态序列list for n in range(X_num): Z.append(list(np.ones((len(X[n]), self.n_state)))) else: Z = [] for n in range(X_num): Z.append(np.zeros((len(X[n]), self.n_state))) for i in range(len(Z[n])): Z[n][i][int(Z_seq[n][i])] = 1 for e in range(self.n_iter): # EM步骤迭代 # 更新初始概率过程 # E步骤 print("iter: ", e) b_post_state = [] # 批量累积:状态的后验概率,类型list(array) b_post_adj_state = np.zeros((self.n_state, self.n_state)) # 批量累积:相邻状态的联合后验概率,数组 b_start_prob = np.zeros(self.n_state) # 批量累积初始概率 for n in range(X_num): # 对于每个序列的处理 X_length = len(X[n]) alpha, c = self.forward(X[n], Z[n]) # P(x,z) beta = self.backward(X[n], Z[n], c) # P(x|z) post_state = alpha * beta / np.sum(alpha * beta) # 归一化! b_post_state.append(post_state) post_adj_state = np.zeros((self.n_state, self.n_state)) # 相邻状态的联合后验概率 for i in range(X_length): if i == 0: continue if c[i] == 0: continue post_adj_state += (1 / c[i]) * np.outer(alpha[i - 1], beta[i] * self.emit_prob(X[n][i])) * self.transmat_prob if np.sum(post_adj_state) != 0: post_adj_state = post_adj_state / np.sum(post_adj_state) # 归一化! b_post_adj_state += post_adj_state # 批量累积:状态的后验概率 b_start_prob += b_post_state[n][0] # 批量累积初始概率 # M步骤,估计参数,最好不要让初始概率都为0出现,这会导致alpha也为0 b_start_prob += 0.001 * np.ones(self.n_state) self.start_prob = b_start_prob / np.sum(b_start_prob) b_post_adj_state += 0.001 for k in range(self.n_state): if np.sum(b_post_adj_state[k]) == 0: continue self.transmat_prob[k] = b_post_adj_state[k] / np.sum(b_post_adj_state[k]) self.emit_prob_updated(self.expand_list(X), self.expand_list(b_post_state)) def expand_list(self, X): # 将list(array)类型的数据展开成array类型 C = [] for i in range(len(X)): C += list(X[i]) return np.array(C) # 针对于单个长序列的训练 def train(self, X, Z_seq=np.array([])): # 输入X类型:array,数组的形式 # 输入Z类型: array,一维数组的形式,默认为空列表(即未知隐状态情况) self.trained = True X_length = len(X) self._init(X) # 状态序列预处理 # 判断是否已知隐藏状态 if Z_seq.any(): Z = np.zeros((X_length, self.n_state)) for i in range(X_length): Z[i][int(Z_seq[i])] = 1 else: Z = np.ones((X_length, self.n_state)) for e in range(self.n_iter): # EM步骤迭代 # 中间参数 print(e, " iter") # E步骤 # 向前向后传递因子 alpha, c = self.forward(X, Z) # P(x,z) beta = self.backward(X, Z, c) # P(x|z) post_state = alpha * beta post_adj_state = np.zeros((self.n_state, self.n_state)) # 相邻状态的联合后验概率 for i in range(X_length): if i == 0: continue if c[i] == 0: continue post_adj_state += (1 / c[i]) * np.outer(alpha[i - 1], beta[i] * self.emit_prob(X[i])) * self.transmat_prob # M步骤,估计参数 self.start_prob = post_state[0] / np.sum(post_state[0]) for k in range(self.n_state): self.transmat_prob[k] = post_adj_state[k] / np.sum(post_adj_state[k]) self.emit_prob_updated(X, post_state) # 求向前传递因子 def forward(self, X, Z): X_length = len(X) alpha = np.zeros((X_length, self.n_state)) # P(x,z) alpha[0] = self.emit_prob(X[0]) * self.start_prob * Z[0] # 初始值 # 归一化因子 c = np.zeros(X_length) c[0] = np.sum(alpha[0]) alpha[0] = alpha[0] / c[0] # 递归传递 for i in range(X_length): if i == 0: continue alpha[i] = self.emit_prob(X[i]) * np.dot(alpha[i - 1], self.transmat_prob) * Z[i] c[i] = np.sum(alpha[i]) if c[i] == 0: continue alpha[i] = alpha[i] / c[i] return alpha, c # 求向后传递因子 def backward(self, X, Z, c): X_length = len(X) beta = np.zeros((X_length, self.n_state)) # P(x|z) beta[X_length - 1] = np.ones((self.n_state)) # 递归传递 for i in reversed(range(X_length)): if i == X_length - 1: continue beta[i] = np.dot(beta[i + 1] * self.emit_prob(X[i + 1]), self.transmat_prob.T) * Z[i] if c[i + 1] == 0: continue beta[i] = beta[i] / c[i + 1] return beta # 二元高斯分布函数 def gauss2D(x, mean, cov): # x, mean, cov均为numpy.array类型 z = -np.dot(np.dot((x - mean).T, inv(cov)), (x - mean)) / 2.0 temp = pow(sqrt(2.0 * pi), len(x)) * sqrt(det(cov)) return (1.0 / temp) * exp(z) class GaussianHMM(_BaseHMM): """ 发射概率为高斯分布的HMM 参数: emit_means: 高斯发射概率的均值 emit_covars: 高斯发射概率的方差 """ def __init__(self, n_state=1, x_size=1, iter=20): _BaseHMM.__init__(self, n_state=n_state, x_size=x_size, iter=iter) self.emit_means = np.zeros((n_state, x_size)) # 高斯分布的发射概率均值 self.emit_covars = np.zeros((n_state, x_size, x_size)) # 高斯分布的发射概率协方差 for i in range(n_state): self.emit_covars[i] = np.eye(x_size) # 初始化为均值为0,方差为1的高斯分布函数 def _init(self, X): # 通过K均值聚类,确定状态初始值 mean_kmeans = cluster.KMeans(n_clusters=self.n_state) mean_kmeans.fit(X) self.emit_means = mean_kmeans.cluster_centers_ for i in range(self.n_state): self.emit_covars[i] = np.cov(X.T) + 0.01 * np.eye(len(X[0])) def emit_prob(self, x): # 求x在状态k下的发射概率 prob = np.zeros((self.n_state)) for i in range(self.n_state): prob[i] = gauss2D(x, self.emit_means[i], self.emit_covars[i]) return prob def generate_x(self, z): # 根据状态生成x p(x|z) return np.random.multivariate_normal(self.emit_means[z][0], self.emit_covars[z][0], 1) def emit_prob_updated(self, X, post_state): # 更新发射概率 for k in range(self.n_state): for j in range(self.x_size): self.emit_means[k][j] = np.sum(post_state[:, k] * X[:, j]) / np.sum(post_state[:, k]) X_cov = np.dot((X - self.emit_means[k]).T, (post_state[:, k] * (X - self.emit_means[k]).T).T) self.emit_covars[k] = X_cov / np.sum(post_state[:, k]) if det(self.emit_covars[k]) == 0: # 对奇异矩阵的处理 self.emit_covars[k] = self.emit_covars[k] + 0.01 * np.eye(len(X[0])) class DiscreteHMM(_BaseHMM): """ 发射概率为离散分布的HMM 参数: emit_prob : 离散概率分布 x_num:表示观测值的种类 此时观测值大小x_size默认为1 """ def __init__(self, n_state=1, x_num=1, iter=20): _BaseHMM.__init__(self, n_state=n_state, x_size=1, iter=iter) self.emission_prob = np.ones((n_state, x_num)) * (1.0 / x_num) # 初始化发射概率均值 self.x_num = x_num def _init(self, X): self.emission_prob = np.random.random(size=(self.n_state, self.x_num)) for k in range(self.n_state): self.emission_prob[k] = self.emission_prob[k] / np.sum(self.emission_prob[k]) def emit_prob(self, x): # 求x在状态k下的发射概率 prob = np.zeros(self.n_state) for i in range(self.n_state): prob[i] = self.emission_prob[i][int(x[0])] return prob def generate_x(self, z): # 根据状态生成x p(x|z) return np.random.choice(self.x_num, 1, p=self.emission_prob[z][0]) def emit_prob_updated(self, X, post_state): # 更新发射概率 self.emission_prob = np.zeros((self.n_state, self.x_num)) X_length = len(X) for n in range(X_length): self.emission_prob[:, int(X[n])] += post_state[n] self.emission_prob += 0.1 / self.x_num for k in range(self.n_state): if np.sum(post_state[:, k]) == 0: continue self.emission_prob[k] = self.emission_prob[k] / np.sum(post_state[:, k])
from hmmlearn.hmm import MultinomialHMM import numpy as np import ArtificialIntelligence.hmm as hmm dice_num = 3 x_num = 8 dice_hmm = hmm.DiscreteHMM(3, 8) dice_hmm.start_prob = np.ones(3)/3.0 dice_hmm.transmat_prob = np.ones((3,3))/3.0 dice_hmm.emission_prob = np.array([[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0], [1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0], [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]]) # 归一化 dice_hmm.emission_prob = dice_hmm.emission_prob / np.repeat(np.sum(dice_hmm.emission_prob, 1),8).reshape((3,8)) dice_hmm.trained = True X = np.array([[1],[6],[3],[5],[2],[7],[3],[5],[2],[4],[3],[6],[1],[5],[4]]) Z = dice_hmm.decode(X) # 问题A logprob = dice_hmm.X_prob(X) # 问题B # 问题C x_next = np.zeros((x_num,dice_num)) for i in range(x_num): c = np.array([i]) x_next[i] = dice_hmm.predict(X, i) print ("state: ", Z) print ("logprob: ", logprob) print ("prob of x_next: ", x_next)
执行结果:
C:\Anaconda3\python.exe "C:\Program Files\JetBrains\PyCharm 2019.1.1\helpers\pydev\pydevconsole.py" --mode=client --port=65356 import sys; print(‘Python %s on %s‘ % (sys.version, sys.platform)) sys.path.extend([‘C:\\app\\PycharmProjects‘, ‘C:/app/PycharmProjects‘]) Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] Type ‘copyright‘, ‘credits‘ or ‘license‘ for more information IPython 7.12.0 -- An enhanced Interactive Python. Type ‘?‘ for help. PyDev console: using IPython 7.12.0 Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] on win32 runfile(‘C:/app/PycharmProjects/ArtificialIntelligence/Dice_01.py‘, wdir=‘C:/app/PycharmProjects/ArtificialIntelligence‘) state: [1. 2. 1. 0. 1. 2. 1. 0. 1. 0. 1. 2. 1. 0. 0.] logprob: -33.169958671729184 prob of x_next: [[0.05555556 0.08333333 0.04166667] [0.05555556 0.08333333 0.04166667] [0.05555556 0.08333333 0.04166667] [0.05555556 0.08333333 0.04166667] [0.05555556 0. 0.04166667] [0.05555556 0. 0.04166667] [0. 0. 0.04166667] [0. 0. 0.04166667]]
数据:RenMinData.txt_utf8(完整数据在我有道云笔记上)
代码实现:
import numpy as np import ArtificialIntelligence.hmm as hmm from hmmlearn.hmm import MultinomialHMM state_M = 4 word_N = 0 state_list = {‘B‘:0,‘M‘:1,‘E‘:2,‘S‘:3} # 获得某词的分词结果 # 如:(我:S)、(你好:BE)、(恭喜发财:BMME) def getList(input_str): outpout_str = [] if len(input_str) == 1: outpout_str.append(3) elif len(input_str) == 2: outpout_str = [0,2] else: M_num = len(input_str) -2 M_list = [1] * M_num outpout_str.append(0) outpout_str.extend(M_list) outpout_str.append(2) return outpout_str # 预处理词典:RenMinData.txt_utf8 def precess_data(): ifp = open("C:\文档\个人学习资料\Easy_HMM-master\RenMinData.txt_utf8",‘r‘,encoding=‘utf-8‘) line_num = 0 word_dic = {} word_ind = 0 line_seq = [] state_seq = [] # 保存句子的字序列及每个字的状态序列,并完成字典统计 for line in ifp: line_num += 1 if line_num % 10000 == 0: print (line_num) line = line.strip() if not line:continue line = line.encode(‘utf-8‘).decode("utf-8","ignore") word_list = [] for i in range(len(line)): if line[i] == " ":continue word_list.append(line[i]) # 建立单词表 # if not word_dic.has_key(line[i]): if not line[i] in word_dic: word_dic[line[i]] = word_ind word_ind += 1 line_seq.append(word_list) lineArr = line.split(" ") line_state = [] for item in lineArr: line_state += getList(item) state_seq.append(np.array(line_state)) ifp.close() lines = [] for i in range(line_num): lines.append(np.array([[word_dic[x]] for x in line_seq[i]])) return lines,state_seq,word_dic # 将句子转换成字典序号序列 def word_trans(wordline, word_dic): word_inc = [] line = wordline.strip() line = line.decode("utf-8", "ignore") for n in range(len(line)): word_inc.append([word_dic[line[n]]]) return np.array(word_inc) X,Z,word_dic = precess_data() wordseg_hmm = hmm.DiscreteHMM(4,len(word_dic),5) wordseg_hmm.train_batch(X,Z) print ("startprob_prior: ", wordseg_hmm.start_prob) print ("transmit: ", wordseg_hmm.transmat_prob) sentence_1 = "我要回家吃饭" sentence_2 = "中国人民从此站起来了" sentence_3 = "经党中央研究决定" sentence_4 = "江主席发表重要讲话" Z_1 = wordseg_hmm.decode(word_trans(sentence_1,word_dic)) Z_2 = wordseg_hmm.decode(word_trans(sentence_2,word_dic)) Z_3 = wordseg_hmm.decode(word_trans(sentence_3,word_dic)) Z_4 = wordseg_hmm.decode(word_trans(sentence_4,word_dic)) print (u"我要回家吃饭: ", Z_1) print (u"中国人民从此站起来了: ", Z_2) print (u"经党中央研究决定: ", Z_3) print (u"江主席发表重要讲话: ", Z_4)
执行结果:
C:\Anaconda3\python.exe "C:\Program Files\JetBrains\PyCharm 2019.1.1\helpers\pydev\pydevconsole.py" --mode=client --port=60526 import sys; print(‘Python %s on %s‘ % (sys.version, sys.platform)) sys.path.extend([‘C:\\app\\PycharmProjects‘, ‘C:/app/PycharmProjects‘]) Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] Type ‘copyright‘, ‘credits‘ or ‘license‘ for more information IPython 7.12.0 -- An enhanced Interactive Python. Type ‘?‘ for help. PyDev console: using IPython 7.12.0 Python 3.7.6 (default, Jan 8 2020, 20:23:39) [MSC v.1916 64 bit (AMD64)] on win32 runfile(‘C:/app/PycharmProjects/ArtificialIntelligence/test.py‘, wdir=‘C:/app/PycharmProjects/ArtificialIntelligence‘) 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000 110000 120000 130000 140000 150000 160000 170000 180000 190000 200000 210000 220000 230000 240000 250000 260000 270000 280000 290000
pip install https://github.com/matplotlib/mpl_finance/archive/master.zip from mpl_finance import quotes_historical_yahoo
代码实现:
import datetime import numpy as np from matplotlib import cm, pyplot as plt from matplotlib.dates import YearLocator, MonthLocator # from matplotlib.finance import quotes_historical_yahoo_ochl from mpl_finance import quotes_historical_yahoo # from mpl_finance import candlestick_ohlc from ArtificialIntelligence.hmm import GaussianHMM from sklearn.preprocessing import scale ############################################################################### # 导入Yahoo金融数据 quotes = quotes_historical_yahoo( "INTC", datetime.date(1995, 1, 1), datetime.date(2012, 1, 6)) dates = np.array([q[0] for q in quotes], dtype=int) # 日期列 close_v = np.array([q[2] for q in quotes]) # 收盘价 volume = np.array([q[5] for q in quotes])[1:] # 交易数 # diff:out[n] = a[n+1] - a[n] 得到价格变化 diff = np.diff(close_v) dates = dates[1:] close_v = close_v[1:] # scale归一化处理:均值为0和方差为1 # 将价格和交易数组成输入数据 X = np.column_stack([scale(diff), scale(volume)]) # 训练高斯HMM模型,这里假设隐藏状态4个 model = GaussianHMM(4,2,20) model.train(X) # 预测隐状态 hidden_states = model.decode(X) # 打印参数 print("Transition matrix: ", model.transmat_prob) print("Means and vars of each hidden state") for i in range(model.n_state): print("{0}th hidden state".format(i)) print("mean = ", model.emit_means[i]) print("var = ", model.emit_covars[i]) print() # 画图描述 fig, axs = plt.subplots(model.n_state, sharex=True, sharey=True) colours = cm.rainbow(np.linspace(0, 1, model.n_state)) for i, (ax, colour) in enumerate(zip(axs, colours)): # Use fancy indexing to plot data in each state. mask = hidden_states == i ax.plot_date(dates[mask], close_v[mask], ".-", c=colour) ax.set_title("{0}th hidden state".format(i)) # Format the ticks. ax.xaxis.set_major_locator(YearLocator()) ax.xaxis.set_minor_locator(MonthLocator()) ax.grid(True) plt.show()
执行结果:
原文:https://www.cnblogs.com/huanghanyu/p/13156651.html