双链表以类似的方式工作,但还有一个引用字段,称为“prev”字段。有了这个额外的字段,您就能够知道当前结点的前一个结点。
让我们看一个例子:

绿色箭头表示我们的“prev”字段是如何工作的。
下面是双链表中结点结构golang版本的典型定义:
type MyLinkedList struct {
val int
Prev *MyLinkedList
Next *MyLinkedList
}
与单链接列表类似,我们将使用头结点来表示整个列表。
我们可以与单链表相同的方式访问数据:
访问随机位置。O(N),其中 N 是链表的长度。对于添加和删除,会稍微复杂一些,因为我们还需要处理“prev”字段。
如果我们想在现有的结点 prev 之后插入一个新的结点 cur,我们可以将此过程分为两个步骤:
cur 与 prev 和 next,其中 next 是 prev 原始的下一个节点;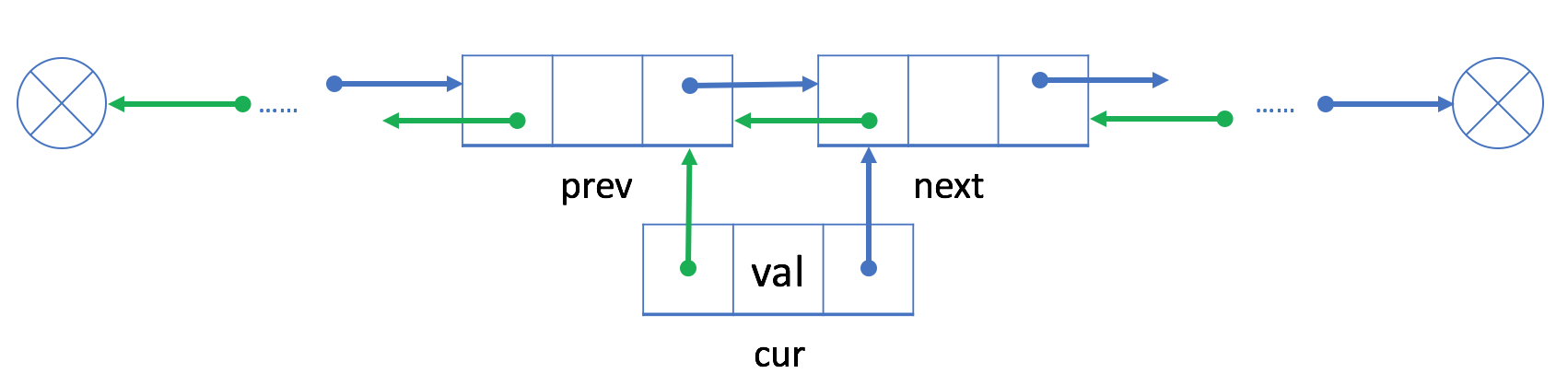
cur 重新链接 prev 和 next。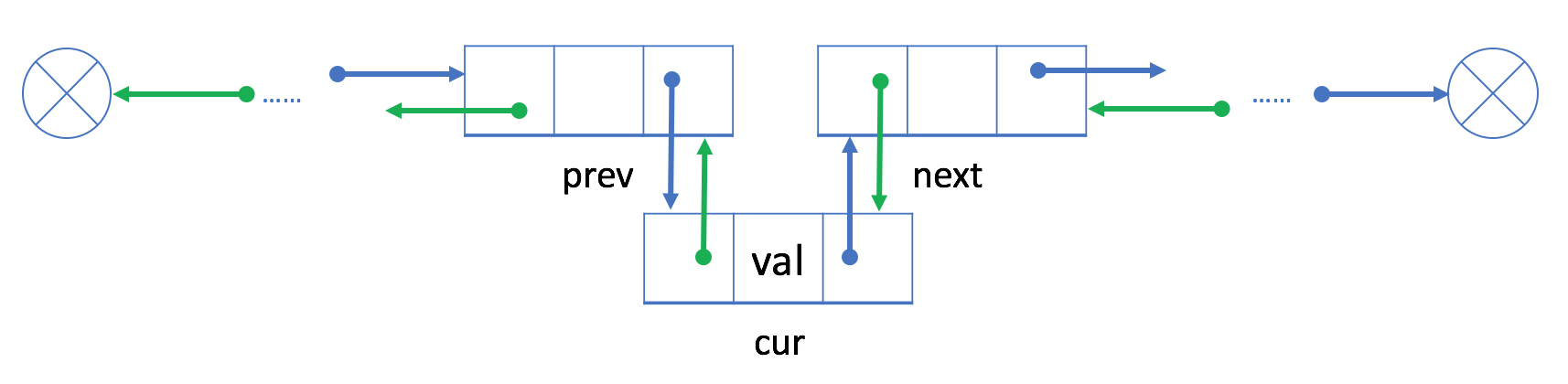
与单链表类似,添加操作的时间和空间复杂度都是 O(1)。

让我们在现有结点 6 之后添加一个新结点 9:
cur(结点 9)与 prev(结点 6)和 next(结点 15)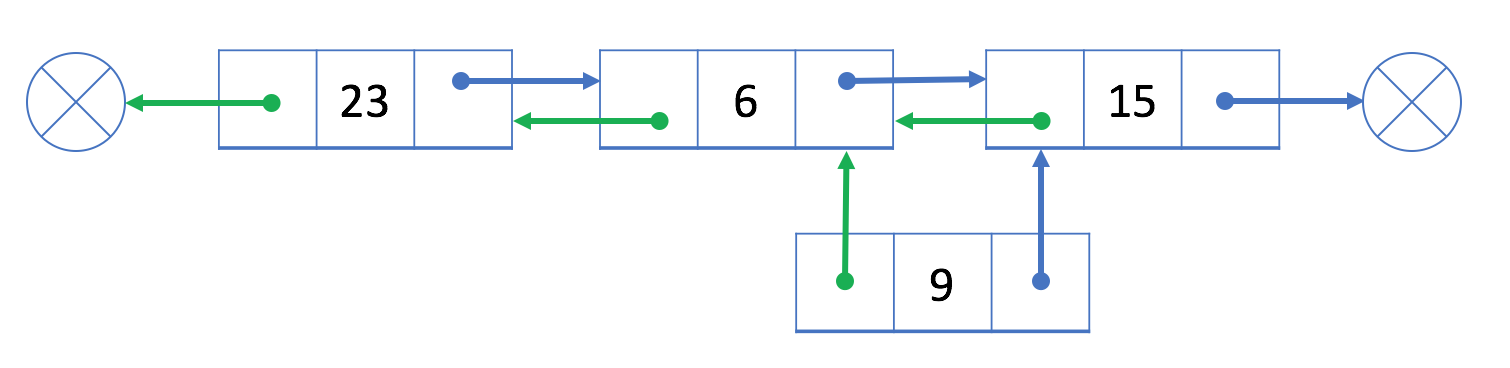
cur(结点 9)重新链接 prev(结点 6)和 next(结点 15)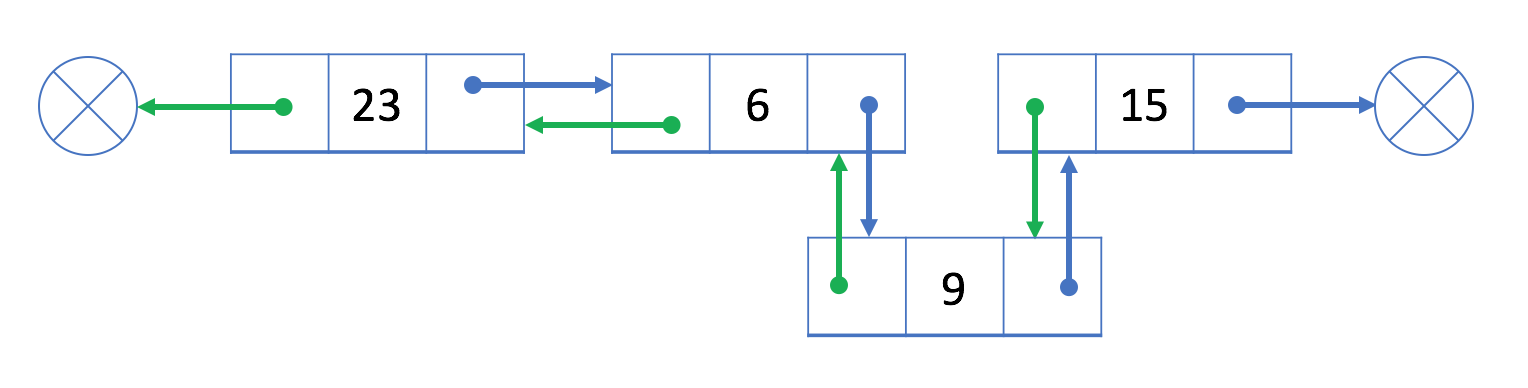
如果我们想从双链表中删除一个现有的结点 cur,我们可以简单地将它的前一个结点 prev 与下一个结点 next 链接起来。
与单链表不同,使用“prev”字段可以很容易地在常量时间内获得前一个结点。
因为我们不再需要遍历链表来获取前一个结点,所以时间和空间复杂度都是O(1)。

我们的目标是从双链表中删除结点 6。
因此,我们将它的前一个结点 23 和下一个结点 15 链接起来:

结点 6 现在不在我们的双链表中。
让我们简要回顾一下单链表和双链表的表现。
它们在许多操作中是相似的。
随机访问数据。在 O(1) 时间内在给定结点之后或列表开头添加一个新结点。在 O(1) 时间内删除第一个结点。但是删除给定结点(包括最后一个结点)时略有不同。
O(N) 时间来找出前一结点。O(1) 时间内删除给定结点。这里我们提供链表和其他数据结构(包括数组,队列和栈)之间时间复杂度的比较:
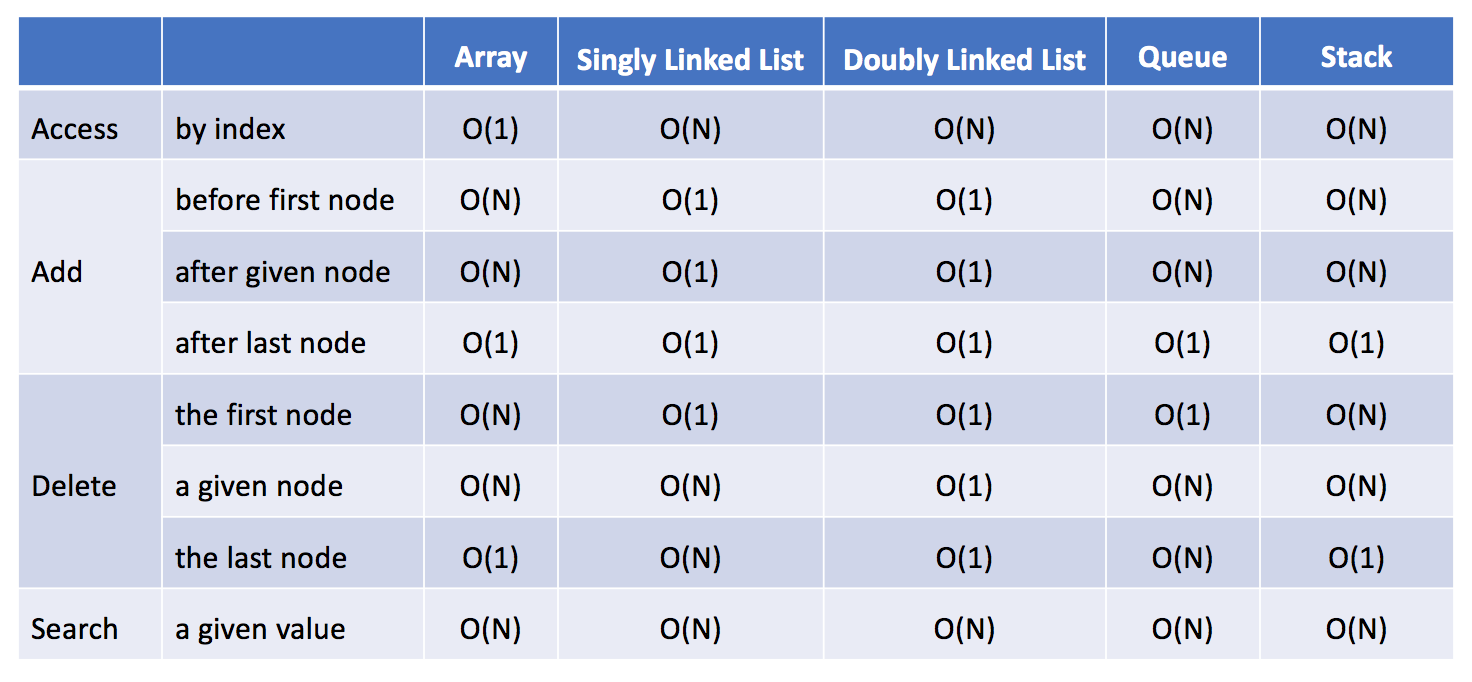
经过这次比较,我们可以结论:
如果你需要经常添加或删除结点,链表可能是一个不错的选择。
如果你需要经常按索引访问元素,数组可能是比链表更好的选择。
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4
解:
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
p := &ListNode{}
result := p // 哨兵节点
for l1 != nil && l2 != nil {
if l1.Val < l2.Val {
p.Next = l1
l1 = l1.Next
} else {
p.Next = l2
l2 = l2.Next
}
p = p.Next
}
// 剩余节点一定是最大的
if l1 != nil {
p.Next = l1
}
if l2 != nil {
p.Next = l2
}
return result.Next
}
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807
解:
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
/*
注意:自己创建的链表,给下一个节点赋值(Val)前,要先分配内存,不能直接赋值。
newNode.Next = new(ListNode)
newNode = newNode.Next
newNodet.Val = XXX
*/
head := &ListNode{} // 新建链表哨兵节点
result := head // 返回链表
count := 0
sum := 0
if l1 == nil && l2 == nil {
return nil
}
for l1 != nil || l2 != nil {
if l1 != nil && l2 == nil {
sum = l1.Val + count
l1 = l1.Next
} else if l1 == nil && l2 != nil {
sum = l2.Val + count
l2 = l2.Next
} else {
sum = l1.Val + l2.Val + count
l1 = l1.Next
l2 = l2.Next
}
// 进位
if sum >= 10 {
count = 1
sum = sum%10
} else {
count = 0
}
head.Next = new(ListNode) // 要记得分配内存
head = head.Next
head.Val = sum
}
// 进位+1
if count == 1 {
head.Next = new(ListNode)
head = head.Next
head.Val = 1
}
return result.Next
}
// 进阶版
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
result := new(ListNode)
curr := result
carry := 0
for l1 != nil || l2 != nil || carry > 0 {
curr.Next = new(ListNode) // 为下一个节点分配内存
curr = curr.Next // 前进!
if l1 != nil {
carry += l1.Val
l1 = l1.Next
}
if l2 != nil {
carry += l2.Val
l2 = l2.Next
}
curr.Val = carry % 10
carry /= 10
}
return result.Next
}
给定一个链表,旋转链表,将链表每个节点向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL
示例 2:
输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL
解:
func rotateRight(head *ListNode, k int) *ListNode {
/*
先遍历求得链表总长度count,同时将链表首尾相连;
再找到原链表的倒数第k+1个节点,即正数第count-k-1个节点,该节点的next就是新链表的头结点。
*/
// 空列表情况、k=0情况
if head == nil || head.Next == nil || k == 0 {
return head
}
// 链表总节点数
count := 1
tmp := head
for tmp.Next != nil {
count++
tmp = tmp.Next
}
k = k % count
// k=0时,不需要旋转
if k == 0 {
return head
}
// 首尾相联
tmp.Next = head
// 找到倒数第k+1个节点,即正数第count-k-1个节点
for i := 0; i < count-k; i++ {
tmp = tmp.Next
}
// 新表头
newHead := tmp.Next
// 链尾---> nil
tmp.Next = nil
return newHead
}
原文:https://www.cnblogs.com/newbase/p/13156980.html