1.雷达设备
题目链接:https://www.acwing.com/problem/content/114/
解决思路:我们所要找到的是雷达的最小数目,因此我们需要对每个小岛进行大都分析
①求出能够到达他的海岸线的范围,通过d与y我们可以求出他的x轴上的覆盖范围,(l,r),然后按照区间的右端点排序。
②求出每个岛的覆盖范围后,我们需要找出最少的使用雷达的数量,如果当前区间包括下一点的区间范围,则直接跳过;如果当前区间不能包含下一个区间,则增加一个雷达数目,并且将雷达范围更新为下一个雷达的区间。
例如下图所示:只需要三个雷达即可
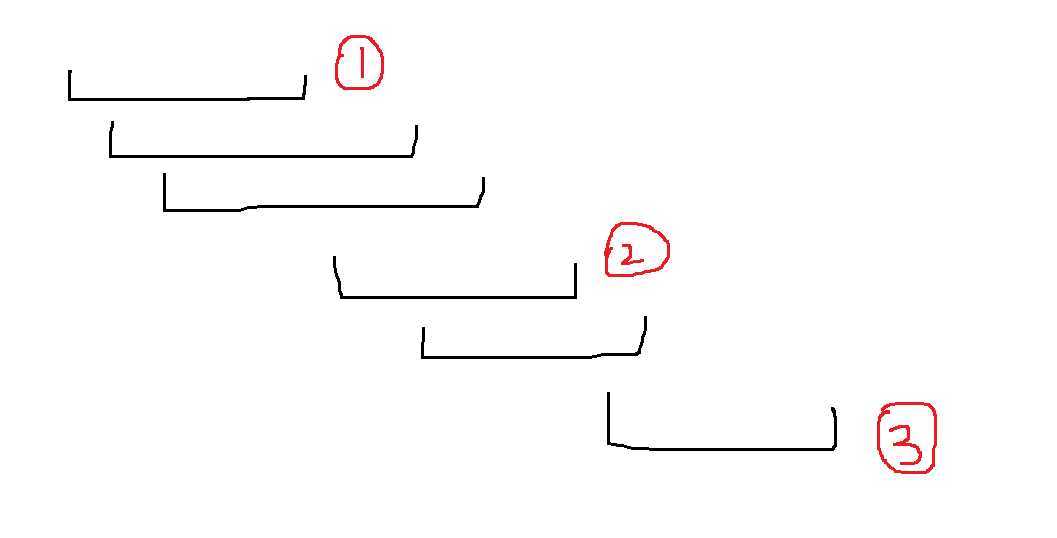
代码:
#include<iostream> #include<cmath> #include<cstdio> #include<algorithm> using namespace std; const int N=10101; struct node { double l,r; bool operator <(const node &t)const { return r<t.r; } }s[N]; int main() { int i,j,n,d,x,y; bool flag=false; scanf("%d%d",&n,&d); for(i=0;i<n;i++) { scanf("%d%d",&x,&y); if(y>d) flag=true; else { double len=sqrt(d*d-y*y); s[i].l=x-len;s[i].r=x+len;//计算每个岛的区间 } } if(flag==true) { puts("-1"); } else { sort(s,s+n);//按照区间右端点排序 int cnt=0; double nowl=-1e20; for(i=0;i<n;i++) { if(nowl<s[i].l)//判断当前取件是否有下一个区间的点 { cnt++; nowl=s[i].r;//更新区间 } } printf("%d\n",cnt); } return 0; }
2.付账问题
题目链接:https://www.acwing.com/problem/content/1237/
解题思路:计算最小的方差,S是固定的,因此AVG也是固定的,只要每个人所掏的钱数越接近于AVG,那么方差就会越小
①首先如果每个人的钱数都超过AVG,那么方差就是0
②如果有的人可能钱包小于AVG,那么不够的钱应该分摊到那些钱包有剩余的人那里,因此,我们首先需要将每个人的钱进行从小到大排序,分别计算当前人数的平均值,看当前这个人的钱包是否足够,不够就掏出自己目前所有的钱,然后,到第二个人的时候需要掏的钱:(S-a[0])/(n-1),如果也不够,也是掏出自己目前所有的钱,到第三个人的时候需要掏出:(S-a[0]-a[1])/(n-2)依次类推,算出最小方差,进而算出最小标准差,再保留4为小数。
代码:
#include<iostream> #include<cmath> #include<cstdio> #include<algorithm> using namespace std; const int N=500010; int n,a[N]; double s; int main() { int i,j; cin>>n>>s; for(i=0;i<n;i++) cin>>a[i]; sort(a,a+n); double ans=0,avg=s/n; for(i=0;i<n;i++) { double cur=s/(n-i); if(a[i]<cur) cur=a[i]; ans+=(cur-avg)*(cur-avg); s-=cur; } printf("%.4lf",sqrt(ans/n)); return 0; }
3.乘积最大
题目链接:https://www.acwing.com/problem/content/description/1241/
解题思路:双指针算法,根据K的奇偶分别计算
当K是偶数,结果非负,因为,如果负数是偶数个,负负得正,结果为非负;如果负数是奇数个,那就选偶数个绝对值最大的负数
k 如果是奇数个的话,
(1)所有的数字如果都是负数,那么选出来的结果也一定都是负数
(2)否则的话,则一定至少有 1个非负数, 那么我们将最大的数取出来, 此时要选的个数就是 k--,
# k-- 是偶数,那么就又转化为 k-- 是偶数的情况思考
代码:
#include<iostream> #include<algorithm> #include<cstdio> using namespace std; typedef long long ll; int n,k; const int mod=1000000009; const int N=100010; int a[N]; int main() { int i,j; cin>>n>>k; for(i=0;i<n;i++) cin>>a[i]; sort(a,a+n); ll res=1,l=0,r=n-1; int sign=1; if(k%2) { res=a[r--]; k--; if(res<0) sign=-1; } while(k) { ll x=(ll)a[l]*a[l+1]; ll y=(ll)a[r]*a[r-1]; if(x*sign>y*sign) { res=x%mod*res%mod; l+=2; } else { res=y%mod*res%mod; r-=2; } k-=2; } printf("%lld",res); return 0; }
原文:https://www.cnblogs.com/xiaofengzai/p/13166666.html