Structure Boundary Preserving Segmentation for Medical Image With Ambiguous Boundary（理解）

原文链接传送门

扫码关注下方公众号："Python编程与深度学习"，领取配套学习资源，并有不定时深度学习相关文章及代码分享。

今天分享一篇发表在CVPR2020上的关于医学图像处理的论文：Structure Boundary Preserving Segmentation for Medical Image With Ambiguous Boundary (论文链接)。

1 研究背景

当前医学影像分割任务存在两个关键问题：

• 分割区域边界的模糊性
• 缺乏专业领域知识的前提下分割区域的不确定性

这篇文章针对上述问题提出了解决方案，主要有如下三点贡献：

• 提出一种新颖的边界关键点选择算法（boundary key point selection algorithm），使得能够用关键点来表示分割目标域的结构边界（解决上述第一个问题）
• 提出了一个新颖的结构边界保持(structure boundary preserving segmentation)分割框架，并且使得模型能够自动提取和学习结构关键点信息而不需要医生的交互（解决上述第二个问题）
• 文中提出的分割框架可以应用到不同分割模型上，并且作者做了足够的实验进行验证

文中的模型效果如下图，相比于U-Net，作者提出的模型能够更好的处理分割区域的边界。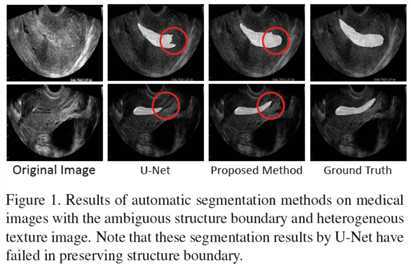

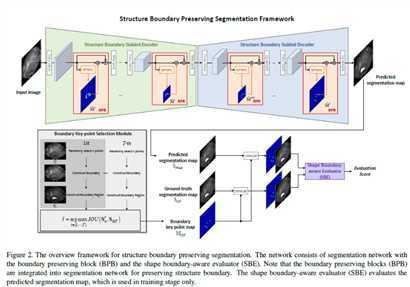
2 方法

2.1 整体流程

如上图（Figure 2）所示，整个模型可以分解为三个主要部分：分割网络、边界保持模块(Boundary Preserving Block, BPB)以及形状边界判别器(Shape Boundary-aware Evaluator, SBE)。

分割网络: 可以由流行的语义分割网络构成，例如U-Net等。

边界保持模块: 该模块能够嵌入到卷积网络中，其思想是在卷积模块中，根据其输入特征产生对应的边界点图，而后将边界点图融入到下一个卷积模块的特征输入中，同时边界点图做一个监督学习。（感觉有点类似中间监督+注意力机制）

形状边界判别器： 模型最终产生的分割图预测与中间卷积模块中产生的边界点图可以通过形状边界判别器来约束它们之间表达的一致性。

这篇文章的创新主要在于边界保持模块和形状边界判别器，后面将主要对这两个模块进行介绍。

2.2 边界关键点选择算法(Boundary Key Point Selection Algorithm)

由于文中采用边界关键点来表示目标边界，因此在介绍边界保持模块之前，需要先了解怎么选择边界关键点。文中边界关键点选择算法的具体过程是：

1. 采用常规边界检测算法[2]获取标签分割图上目标区域的边界
2. 在目标区域的边界上随机选取$n$个点组成点集，用$P_n^t=\{(x_1^t,y_1^t),(x_2^t,y_2^t),\cdots,(x_n^t,y_n^t)\}$来表示，其中$t$表示迭代的轮数
3. 然后将$P_n^t$中的点连接起来围成边界区域，用$S_n^t=c(P_n^t)$表示
4. 而后选择$t$次迭代中边界区域$S_n^t$与标签分割图$S_{GT}$具有最大IOU(Intersection Over Union)的点集作为结构边界关键点集，可以用下面公式进行表示：
   $$\tilde{P}=P_n^{\tilde{t}}, where\ \tilde{t}=argmax_{t\in\{1,\cdots,T\}}IOU(S_n^t,S_{GT})$$
5. 结构边界关键点集$\tilde{P}$表示的是图中的一个一个位置，为了能够更加适合处理图像的卷积网络训练，文中采用2D的边界点图(boundary point map)来表示这些点。具体地，边界点图中是以这些点为中心，将它们周围半径为$R$的区域内都置为1，其余位置置为0。（提示：边界点图的构造方式类似关键点检测任务中heatmap的构造方法，这种做法的好处在于2D的表示更适合卷积网络的训练和预测）

上述的过程写成算法形式就如Algorithm 1所示：

2.3 边界保持模块(Boundary Preserving Block, BPB)

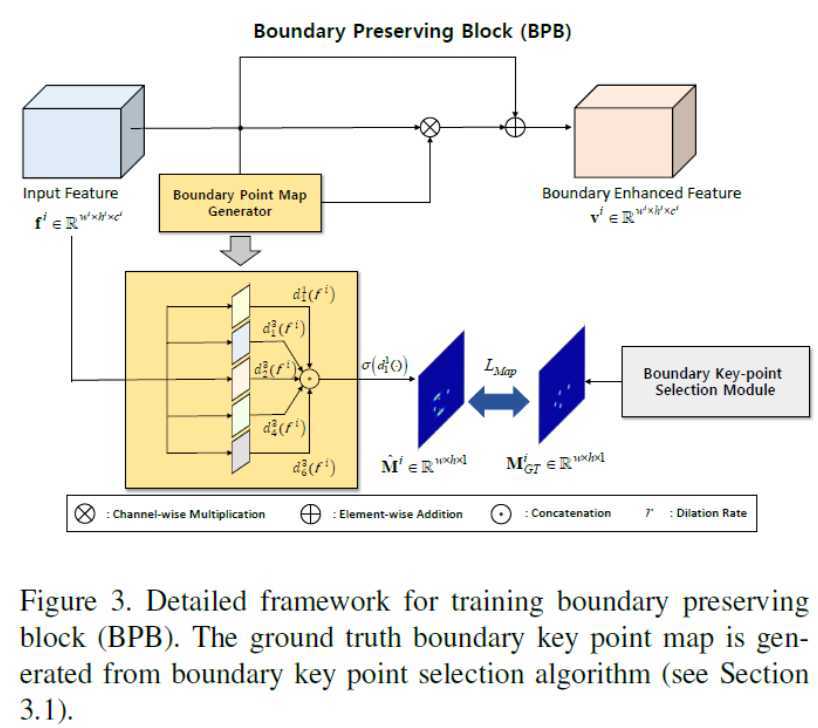
上图（Figure 3）展示了如何在卷积网络中嵌入BPB模块，以达到在预测分割图的过程中将边界关键点考虑进去。具体地，假设现在是第$i$个卷积模块，模块的输入特征维度为$f^i\in \mathbf{R}^{w^i\times h^i\times c^i}$，BPB的过程为：

1. 采用上述算法生成对应该模块的边界点图$\hat{M}^i\in\mathbf{R}^{w^i\times h^i\times 1}$
2. 然后将输入特征$f^i$和$\hat{M}^i$做元素点乘（$\hat{M}^i$在第三维度上需要广播），而后将结果和输入特征$f^i$进行相加，得到结构边界信息保持特征$v^i\in \mathbf{R}^{w^i\times h^i\times c^i}$作为输出特征。

这个过程可写成如下公式：
$$v^i=f^i\oplus(f^i \otimes \hat{M}^i)$$

Figure 3中需要注意的还有$\hat{M}^i$的生成过程，将并行的多路空洞卷积(the dilated convolution)产生的特征连接起来，再进一步做边界点图的预测，用公式表达如下：
$$\hat{M}^i=\sigma\left (d_1^1\{[d_1^1(f^i),d_1^3(f^i),d_2^3(f^i),d_4^3(f^i),d_6^3(f^i)]\}\right )$$
其中$d_r^s(f^i)$表示空洞率(dilation rate)为$r$，卷积核大小为$s\times s$的空洞卷积函数(dilated convolution function)。

2.4 形状边界判别器(Shape Boundary-aware Evaluator, SBE)

采用上述的BPB模块嵌入到卷积网络中其实已经可以达到结构边界保持的目的了，但可能存在问题：模型预测的边界点图和模型预测的分割区域可能不是很匹配，比如某一些点虽然在边界点图预测正确了，但最终预测却缺失了。为了解决这个问题，文中提出了SBE，SBE是一个二分类器，其输入是边界点图和分割图，输出为一致性分数，高分即一致，低分则不一致。我的理解是相当于在预测边界点图和预测分割图之间加了约束，使得模型能够产生更优质的预测结果。

2.5 损失函数

综合上述的分析，文中提出的模型会产生3个部分的预测：分割图预测、各个卷积模块对应的边界点图预测、SBE的预测。因此损失函数由这三部分的损失函数组成，表示为：
$$L_{Total}=L_{Seg}+L_{BA}+\sum_{i=1}^lL_{Map}^i$$
其中$L_{Seg}$为预测的分割图的损失函数：
$$L_{Seg}=-S_{GT}\cdot log\left (\hat{S}_{Pred}\right )-(1-S_{GT})\cdot log\left (1-\hat{S}_{Pred}\right )$$
$L_{Map}^i$表示预测的边界点图的损失函数：
$$L_{Map}^i=-M_{GT}^i\cdot log\hat{M}^i-(1-M_{GT}^i)\cdot log(1-\hat{M}^i)$$
$L_{BA}$为作用在SBE预测结果上的损失函数：
$$L_{BA}=-log\left(D(\hat{S}_{Pred};M_{GT}) \right)$$
其中$D(\cdot)$表示SBE接收分割图和边界点图作为输入并产生预测分数。

3 实验结果

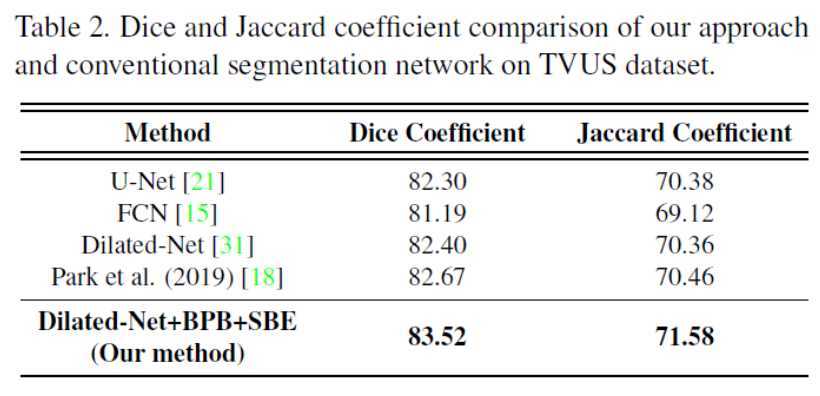
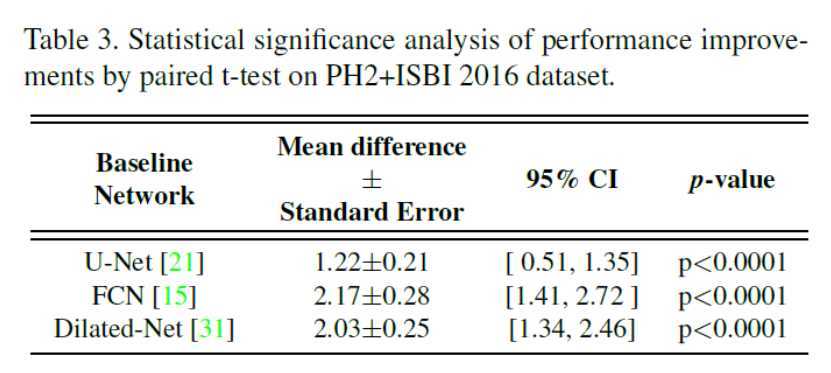
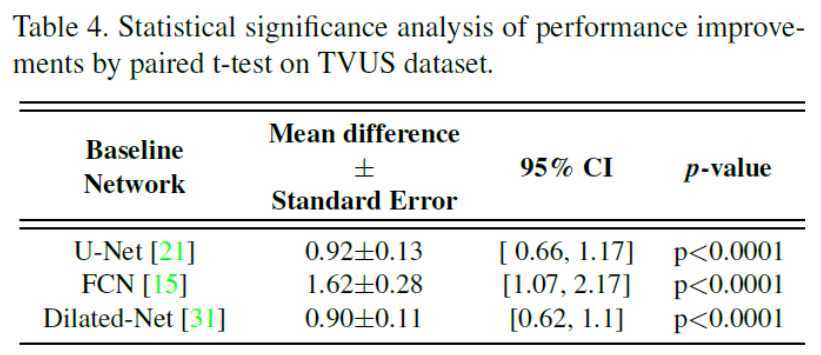
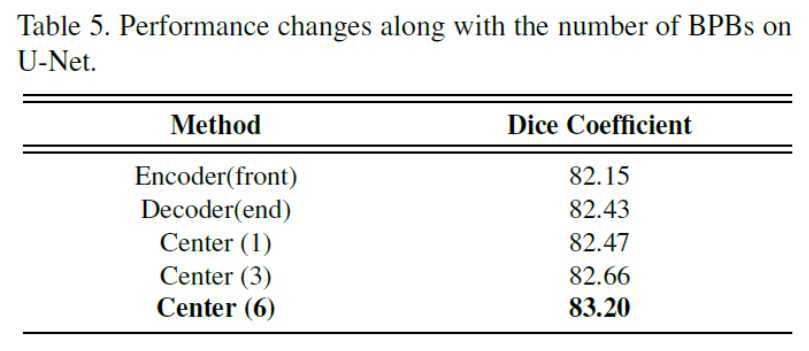
这里我只给出论文中的定量和定性分析的表格或者图片，具体的结果分析可以看原文。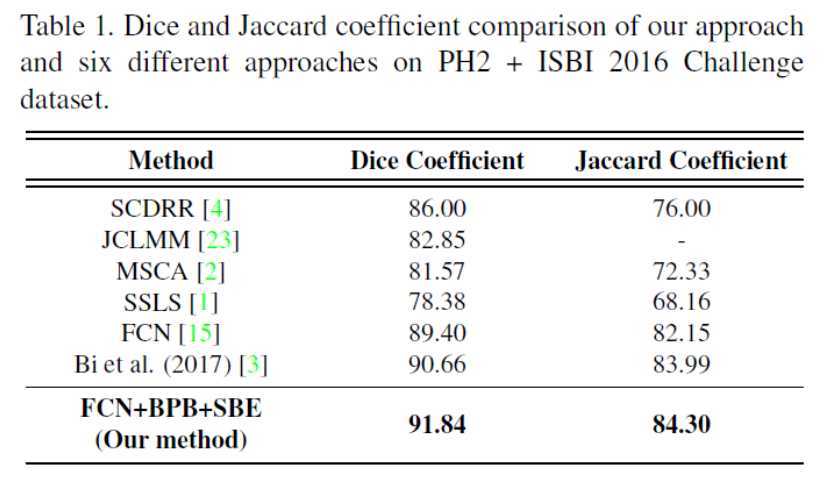

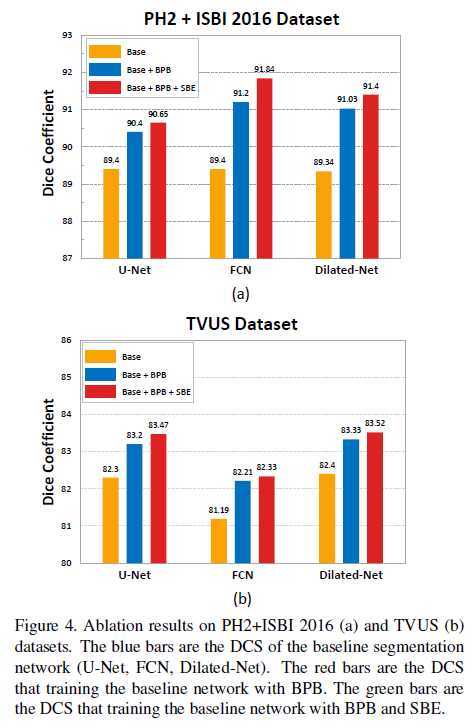
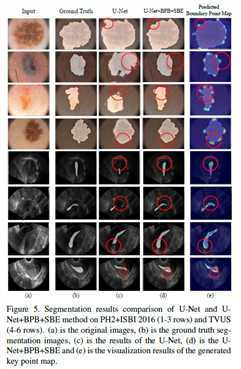
 4 参考资料

[1] http://openaccess.thecvf.com/content_CVPR_2020/papers/Lee_Structure_Boundary_Preserving_Segmentation_for_Medical_Image_With_Ambiguous_Boundary_CVPR_2020_paper.pdf

[2] John Canny. A computational approach to edge detection. IEEE Transactions on pattern analysis and machine intelligence, (6):679–698, 1986. 4

Structure Boundary Preserving Segmentation for Medical Image With Ambiguous Boundary（理解）

原文：https://www.cnblogs.com/CZiFan/p/13168977.html