红黑树的特点

先说平衡二叉树（AVLTree）:

作用：就是查找，AVL树的查找，插入和删除再平均和最坏情况下都是O（logn）。如果再AVL树中插入或删除节点后，使得高度之差大于1.此时AVL树的平衡状态就被破坏，他就不是一颗平衡二叉树。如果要它维持在一个平衡状态，就需要对其进行旋转处理，那么创建一颗二叉树的成本其实不小。就有人提出了红黑树理论，那么红黑树到底比AVL树好在哪里？

• 红黑树与AVL树的比较：
  1. AVL树的时间复杂度虽然由于红黑树，但是对于现在的计算机，cpu太快，可以忽略性能差异。
  2. 红黑树的插入删除比AVL树更便于控制操作。
  3. 红黑树整体性能略优于AVL树。（红黑树旋转情况少于AVL树）
• 红黑树的性质：（时间复杂度o(lgn)）
  • 每个节点不是黑色就是红色
  • 根节点是黑色的。
  • 如果一个节点是红色，那么他的俩个子节点就是黑色
  • 对于每个节点，从该节点到其后代叶结点的简单路径上包含相同数目的黑色节点。
• 如何保证最长路路径不超过最短路径的俩倍呢？
  • 
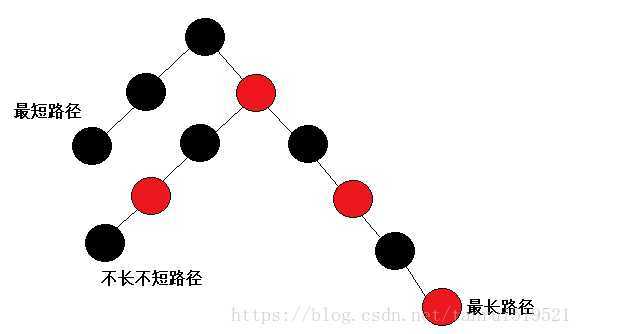
  • 最短路径：全是黑节点；最长路径：黑白相间。-----》所以当最长路径黑色节点数目同最短路径黑色节点相同时，最长路径恰好是最短路径的俩倍。
  • 颜色表示：因为每个结点都只会有一条指向自己的链接（从它的父结点指向它），我们将链接的颜色保存在表示结点的Node数据类型的布尔变量color中（若指向它的链接是红色的，那么该变量为true，黑色则为false）。当我们提到一个结点颜色时，我们指的是指向该结点的链接的颜色。

参考：https://blog.csdn.net/yang_yulei/article/details/26066409?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase

https://blog.csdn.net/tanrui519521/article/details/80980135?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase

红黑树的特点

原文：https://www.cnblogs.com/jibisheng/p/13178619.html