Q:给定两个单词(beginWord 和 endWord)和一个字典 wordList,找出所有从 beginWord 到 endWord 的最短转换序列。转换需遵循如下规则:
每次转换只能改变一个字母。
转换后得到的单词必须是字典中的单词。
说明:
如果不存在这样的转换序列,返回一个空列表。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的,且二者不相同。
示例 1:
输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
输出:
[
["hit","hot","dot","dog","cog"],
? ["hit","hot","lot","log","cog"]
]
示例 2:
输入:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
输出: []
解释:?endWord "cog" 不在字典中,所以不存在符合要求的转换序列。
A:
看到找出所有路径的,第一反应肯定是DFS回溯,但这个题又有一个条件,就是找最短路径,这实际上符合BFS。又由于知道开始和结束,所以可以用双向BFS
为方便剪枝,可用DFS结合BFS解决问题。
文中思路部分引用自详细通俗的思路分析,多解法
1.第一反应写的回溯法,但超时了
private List<List<String>> result;
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
List<String> list = new ArrayList<>();
result = new ArrayList<>();
if (!wordList.contains(endWord)) {
return result;
}
boolean[] visited = new boolean[wordList.size()];
Arrays.fill(visited, false);
list.add(beginWord);
help(list, beginWord, endWord, wordList, visited);
return result;
}
private void help(List<String> list, String currWord, String target, List<String> wordList, boolean[] visited) {
if (currWord.equals(target)) {
if (result.isEmpty())
result.add(new ArrayList<>(list));
else {//只加最短的
if (result.get(0).size() > list.size()) {
result.clear();
result.add(new ArrayList<>(list));
} else if (result.get(0).size() == list.size()) {
result.add(new ArrayList<>(list));
}
}
return;
}
//list已经比最短的长了
if (!result.isEmpty() && result.get(0).size() <= list.size())
return;
//对workList里面每个string进行判断
for (int i = 0; i < wordList.size(); i++) {
if (!visited[i] && oneChange(currWord, wordList.get(i))) {
list.add(wordList.get(i));
visited[i] = true;
help(list, wordList.get(i), target, wordList, visited);
visited[i] = false;
list.remove(list.size() - 1);
}
}
}
private boolean oneChange(String currWord, String newWord) {
int count = 0;
for (int i = 0; i < currWord.length(); i++) {
if (currWord.charAt(i) != newWord.charAt(i))
count++;
}
return count == 1;
}
2.进行回溯时,不是把整个wordList都放进去,而是把当前word的邻居放入一个list后再进行回溯。计算邻居时将要找的节点单词的每个位置换一个字符,然后看更改后的单词在不在 wordList 中。
private List<List<String>> result;
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
List<String> list = new ArrayList<>();
result = new ArrayList<>();
if (!wordList.contains(endWord)) {
return result;
}
list.add(beginWord);
help(list, beginWord, endWord, wordList);
return result;
}
private void help(List<String> list, String currWord, String target, List<String> wordList) {
if (currWord.equals(target)) {
if (result.isEmpty())
result.add(new ArrayList<>(list));
else {//只加最短的
if (result.get(0).size() > list.size()) {
result.clear();
result.add(new ArrayList<>(list));
} else if (result.get(0).size() == list.size()) {
result.add(new ArrayList<>(list));
}
}
return;
}
//list已经比最短的长了
if (!result.isEmpty() && result.get(0).size() <= list.size())
return;
List<String> neighbors = neighbors(list, currWord, wordList);
for (String n : neighbors) {
list.add(n);
help(list, n, target, wordList);
list.remove(list.size() - 1);
}
}
private List<String> neighbors(List<String> list, String currWord, List<String> wordList) {
List<String> neighbor = new ArrayList<>();
Set<String> l = new HashSet<>(list);
Set<String> w = new HashSet<>(wordList);
char[] curr = currWord.toCharArray();
for (int i = 0; i < curr.length; i++) {
char old = curr[i];
for (char c = ‘a‘; c <= ‘z‘; c++) {
if (c == old)
continue;
curr[i] = c;
String newWord = new String(curr);
if (!l.contains(newWord) && w.contains(newWord))
neighbor.add(newWord);
}
curr[i] = old;
}
return neighbor;
}
还是超时了。
3.DFS结合BFS
如图,在 BFS 的过程中,把第一次遇到的单词当前的层数存起来。之后遇到也不进行更新,就会是下边的效果。
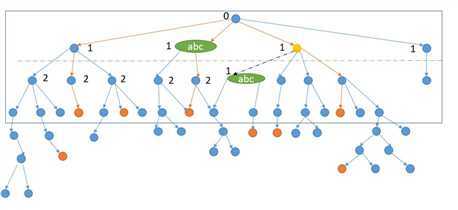
实际上,我们就是减少了第三层的 abc 的情况的判断。我们其实可以不用 distance ,在 BFS 中,如果发现有邻接节点在之前已经出现过了,我们直接把这个邻接节点删除不去。这样的话,在 DFS 中就不用再判断了,直接取邻居节点就可以了。
判断之前是否已经处理过,可以用一个 HashSet 来把之前的节点存起来进行判断
private List<List<String>> result;//放最后结果
private HashMap<String, List<String>> map;//放每个节点及其neighbors
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
result = new ArrayList<>();
if (!wordList.contains(endWord))
return result;
map = new HashMap<>();
// 利用 BFS 得到所有的邻居节点
bfs(beginWord, endWord, wordList);
// temp 用来保存当前的路径
List<String> temp = new ArrayList<>();
temp.add(beginWord);
findHelper(beginWord, endWord, temp);//DFS
return result;
}
private void findHelper(String currWord, String target, List<String> temp) {
if (currWord.equals(target)) {
result.add(new ArrayList<>(temp));
return;
}
List<String> neighbors = map.getOrDefault(currWord, new ArrayList<>());
for (String neighbor : neighbors) {
temp.add(neighbor);
findHelper(neighbor, target, temp);
temp.remove(temp.size() - 1);
}
}
private void bfs(String beginWord, String endWord, List<String> wordList) {
Queue<String> queue = new LinkedList<>();
queue.offer(beginWord);
boolean isFound = false;
Set<String> dict = new HashSet<>(wordList);
Set<String> visited = new HashSet<>();
visited.add(beginWord);
while (!queue.isEmpty()) {
int size = queue.size();
//存当前层的访问过的下一层,用这个是防止后面一层有同样的neighbor
Set<String> subVisited = new HashSet<>();
for (int j = 0; j < size; j++) {
String temp = queue.poll();
List<String> neighbors = getNeighbors(temp, visited, dict);//当前层或前层存在过就不用再读了
for (String neighbor : neighbors) {
if (neighbor.equals(endWord))
isFound = true;//已经找到这层有结果了,可以跳出去,不用再往后面找了
subVisited.add(neighbor);
queue.offer(neighbor);
}
map.put(temp, neighbors);//把当前点及其下层点放入
}
visited.addAll(subVisited);
if (isFound)
break;
}
}
private List<String> getNeighbors(String curr, Set<String> visited, Set<String> dict) {
List<String> res = new ArrayList<>();
char[] chs = curr.toCharArray();
for (char c = ‘a‘; c <= ‘z‘; c++) {
for (int i = 0; i < chs.length; i++) {
char old = chs[i];
if (c == old)
continue;
chs[i] = c;
String newWord = new String(chs);
if (!visited.contains(newWord) && dict.contains(newWord)) {
res.add(newWord);
}
chs[i] = old;
}
}
return res;
}
4.直接摒弃DFS,用BFS,一边进行层次遍历,一边就保存结果。当到达结束单词的时候,就把结果存储。省去再进行 DFS 的过程。是完全可以的,BFS 的队列就不去存储 String 了,直接去存到目前为止的路径,也就是一个 List。
private List<List<String>> result;
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
result = new ArrayList<>();
if (!wordList.contains(endWord))
return result;
bfs(beginWord, endWord, wordList);
return result;
}
private void bfs(String beginWord, String endWord, List<String> wordList) {
Queue<List<String>> queue = new LinkedList<>();//queue里存的是路径
List<String> path = new ArrayList<>();
path.add(beginWord);
queue.add(path);
boolean isFound = false;
Set<String> dict = new HashSet<>(wordList);
Set<String> visited = new HashSet<>();
visited.add(beginWord);
while (!queue.isEmpty()) {
int size = queue.size();
Set<String> subVisited = new HashSet<>();//当前层的neighbor
for (int i = 0; i < size; i++) {
List<String> p = queue.poll();
String curr = p.get(p.size() - 1);//路径最后一个是当前层的值
List<String> neighbors = getNeighbors(curr, visited, dict);
for (String neighbor : neighbors) {
List<String> newPath = new ArrayList<>(p);
newPath.add(neighbor);//路径更新
if (neighbor.equals(endWord)) {//BFS已经找到当前最短层了
isFound = true;
result.add(newPath);
}
subVisited.add(neighbor);
queue.add(newPath);
}
}
visited.addAll(subVisited);
if (isFound)
break;
}
}
private List<String> getNeighbors(String curr, Set<String> visited, Set<String> dict) {
List<String> res = new ArrayList<>();
char[] chs = curr.toCharArray();
for (char c = ‘a‘; c <= ‘z‘; c++) {
for (int i = 0; i < chs.length; i++) {
char old = chs[i];
if (c == old)
continue;
chs[i] = c;
String newWord = new String(chs);
if (!visited.contains(newWord) && dict.contains(newWord)) {
res.add(newWord);
}
chs[i] = old;
}
}
return res;
}
5.知道开头,知道结尾,可以用双向BFS
我们可以从结束单词反向进行 BFS。
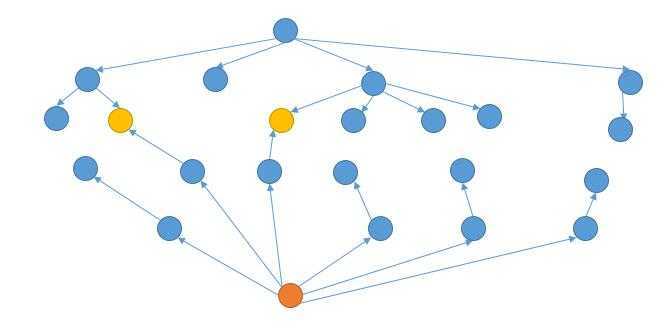
这样的话,当两个方向产生了共同的节点,就是我们的最短路径了。
至于每次从哪个方向扩展,我们可以每次选择需要扩展的节点数少的方向进行扩展。
例如上图中,一开始需要向下扩展的个数是 1 个,需要向上扩展的个数是 1 个。个数相等,我们就向下扩展。然后需要向下扩展的个数就变成了 4 个,而需要向上扩展的个数是 1 个,所以此时我们向上扩展。接着,需要向上扩展的个数变成了 6 个,需要向下扩展的个数是 4 个,我们就向下扩展......直到相遇。
双向扩展的好处,我们粗略的估计一下时间复杂度。假设 beginword 和 endword 之间的距离是 d。每个节点可以扩展出 k 个节点。那么正常的时间复杂就是 \(k^d\)。双向搜索的时间复杂度就是 \(k^{d/2} + k^{d/2}\)
(借鉴的引用文章代码)
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
List<List<String>> ans = new ArrayList<>();
if (!wordList.contains(endWord)) {
return ans;
}
// 利用 BFS 得到所有的邻居节点
HashMap<String, ArrayList<String>> map = new HashMap<>();
bfs(beginWord, endWord, wordList, map);
ArrayList<String> temp = new ArrayList<String>();
// temp 用来保存当前的路径
temp.add(beginWord);
findLaddersHelper(beginWord, endWord, map, temp, ans);
return ans;
}
private void findLaddersHelper(String beginWord, String endWord, HashMap<String, ArrayList<String>> map,
ArrayList<String> temp, List<List<String>> ans) {
if (beginWord.equals(endWord)) {
ans.add(new ArrayList<String>(temp));
return;
}
// 得到所有的下一个的节点
ArrayList<String> neighbors = map.getOrDefault(beginWord, new ArrayList<String>());
for (String neighbor : neighbors) {
temp.add(neighbor);
findLaddersHelper(neighbor, endWord, map, temp, ans);
temp.remove(temp.size() - 1);
}
}
//利用递归实现了双向搜索
private void bfs(String beginWord, String endWord, List<String> wordList, HashMap<String, ArrayList<String>> map) {
Set<String> set1 = new HashSet<String>();
set1.add(beginWord);
Set<String> set2 = new HashSet<String>();
set2.add(endWord);
Set<String> wordSet = new HashSet<String>(wordList);
bfsHelper(set1, set2, wordSet, true, map);
}
// direction 为 true 代表向下扩展,false 代表向上扩展
private boolean bfsHelper(Set<String> set1, Set<String> set2, Set<String> wordSet, boolean direction,
HashMap<String, ArrayList<String>> map) {
//set1 为空了,就直接结束
//比如下边的例子就会造成 set1 为空
/* "hot"
"dog"
["hot","dog"]*/
if(set1.isEmpty()){
return false;
}
// set1 的数量多,就反向扩展
if (set1.size() > set2.size()) {
return bfsHelper(set2, set1, wordSet, !direction, map);
}
// 将已经访问过单词删除
wordSet.removeAll(set1);
wordSet.removeAll(set2);
boolean done = false;
// 保存新扩展得到的节点
Set<String> set = new HashSet<String>();
for (String str : set1) {
//遍历每一位
for (int i = 0; i < str.length(); i++) {
char[] chars = str.toCharArray();
// 尝试所有字母
for (char ch = ‘a‘; ch <= ‘z‘; ch++) {
if(chars[i] == ch){
continue;
}
chars[i] = ch;
String word = new String(chars);
// 根据方向得到 map 的 key 和 val
String key = direction ? str : word;
String val = direction ? word : str;
ArrayList<String> list = map.containsKey(key) ? map.get(key) : new ArrayList<String>();
//如果相遇了就保存结果
if (set2.contains(word)) {
done = true;
list.add(val);
map.put(key, list);
}
//如果还没有相遇,并且新的单词在 word 中,那么就加到 set 中
if (!done && wordSet.contains(word)) {
set.add(word);
list.add(val);
map.put(key, list);
}
}
}
}
//一般情况下新扩展的元素会多一些,所以我们下次反方向扩展 set2
return done || bfsHelper(set2, set, wordSet, !direction, map);
}
原文:https://www.cnblogs.com/xym4869/p/13139911.html