反向图

之前学过一些单源最短路算法，跑得非常快，但是对于SPFA这个东东，虽然它出过幺蛾子，但是在题解区发现还是很多人用，但是今天自己在做题的时候发现它还是有用，呼吁大家最好还是学学，不要有啥偏见，虽然Dijkstra确实很香。直接用例题来讲

但是本蒟蒻对于反向图的了解还并不多，如果之后学到更多的东西会继续更新

P1629 邮递员送信

我们从一个点跑出去，然后出题人 像个睿智一样 还要再跑回起点之后才能去其他地方，这么一看，这不就是Floyd的吗，但是那个时间复杂度不敢想象，直接给你T飞

换个思路，对于每一次出去，我们跑一次单源最短路其实就够了，但是对于跑回来，我们就需要跑n次最短路，非常暴力，时间复杂度也不怎么样

#include <bits/stdc++.h>
using namespace std;
int n,m,u,v,w,tot,ans,sum[200010];
int dis[200010],vis[200010],head[200010];
priority_queue<pair<int,int> > shan;

struct node {
	int to,net,val;
} e[200010];

inline void add(int u,int v,int w) {
	e[++tot].val=w;
	e[tot].to=v;
	e[tot].net=head[u];
	head[u]=tot;
}

inline void dijkstra(int s) {
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	dis[s]=0;
	shan.push(make_pair(0,s));
	while(!shan.empty()) {
		int x=shan.top().second;
		shan.pop();
		if(vis[x]) continue;
		vis[x]=1;
		for(register int i=head[x];i;i=e[i].net) {
			int v=e[i].to;
			if(dis[v]>dis[x]+e[i].val) {
				dis[v]=dis[x]+e[i].val;
				shan.push(make_pair(-dis[v],v));
			}
		}
	}
}

int main() {
	scanf("%d%d",&n,&m);
	for(register int i=1;i<=m;i++) {
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);
	}
	for(register int i=2;i<=n;i++) {
		dijkstra(i);
		ans+=dis[1];
	}
	dijkstra(1);
	for(register int i=2;i<=n;i++) ans+=dis[i];
	printf("%d",ans);
	return 0;
}

只有40分，这个时候就可以建反向图啦

什么意思呢？我们对于跑出去的情况，一次最短路就够了，这个地方没什么好优化的，主要是从其他地方跑回来，这个时候就可以建反向图啦

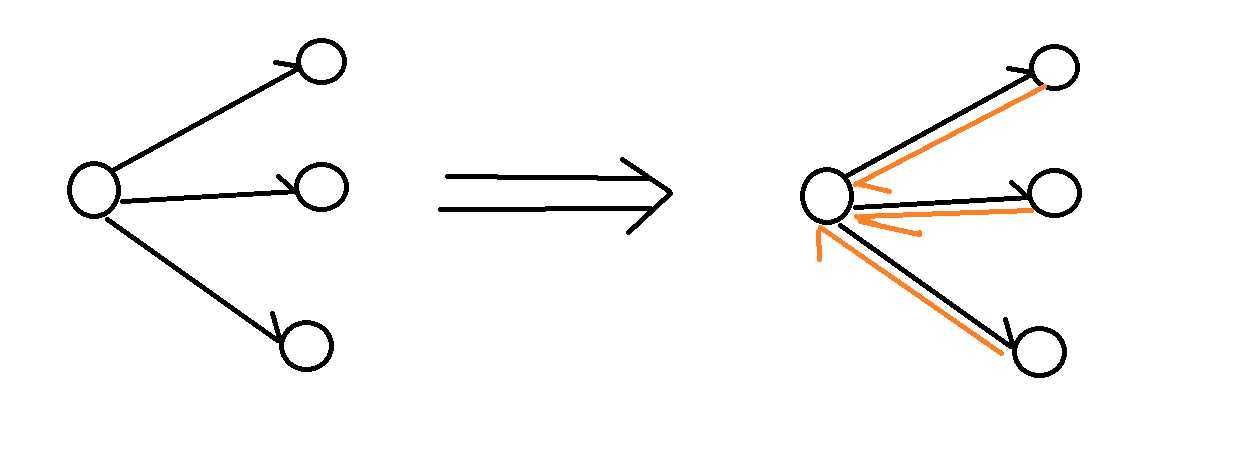
以下是一个正常的有向图，我们将所有边反转一下（多开一倍空间单独存储），但这里不是建双向边，是有区别的，不然想都不用想肯定出错，这样我们就可以在多的那一倍空间中处理回来的情况，把从别的地方回来也改为过去，就只需要跑一次最短路

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+50;
struct node {
	int to,net,w;
}e[2*MAXN];
int head[2*MAXN],tot;
void add(int u,int v,int w) {
	e[++tot].to=v;
	e[tot].net=head[u];
	head[u]=tot;
	e[tot].w=w;
}
int n,m,s;
int d[2*MAXN];
bool v[2*MAXN];
priority_queue< pair<int,int> > q;
void dij(int s){
	memset(d,0x3f,sizeof d);
	memset(v,false,sizeof v);
	d[s]=0;
	q.push(make_pair(0,s));
	while(!q.empty()){
		int x=q.top().second;
		q.pop();
		if(v[x]==true) continue;
		v[x]=true;
		for(register int i=head[x];i;i=e[i].net){
			int y=e[i].to,z=e[i].w;
			if(d[y]>d[x]+z){
				d[y]=d[x]+z;
				q.push(make_pair(-d[y],y));
			}
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(register int i=1;i<=m;i++){
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);
		add(v+n,u+n,w); //多开一倍空间处理反向边
	}
	dij(1);
	int ans=0;
	for(register int i=2;i<=n;i++) ans+=d[i]; //过去
	dij(1+n);
	for(register int i=n+1;i<=2*n;i++) ans+=d[i]; //回来
	cout<<ans;
	return 0;
}

又是一波三倍经验，爽啊！！！

P1342 请柬

SP50 INCARDS - Invitation Cards

对于反向图讲解目前就先到这里啦

反向图

原文：https://www.cnblogs.com/Poetic-Rain/p/13179080.html