前几天 弦中子 老师 在 反相吧 发了一个 帖 《快递员问题可否这样思考?》 https://tieba.baidu.com/p/6763029470 。
1 楼 提出了一个 “快递员问题” :
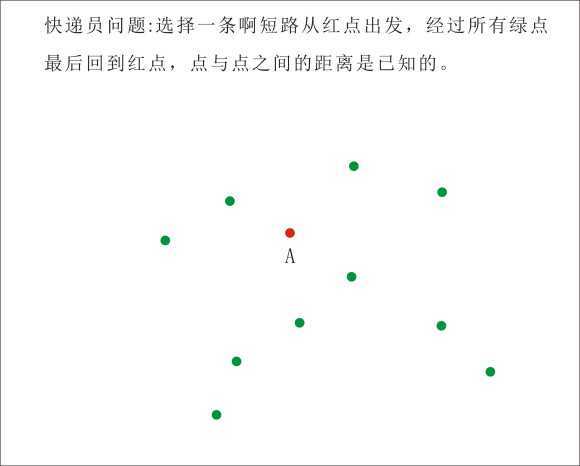
有一个快递员从家里出发,要经过n个点后回到家里,请问他走的最短路程是哪一条?
我 在 10 楼 这样回复 :
“
弦老师 的 这种 情况, 光 绝对 摸不着 头脑 该走 哪一个路径 是 “最近” 的 ,
那个 光, 估计 会 站在 那里 一直想 , 一直想 …… 于是 光速 为 0 了 。
假设 有 n 个 节点, 求 这些 节点 的 排列数量 = n ! , 每一个 排列 组成一条 路径, 计算 每一条 路径 的 长度, 排个序, 就知道 最短 的 路径 是 哪条 了 。
”
这里 引出 了 一个 排列组合 的 问题 。 排列 和 组合 都是 组合, 排列区分元素顺序, 组合不区分元素顺序, 比如 AB 和 BA 是 不同 的 排列, 是 同一个 组合 。
假设 有 ABCD 4 个 字母, 从中 拿出 2 个 字母 来 排列, 有多少种 排列 ? 排列考虑元素顺序, 不同的顺序算不同的排列 。
会有 4^2 = 4 * 4 = 16 种 排列 。 具体是
AA, AB, AC, AD
BA, BB, BC, BD
CA, CB, CC, CD
DA, DB, DC, DD
如果 是 从 ABCD 中 拿出 3 个 字母 来 排列, 则 会有 4^3 = 4 * 4 * 4 = 64 种 排列 。
这种 排列 允许 同一个 字母 在 一个 排列 中 重复使用, 比如 AA, BB, AAA, BBB, AAB, BBD 。
如果 不允许 同一个 字母 在 一个 排列 里 重复使用, 那么 从 ABCD 中 拿出 2 个 字母 来 排列, 有多少种 排列 ?
有 4 * 3 = 12 种 排列 。 具体是
AB, AC, AD
BA, BC, BD
CA, CB, CD
DA, DB, DC
从 ABCD 中 拿 3 个 字母 来 排列, 有 4 * 3 * 2 = 24 种 排列,
ABC ABD, ACB, ACD, ADB, ADC
BAC, BAD, BCA, BCD, BDA, BDC
CAB, CAD, CBA, CBD, CDA, CDB
DAB, DAC, DBA, DBC, DCA, DCB
从 ABCD 中 拿 4 个 字母 来 排列, 有 4 * 3 * 2 * 1 = 4 ! 种 排列, 这跟 上面 拿 3 个 字母 来 排列 是 一样 的,
ABCD ABDC, ACBD, ACDB, ADBC, ADCB
BACD, BADC, BCAD, BCDA, BDAC, BDCA
CABD, CADB, CBAD, CBDA, CDAB, CDBA
DABC, DACB, DBAC, DBCA, DCAB, DCBA
如果 把 ABCD 看作 4 个 点, 这 4 ! 种 排列 就是 把 4 个 点 连起来 可能 得到 的 路径, 就是 本文开头 的 快递问题 里 的 n 个点 可以 有 多少种 路径 。
原文:https://www.cnblogs.com/KSongKing/p/13193086.html