本章主要学习了查找的相关知识。关于查找,有以下几种基本概念:
(1)查找表。按照数据类型可分为数组和链表;按照具体存储逻辑又可分为顺序表、哈希表等等。
(2)关键字。作为待查找的元素,在查找表中进行检索。
(3)动态查找。若表中没有所查的关键字,则将关键字按照原表的规律添加在表中,形成一个含有关键字的新表。若只进行查找操作,而不插入关键字,则为静态查找。
(4)平均查找长度。查找表中值的平均比较次数。
二分查找:(1)前提:使用数组存储,存储的元素必须按升序或降序。
(2)平均比较次数:log2(n+1) 最坏比较次数 (int) log2(n)+1
散列表:使用某种特定的方法,将分散的数据压缩存储,将其所在的数组下标和存储内容建立联系。
目的:方便以后直接通过关键字,检索到其对应的位置。
构造散列表较为常用的方法:(1)平方取中法:将每个数据平方,再调取中间的几位数作为其数组下标。(2)除留余数法:规定一个数作为公除数,每一个需要存储的数据都进行求模,余数作为数组下标。
处理散列表冲突的方法:(1)线性探测法:发生冲突时,若数组内下一个元素为空,则直接填入下一数组元素内。(2)平方探测法:若产生冲突,则newH(key) = (H(key) ± i^2) % x, i={0,1,2,3,4...}。其中,x为给定的定值。
装填因子:存储元素个数/散列表大小
二叉搜索树:左子树的节点值均小于根节点的值,右子树的节点值均大于根节点的值。
最优二叉搜索树:最深层层数-最浅层层数<=1。
B、B+树:目的:面对大量数据,利用特定的检索方法,减少外部存储器和内存交换数据的次数,增加查找速度。
存储结构如图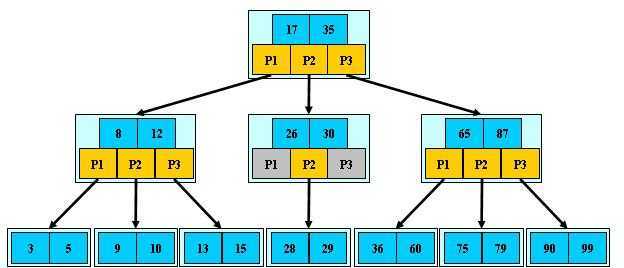
遇到的问题:在二分查找变形中,我将数组定义在了main函数中,导致程序段错误,原因是栈空间不足,后面将数组定义为全局变量,解决了这个问题。
1 #include <iostream> 2 using namespace std; 3 4 int a[1000000]; //将数组定义为全局变量 5 6 int search(int a[], int key, int low, int high); 7 8 int main(){ 9 ... 10 }
下一阶段的目标:更加深入理解掌握第七章的知识,临近期末,调整状态,拿出精力备考,在期末拿到一个好成绩。
原文:https://www.cnblogs.com/huyuehao/p/13196850.html