线段树（毒瘤）总结

我们在这篇博客里将具体介绍一种超级毒瘤超级高效的算法
线段树

概念引入

首先来认识一下线段树
什么是线段树呢：
线段树是一种二叉树，也就是对于一个线段，我们会用一个二叉树来表示。比如说一个长度为6的线段，我们可以表示成这样

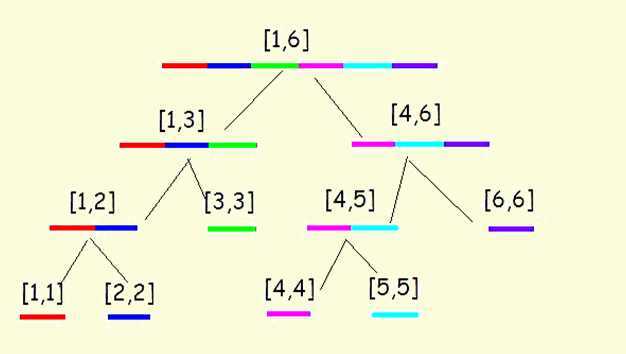
这个图是什么意思呢？

• 将这个做成一个树的结构 每个根节点存储左右两个节点的权值之和
  举个栗子:最上边的线段表示1～6的和 而他的左儿子表示1～3的和 右儿子表示4～6的和
• 然后他左儿子的左儿子又表示1～2的和 左儿子的右儿子表示3的权值
• 因此 节点i的权值=i左儿子的权值+i右儿子的权值
• 所以我们可以得到 tree[rt].sum = tree[l].sum + tree[r].sum
• 根据这个原理 我们就可以进行递归建树了

struct node{
      int l,r,sum;//l表示左儿子 r表示右儿子  sum表示当前节点存储的权值
}tree[maxn*4];

void build(int i,int l,int r){
	tree[i].l = l;tree[i].r = r;
	if(l == r){
		tree[i].sum = a[l];//a数组存储给出的数组初始值
		return;
	}
	int mid = (l+r)/2;
	build(i*2,l,mid);
	build(i*2+1,mid+1,r);
	tree[i].sum = tree[i*2].sum+tree[i*2+1].sum;
	return;
}

这就是线段树的建树方法 如果你要问为什么我们要花好几倍的内存去建树来完成一个数组就能完成的事情 那就是因为我们需要让这个超级大的数组去干一些比较困难的事情
那什么是比较困难的事情呢 让我们进入下个专题

简单的操作

单点修改 区间查询

• 举个例子 我们要求出区间1～5的和
• 显然可以 for(int i = 1;i<=5;++i){ans+=a[i]};
• 但是我们仍然要使用线段树来进行操作
• 首先看区间的位置
  当前处在根节点 存储的左边界是1 右边界是6
  根节点的左儿子的左边界是1 右边界是3 右儿子的左边界是4 右边界是6
  左儿子的区间完全被该区间包括 所以我们直接返回左儿子的权值
  右儿子的左边界在目标区间右边界的左边 所以我们继续递归搜索右边界
  现在最新的左儿子为4～5 完全包括在目标区间之中 直接返回权值 右儿子6与该区间毫无关系 返回0
  现在我们就可以把返回的值加起来了 3+2=5
• 有人可能会吐槽了 用一个数组能解决的问题 为什么要搞的这么复杂
• 但是有的时候虽然数组很方便 但是他并不能满足我们的需求 ，O(n)的效率 ，有时候是无法令出题人快乐的， 这个时候就需要用到线段树了 O(\(log_n\))

因此用代码怎么实现呢 也很简单
先让我们总结一下线段树的查询方式：

• 如果当前区间完全被包括在目标区间之中，直接返回当前区间的权值
• 如果当前区间与目标区间毫无关系 直接返回 0
• 如果当前区间与目标区间有交叉 继续递归搜索左儿子和右儿子
  那我们就可以有这样的代码实现形式

int search(int rt,int l,int r){
	if(tree[rt].r < l ||tree[rt].l > r)return 0;
	if(tree[rt].l >= l && tree[rt].r <= r)return tree[rt].sum;
	int ans = 0;
	if(tree[rt*2].r >= l)ans += search(2*rt,l,r);
	if(tree[rt*2+1].l <= r)ans += search(2*rt+1,l,r);
	return ans;
}

?那单点修改呢
?这个相对就简单许多了

• 给出一个位置x 一个值k
• 如果我们要修改x位置的数 让他加上一个数k 我们就让树去递归寻找这个位置

void add(int rt,int x,int k){
	if(tree[rt].l == tree[rt].r){//到达叶子节点 说明找到该位置
		tree[rt].sum += k;
		return;
	}
	if(x <= tree[rt*2].r)add(rt*2,x,k); // 递归搜索左儿子
	else add(rt*2+1,x,k);//递归搜索右儿子
	tree[rt].sum = tree[rt*2].sum + tree[rt*2+1].sum;//重新将权值加和
	return;
}

区间修改单点查询

区间修改和单点查询的方法有很多
为了一会对pushdown的讲解 我们这里说一种比较便于下面理解的方法

区间修改和区间查询很像

• 不过区间查询的 ”如果当前区间完全包括在目标区间就返回当前区间的值“要改为将当前区间打上k标记
• 举个例子： 我们要把一个区间所有的数加上k
• 那就去递归搜索线段树 如果发现某个线段树的区间完全包括在目标区间中 那就将这个区间打上k标记
• 但是我们这里的建树就要有所不同了
• 因为我们的所有节点的初始值都会为0(为了便于记录标记k)

void build(int l,int r,int rt){
    tree[rt].num=0;
    tree[rt].l=l;
    tree[rt].r=r;
    if(l==r)
        return ;
    int mid=(r+l)/2;
    build(l,mid,rt*2);
    build(mid+1,r,rt*2+1);
}

void add(int rt,int l,int r,int k){
    if(tree[rt].l>=l && tree[rt].r<=r){
        tree[rt].num+=k;
        return ;
    }
    if(tree[rt*2].r>=l)
       add(rt*2,l,r,k);
    if(tree[rt*2+1].l<=r)
       add(rt*2+1,l,r,k);
}

单点查询可以去寻找这个节点 路上遇到的所有标记都要累加起来 最后再加上这个节点的初始值
用代码实现大概是这个样子

void search(int rt,int dis){
    ans+=tree[rt].num;
    if(tree[rt].l==tree[rt].r)
        return ;
    if(dis<=tree[rt*2].r)
        search(rt*2,dis);
    if(dis>=tree[rt*2+1].l)
        search(rt*2+1,dis);
}
    //主函数中
    printf("%d\n",ans+a[x]);//a[x]为目标位置的初始值

建议将上面的板子打熟再向下继续观看

区间修改与区间查询（pushdown and lazy）

前方高难
看到这样的题你或许会想 不就是上边那两种放在一起吗
但是如果你真的这样写完了代码你会发现 WA
为什么呢


先来回想一下刚才的操作：将区间加上标记 最终查询的时候去从上往下找 将标记累加最后再加上初始值


但是这样真的可以吗？


答案是否定的 原因很简单：如果你要求1～3区间的和 而你刚刚将3～5的区间加上标记 因为1～3并不包含3～5的标记 所以我们计算后的结果并不是加k之后的和 而是初始值的和


那如何解决这个问题呢？ 也很简单:只要将我们的标记k下放到i的儿子不就好了吗


所以我们的算法雏形就出来了（这也是线段树最毒瘤而且难调最具有魅力的地方）

• 首先我们在结构体中多定义一个变量lazy 用于记录标记 每次有加的操作的时候我们就加到lazy上
• 然后就是下放操作pushdown 用于将lazy下放到i的儿子节点中
• 所以通过简单的推理和归纳我们仍然有以下性质：
  ? 1. 如果当前区间完全被包含在目标区间中 则这个区间的权值 tree[rt].sum += k*(tree[rt].r - tree[rt].l + 1)
  ? 2. 如果当前区间与目标区间有交集但是并没有被完全覆盖 就下放懒惰标记
  ? 3. 下放之后分别对左儿子和右儿子进行相同的操作
• 最后仍然是按照tree[rt].sum = tree[rt2].sum + tree[rt2+1].sum向上更新
  因此代码实现就是

void pushdown(long long rt){
	if(tree[rt].lazy != 0){//如果当前区间已经被标记
		tree[rt*2].lazy += tree[rt].lazy;//下放到左儿子
		tree[rt*2+1].lazy += tree[rt].lazy;//下放到右儿子
		long long mid = (tree[rt].l + tree[rt].r)/2;
		tree[rt*2].sum += tree[rt].lazy*(mid - tree[rt*2].l + 1);//更新左儿子的值
		tree[rt*2+1].sum += tree[rt].lazy*(tree[rt*2+1].r - mid);//更新右儿子的值
		tree[rt].lazy = 0;//清空当前节点的懒惰标记
	}
	return;
}

void add(long long rt,long long l,long long r,long long k){
	if(tree[rt].l >= l && tree[rt].r <= r){//如果当前区间完全包含在目标区间直接更新并且标记懒惰标记
		tree[rt].sum += k*(tree[rt].r-tree[rt].l+1);//更新当前区间的权值
		tree[rt].lazy += k;//增加懒惰标记
		return;
	}
	pushdown(rt);//下放懒惰标记
	if(tree[rt*2].r >= l)add(rt*2,l,r,k);//递归更新左儿子
	if(tree[rt*2+1].l <= r)add(rt*2+1,l,r,k);//递归更新右儿子
	tree[rt].sum = tree[rt*2].sum+tree[rt*2+1].sum;//更新当前节点的权值
	return;
}

区间查询的时候和之前几乎一样 不同的是要进行懒惰标记的下放之后在累加

long long search(long long rt,long long l,long long r){
	if(tree[rt].l >= l && tree[rt].r <= r)return tree[rt].sum;//如果当前区间完全包含在目标区间内 直接返回当前区间的权值
	if(tree[rt].r < l || tree[rt].l > r)return 0;//如果当前区间和目标区间完全没有关系 直接返回0
	pushdown(rt);//下放懒惰标记
	long long s = 0;
	if(tree[rt*2].r >= l)s += search(rt*2,l,r);
	if(tree[rt*2+1].l <= r)s += search(rt*2+1,l,r);
	return s;//最后返回这个区间的和
}

线段树模型大概就是这个样子(线段树还是比较受出题人青睐的难道是因为难调？？)
附上练习攻略：
简单线段树建议用洛谷P3374【模板】树状数组1
????????洛谷P3368【模板】树状数组2练习板子
如果简单线段树没有问题了
可以去尝试一下：洛谷P3372【模板】线段树1
????????洛谷P3373【模板】线段树2
????????洛谷P6242【模板】线段树3

谢谢观看
点个关注>_<

线段树（毒瘤）总结

原文：https://www.cnblogs.com/2004-08-20/p/13197875.html