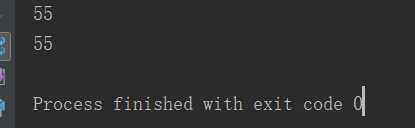
# 递归。重复计算,时间复杂度O(2^n)- O(1) ,空间复杂度为O(n) def fRecursive(n): if n == 0: return 0 elif n == 1: return 1 else: return fRecursive(n - 1) + fRecursive(n - 2) # a记录f(n-2)的值,b记录f(n-1)的值,不断更新a和b的值。非递归,空间复杂度O(1),时间复杂度O(n)。 def f(n): a, b, c, i = 0, 1, 1, 2 if n == 0: return 0 elif n == 1: return 1 else: while i <= n: c = a + b a = b b = c i = i + 1 return c if __name__ == "__main__": n = 10 print(fRecursive(n)) print(f(n))
原文:https://www.cnblogs.com/mydesky2012/p/13205049.html