Python_ML_19_EM算法

GMM跟EM没有直接相关性，只不过EM算法可以求解GMM的参数。

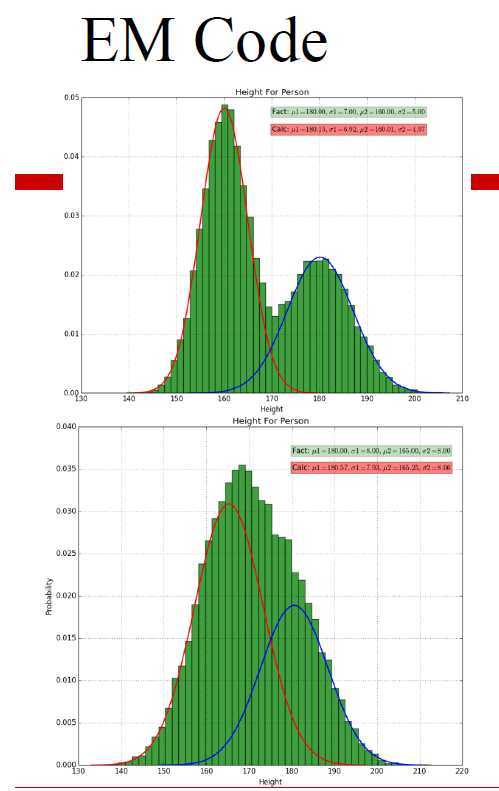
EM例子：给定人的身高数据，男性服从N（u₁，σ₁²），而女性服从N（u₂，σ₂²），aN（u₁，σ₁²）与（1-a）N（u₂，σ₂²）他们混在一起，假设得到了有1k个观测数据，算出u和σ的参数值。

若一个函数是凸函数，那么函数上有两个点x和y，他们之间的连线（割线）位于曲线的上方。它的不等式记为Jensen不等式：f(θx+(1-θ)y)<=θf(x)+(1-θ)f(y)。将Jensen不等式中θ改为θ1，而(1-θ)改为θ₂，不等式为：θ₁x₁+θ₂x₂ <=θ₁f(x₁)+θ₂f(x₂)。也可以将其改造成多个θ的不等式。

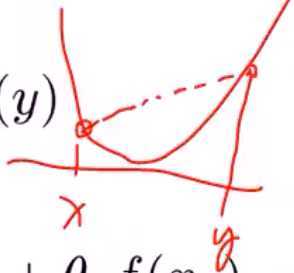
其中θ₁+θ₂+.. + θ_k = 1 可以看成是某个变量z的概率分布率P(z)。因此变量z，它的取值是1~k，它的概率是θ₁, θ₂.. θ_k ，那么不等式的左边就是θ₁*x₁+θ₂*x₂+.. + θ_k*x_k其实就是对x求期望：E(x)，然后对这个期望求 f 函数：f(E(x))。类似，右边的不等式是Ef(x)。所以最终的不等式是f(E(x))<=Ef(x)。

对于连续随机变量来说，也是同样的f(E(x))<=Ef(x)：f(∫p(x)xdx) <= ∫f(x)p(x)dx

Python_ML_19_EM算法

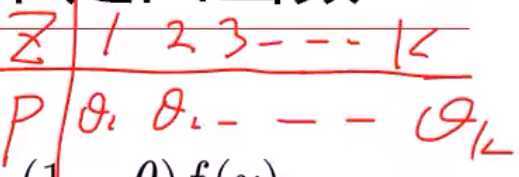
原文：https://www.cnblogs.com/tlfox2006/p/13206511.html